Negative 5 Minus Negative 4
scising
Sep 14, 2025 · 5 min read
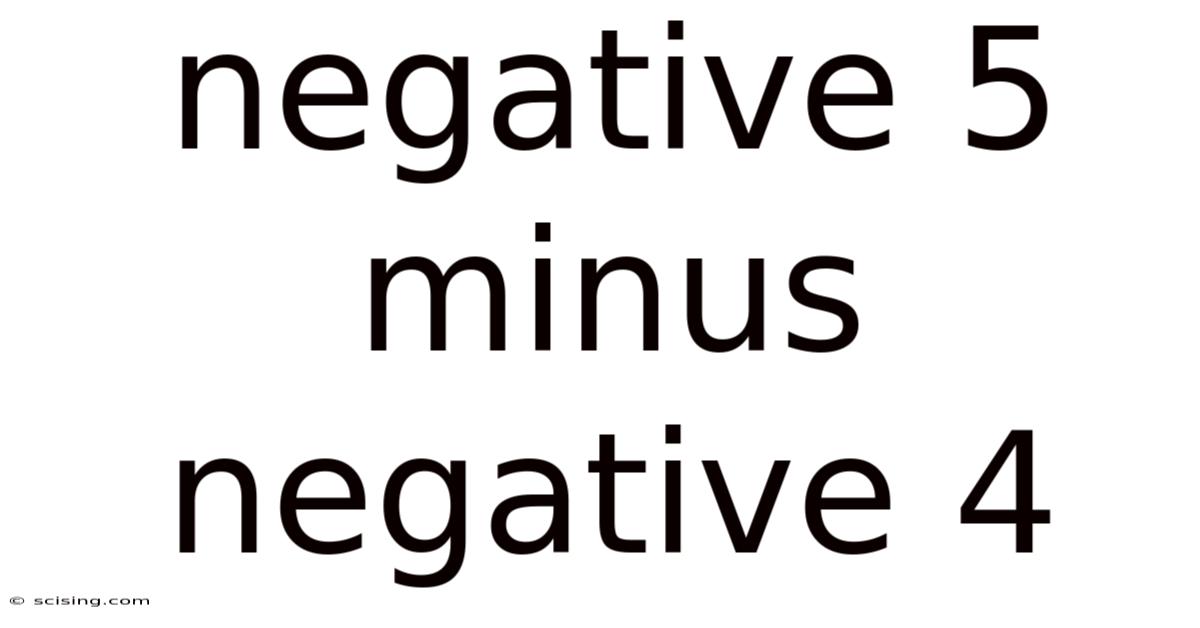
Table of Contents
Decoding -5 - (-4): A Deep Dive into Integer Subtraction
Understanding negative numbers can be tricky, especially when subtraction is involved. This article will thoroughly explore the seemingly simple calculation of -5 - (-4), explaining not only the answer but also the underlying mathematical principles. We’ll break down the concept step-by-step, addressing common misconceptions and providing a solid foundation for anyone struggling with integer arithmetic. This comprehensive guide will equip you with the knowledge to confidently tackle similar problems and build a strong grasp of number operations. By the end, you'll understand not just how to solve -5 - (-4), but why the solution works the way it does.
Understanding Negative Numbers
Before we tackle the problem, let's refresh our understanding of negative numbers. Negative numbers represent values less than zero. They are often used to represent things like debt, temperatures below freezing, or positions below a reference point. Think of a number line: zero sits in the middle, positive numbers stretch to the right, and negative numbers extend to the left.
The key to understanding operations with negative numbers is to visualize their position on this number line. This visual representation will make the abstract concepts much clearer.
The Double Negative Rule: The Heart of the Problem
The core concept that governs the solution to -5 - (-4) is the "double negative" rule. This rule states that subtracting a negative number is the same as adding its positive counterpart. In simpler terms, two minus signs next to each other cancel each other out and become a plus sign.
This might seem counterintuitive at first, but consider it this way: subtraction is the opposite of addition. If you subtract a negative number, you are essentially "taking away" a decrease. Taking away a decrease results in an increase.
Therefore, -5 - (-4) can be rewritten as -5 + 4.
Solving -5 - (-4) Step-by-Step
Now that we've established the double negative rule, let's solve the problem step-by-step:
-
Rewrite the expression: The first step is to apply the double negative rule and rewrite the expression as -5 + 4.
-
Visualize on a number line: Imagine starting at -5 on the number line. Adding 4 means moving four units to the right (towards the positive numbers).
-
Perform the addition: Starting at -5 and moving four units to the right brings us to -1.
Therefore, -5 - (-4) = -1.
A Deeper Look: The Number Line and Integer Operations
The number line provides an excellent visual aid for understanding integer operations. Let's illustrate a few examples to solidify your understanding:
-
Addition of a positive number: Adding a positive number moves you to the right on the number line. For example, -3 + 5 would move you five units to the right from -3, resulting in +2.
-
Addition of a negative number: Adding a negative number is equivalent to subtracting its positive counterpart. This means moving to the left on the number line. For example, 2 + (-3) is the same as 2 - 3, which moves you three units to the left from 2, resulting in -1.
-
Subtraction of a positive number: Subtracting a positive number moves you to the left on the number line. For instance, 5 - 3 moves you three units to the left from 5, resulting in 2.
-
Subtraction of a negative number: As we’ve already established, this is equivalent to adding the positive counterpart, moving you to the right on the number line. This reinforces the double negative rule.
Using the number line consistently will help visualize and internalize these operations.
Understanding the Concept of Opposites (Additive Inverses)
The concept of opposites, or additive inverses, is crucial to understanding negative numbers and their operations. The additive inverse of a number is the number that, when added to it, results in zero. For instance:
- The additive inverse of 5 is -5 (because 5 + (-5) = 0).
- The additive inverse of -7 is 7 (because -7 + 7 = 0).
This concept directly relates to the double negative rule. Subtracting a number is the same as adding its additive inverse.
Expanding the Concept: More Complex Problems
The principles we've discussed apply to more complex problems involving multiple negative numbers and operations. For example, let's consider the expression: -8 - (-3) + (-5) - 2.
-
Apply the double negative rule: This expression becomes -8 + 3 + (-5) - 2.
-
Rewrite addition of negative numbers as subtraction: This simplifies to -8 + 3 - 5 - 2.
-
Perform the addition and subtraction from left to right: -8 + 3 = -5. Then, -5 - 5 = -10. Finally, -10 - 2 = -12.
Therefore, -8 - (-3) + (-5) - 2 = -12.
Frequently Asked Questions (FAQ)
Q1: Why does subtracting a negative number result in addition?
A1: Subtracting a number is the opposite of adding it. Subtracting a negative number is the opposite of adding a negative number (which is moving left on the number line). The opposite of moving left is moving right, which corresponds to addition.
Q2: Can I always rewrite subtraction of a negative number as addition?
A2: Yes, this is a fundamental rule of integer arithmetic. The double negative rule always applies.
Q3: What if I have more than two negative signs together?
A3: Every pair of consecutive negative signs cancels each other out and becomes a plus sign. For example, ---5 becomes -5, and ----5 becomes +5.
Q4: Are there any real-world applications of these concepts?
A4: Yes! Negative numbers and their operations are used extensively in various fields like finance (debt), temperature measurement, and even representing changes in altitude or depth.
Conclusion
Understanding integer operations, especially subtraction involving negative numbers, is foundational to mathematical proficiency. By grasping the double negative rule and visualizing these operations on a number line, you can confidently tackle various problems involving negative numbers. This article has provided a comprehensive explanation of -5 - (-4), delving into the underlying mathematical principles and addressing common misconceptions. Remember to practice regularly and utilize the number line as a visual tool to solidify your understanding. With consistent practice and a clear understanding of the concepts, you’ll confidently navigate the world of integer arithmetic.
Latest Posts
Latest Posts
-
Characteristics Of A Traditional Economy
Sep 14, 2025
-
Genetic Flow Vs Genetic Drift
Sep 14, 2025
-
Two Bit Mathews Physical Description
Sep 14, 2025
-
4 Tons How Many Pounds
Sep 14, 2025
-
How Many Ouces In Gallon
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Negative 5 Minus Negative 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.