Negative 2 Minus Negative 5
scising
Sep 09, 2025 · 5 min read
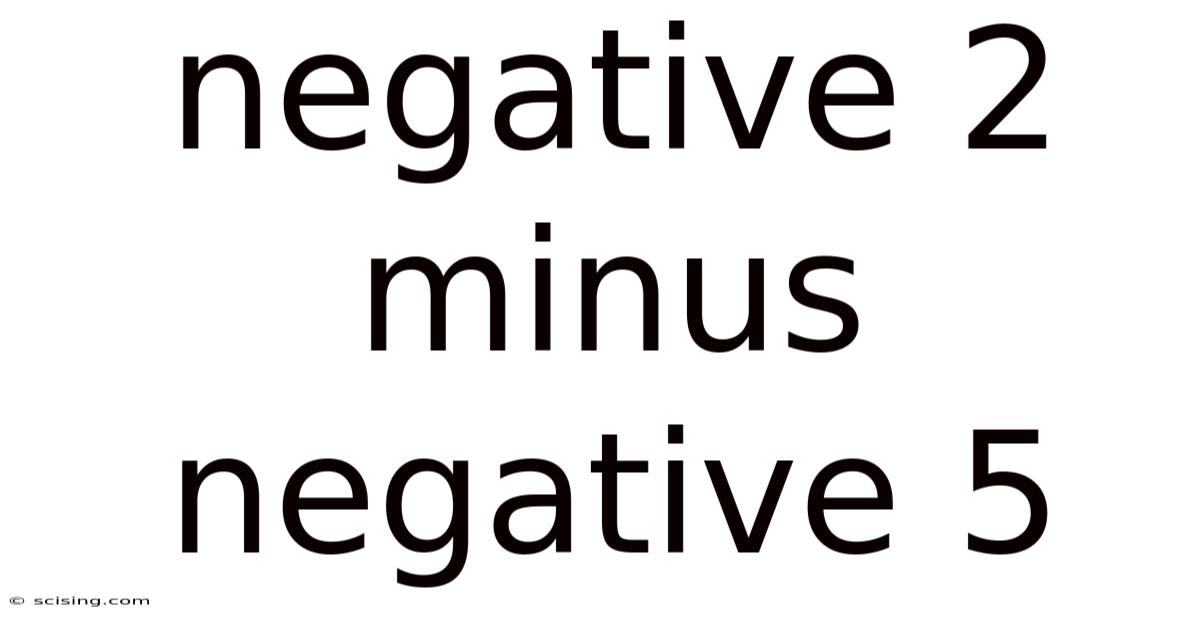
Table of Contents
Decoding the Mystery: Negative Two Minus Negative Five
Understanding the intricacies of negative numbers can be a stumbling block for many, even those comfortable with basic arithmetic. This article delves into the seemingly simple yet often confusing problem: negative two minus negative five (-2 - (-5)). We will not only solve the equation but also explore the underlying mathematical principles, providing a robust understanding of negative numbers and their operations. This explanation will be accessible to a wide range of learners, from elementary school students to those looking for a refresher on fundamental mathematical concepts. We'll also address common misconceptions and answer frequently asked questions (FAQs) to ensure a comprehensive understanding.
Introduction: Navigating the World of Negative Numbers
Negative numbers represent values less than zero. They extend the number line beyond zero in the opposite direction of positive numbers. While initially abstract, negative numbers are essential for representing real-world situations such as temperature below freezing, debt, or changes in altitude (e.g., going down a hill). Mastering operations with negative numbers, including subtraction, is crucial for various mathematical applications and problem-solving scenarios.
Understanding Subtraction as the Addition of Opposites
Before directly tackling -2 - (-5), let's establish a foundational concept: subtraction is the same as adding the opposite. This principle simplifies operations involving negative numbers significantly. The "opposite" of a number is its additive inverse – the number that, when added to the original number, results in zero. For example:
- The opposite of 5 is -5 (5 + (-5) = 0)
- The opposite of -5 is 5 (-5 + 5 = 0)
This principle is pivotal in solving our problem. The expression -2 - (-5) can be rewritten as -2 + (the opposite of -5). The opposite of -5 is 5, so the expression becomes:
-2 + 5
Solving -2 + 5: A Step-by-Step Approach
Now we have a much simpler addition problem. We can visualize this on a number line. Start at -2. Adding 5 means moving five units to the right (in the positive direction) along the number line.
- Start at -2: Imagine yourself standing at -2 on the number line.
- Add 5: Move five units to the right.
- Final Position: You will end up at 3.
Therefore, -2 + 5 = 3. Consequently, -2 - (-5) = 3.
The Mathematical Rationale: Additive Inverses and the Number Line
Let's delve deeper into the mathematical reasoning behind this result. The expression -2 - (-5) involves two negative signs. The first negative sign represents the subtraction operation. The second negative sign indicates a negative number (-5).
When we subtract a negative number, we're essentially removing a negative value. Removing a negative is equivalent to adding a positive. This is why subtracting a negative number is the same as adding its positive counterpart. This is formally expressed as the following property:
-a - (-b) = -a + b
This property is derived from the properties of additive inverses and the associative property of addition. The number line provides a visual representation of this concept. Starting at -2 and subtracting -5 means we're moving five units to the right (toward positive numbers). This reinforces the idea that subtracting a negative number has the same effect as adding a positive number.
Extending the Concept: More Complex Examples
Let's explore more complex examples to solidify our understanding:
-
-7 - (-3): This can be rewritten as -7 + 3. Starting at -7 on the number line and moving three units to the right gives us -4. Therefore, -7 - (-3) = -4.
-
-10 - (-15): This becomes -10 + 15. Starting at -10 and moving fifteen units to the right results in 5. Therefore, -10 - (-15) = 5.
-
5 - (-2): This can be rewritten as 5 + 2, which equals 7. Subtracting a negative number results in a larger positive value.
Common Mistakes and Misconceptions
A common error is treating subtracting a negative number the same as subtracting a positive number. Remembering that subtracting a negative is the same as adding a positive is crucial for avoiding errors. Another frequent mistake is incorrectly handling the order of operations. Always remember the order of operations (PEMDAS/BODMAS) to ensure accuracy in more complex calculations.
Frequently Asked Questions (FAQs)
Q1: Why does subtracting a negative number result in addition?
A1: Subtracting a number is the same as adding its opposite. The opposite of a negative number is a positive number. Therefore, subtracting a negative is equivalent to adding a positive.
Q2: Can I always rewrite subtraction as addition of the opposite?
A2: Yes, this is a fundamental principle of arithmetic. It simplifies operations involving negative numbers and makes calculations easier to visualize.
Q3: What happens if I subtract a positive number from a negative number?
A3: Subtracting a positive number from a negative number results in a more negative number. For instance, -3 - 5 = -8. You are moving further to the left on the number line.
Q4: How does this concept apply to real-world scenarios?
A4: Consider financial situations. If you owe $5 (-$5) and your debt is reduced by $2, this can be represented as -$5 - (-$2) = -$3. Your debt decreases.
Q5: Is there a visual aid to explain this concept better than a number line?
A5: While the number line is the most common and effective visual aid, you could also use counters (red for negative, blue for positive) to represent the numbers and physically manipulate them to illustrate the process of adding and subtracting.
Conclusion: Mastering Negative Number Subtraction
Understanding negative numbers and their operations is a crucial building block in mathematics. The seemingly simple problem of -2 - (-5) highlights the importance of grasping fundamental concepts such as additive inverses and rewriting subtraction as the addition of the opposite. By mastering these principles and practicing with various examples, you will build a solid foundation for tackling more complex mathematical problems. Remember that practice is key – the more you engage with these concepts, the more intuitive and effortless they will become. Don't hesitate to review this material and practice similar problems until you feel confident in your understanding. The journey towards mathematical proficiency is a rewarding one, and understanding negative numbers is a significant step on that path.
Latest Posts
Latest Posts
-
Rotational Inertia Of Point Mass
Sep 09, 2025
-
What Is A Reform Movement
Sep 09, 2025
-
Is Coffee Homogeneous Or Heterogeneous
Sep 09, 2025
-
What Is Double 3 4 Cup
Sep 09, 2025
-
What Is 70 Of 70
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about Negative 2 Minus Negative 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.