Negative 2 Minus Negative 3
scising
Sep 25, 2025 · 5 min read
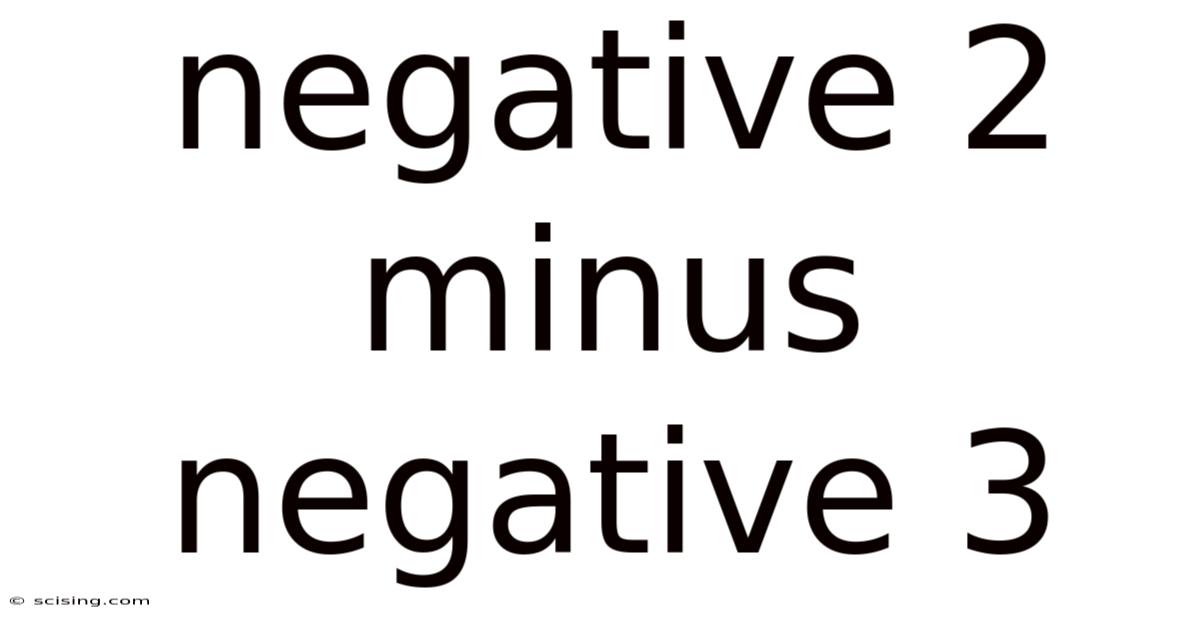
Table of Contents
Decoding the Mystery: Negative Two Minus Negative Three
Understanding the seemingly simple equation "-2 - (-3)" can be surprisingly challenging for many. This article will delve deep into the concept, explaining not just the answer but the underlying mathematical principles. We'll explore the rules of integers, the meaning of subtraction as the addition of opposites, and offer various approaches to solving this and similar problems, ultimately building a solid foundation in arithmetic. This guide is designed for anyone, from students struggling with basic math to those looking to refresh their understanding of fundamental arithmetic concepts.
Introduction: Understanding Integers and Their Operations
Before tackling "-2 - (-3)", let's establish a strong understanding of integers. Integers are whole numbers, including zero, positive numbers (like 1, 2, 3…), and their negative counterparts (-1, -2, -3…). Operations with integers – addition, subtraction, multiplication, and division – require specific rules, especially when dealing with negative numbers. Misunderstanding these rules is the most common cause of errors. This article focuses specifically on subtraction of negative integers.
The Concept of Subtraction: Adding the Opposite
Subtraction, at its core, is the inverse operation of addition. Instead of adding a number, we are taking it away. However, when dealing with negative numbers, it's often easier to visualize subtraction as adding the opposite. This is a crucial concept for solving problems involving negative integers. The opposite of a number is simply its additive inverse. For example:
- The opposite of 5 is -5.
- The opposite of -5 is 5.
Therefore, "-2 - (-3)" can be rewritten as "-2 + 3". This transformation is the key to simplifying the problem significantly. By changing the subtraction of a negative number to the addition of its positive counterpart, we move from the complexities of subtracting negatives to the more familiar territory of adding integers.
Step-by-Step Solution: Visualizing the Problem
Now, let's solve "-2 - (-3)" step-by-step, using the principle of adding the opposite:
-
Rewrite the equation: "-2 - (-3)" becomes "-2 + 3". This is the crucial first step. We are essentially converting the subtraction of a negative into the addition of a positive.
-
Visual Representation (Number Line): Imagine a number line. Start at -2. Adding 3 means moving three units to the right along the number line.
-
Performing the Addition: Starting at -2, move three units to the right. You will land on 1.
-
Final Answer: Therefore, -2 - (-3) = 1.
Alternative Approaches and Deeper Understanding
While the method of "adding the opposite" is often the most straightforward, other methods can help solidify understanding:
-
Using Absolute Values: The absolute value of a number is its distance from zero, always expressed as a positive number. For example, | -2 | = 2 and | 3 | = 3. While not directly applicable to the entire subtraction process, understanding absolute value helps build intuition about the magnitude of numbers.
-
Chip Model (or Counters): This is a visual method helpful for beginners. Represent -2 with two red chips (representing negative values) and +3 with three blue chips (representing positive values). When you combine them, two red and two blue cancel each other out (resulting in zero), leaving one blue chip. This visually demonstrates the final answer of 1.
-
Debt and Credit Analogy: Think of -2 as a debt of 2 units. Subtracting a debt (-3) is like having that debt removed. So, removing a debt of 3 units from a debt of 2 units leaves you with a credit of 1 unit (positive 1).
Expanding the Concept: More Complex Problems
The principle of "adding the opposite" applies to more complex problems involving multiple negative numbers. Consider this example:
-5 - (-2) - (-4)
-
Rewrite using addition of opposites: -5 + 2 + 4
-
Solve from left to right (or regroup): (-5 + 2) + 4 = -3 + 4 = 1
Alternatively, you could regroup: -5 + (2 + 4) = -5 + 6 = 1
The answer remains the same, highlighting the commutative property of addition (the order doesn't change the result).
The Importance of Parentheses
Parentheses are crucial in mathematical expressions. They dictate the order of operations. In "-2 - (-3)", the parentheses around "-3" are essential. They signify that the negative sign belongs to the 3, making it a negative integer. Without the parentheses, "-2 - -3" would be ambiguous and likely interpreted differently.
Frequently Asked Questions (FAQ)
-
Q: What if I have more than two negative numbers being subtracted? A: The same principle applies. Rewrite each subtraction of a negative as an addition of a positive. Then, solve using the rules of integer addition.
-
Q: Why can't I just subtract the numbers directly? A: While you can in simple cases, it's easy to make mistakes when dealing with multiple negatives or a mix of positive and negative numbers. The "adding the opposite" method provides a consistent and reliable approach.
-
Q: Are there other ways to visualize this? A: Yes! Many visual aids and manipulatives can help understand integer operations. Explore different methods to find what resonates best with your learning style.
-
Q: What happens if the result is negative? A: If the final result after adding the opposite is negative, it simply means the result is a negative integer. For example, -5 - 2 = -7.
-
Q: How does this relate to algebra? A: The principles of integer operations are fundamental to algebra. Understanding how to manipulate negative numbers is critical for solving algebraic equations and inequalities.
Conclusion: Mastering Negative Number Subtraction
Understanding negative number subtraction, particularly problems like "-2 - (-3)", is a cornerstone of mathematical proficiency. The key lies in transforming the problem into the addition of opposites. By consistently applying this technique and exploring different visual aids, you can build a confident and accurate approach to solving problems involving negative integers. This understanding will serve as a solid foundation for more advanced mathematical concepts. Remember, practice is crucial. The more you work with these problems, the more intuitive and effortless they will become. Don't hesitate to explore different methods and find the one that clicks for you. Mastering this seemingly simple concept opens the door to a wider understanding of the world of mathematics.
Latest Posts
Latest Posts
-
How Long Is 35 Months
Sep 25, 2025
-
Title Page Of A Book
Sep 25, 2025
-
Mosaic Covenant In The Bible
Sep 25, 2025
-
Examples For Subject And Predicate
Sep 25, 2025
-
35 Percent Off Of 40
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about Negative 2 Minus Negative 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.