Negative 1 Minus Negative 4
scising
Sep 24, 2025 · 6 min read
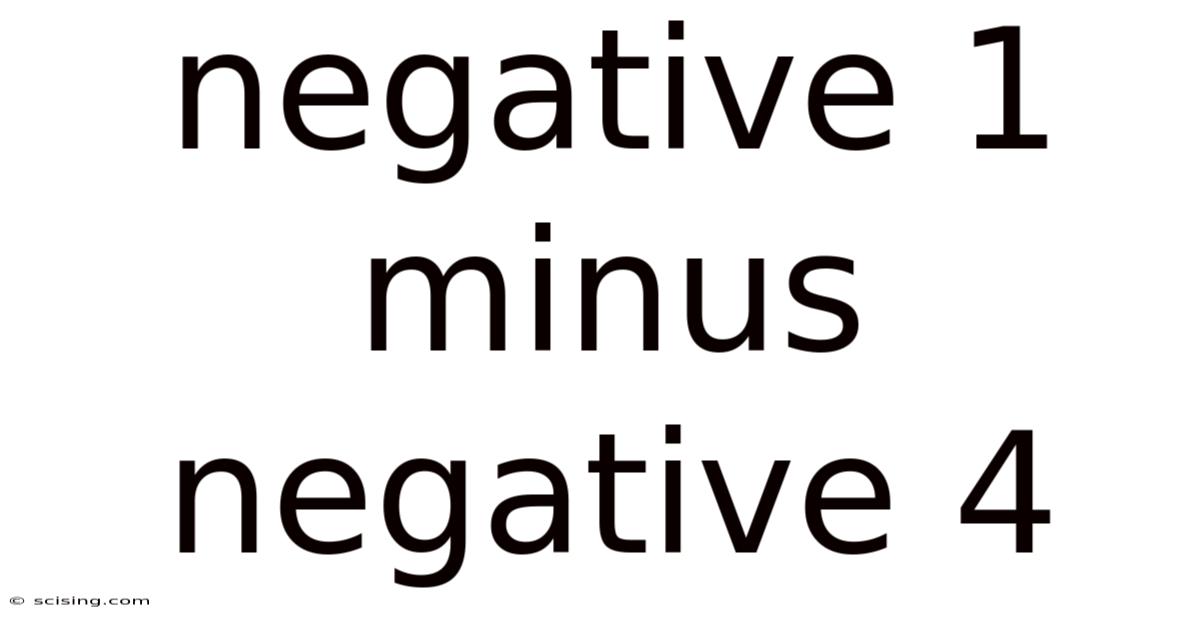
Table of Contents
Unraveling the Mystery: Negative One Minus Negative Four
Understanding negative numbers can be tricky, but mastering them is crucial for success in mathematics and beyond. This article will delve deep into the seemingly simple problem of "-1 - (-4)," explaining not only the solution but also the underlying principles of integer operations, offering various approaches to solving similar problems, and addressing common misconceptions. We'll explore the concept of negative numbers, subtraction as adding the opposite, and the visual representation of these operations on a number line. By the end, you'll not only know the answer but also possess a solid understanding of the mechanics behind it.
Introduction: Navigating the World of Negative Numbers
Negative numbers represent values less than zero. They are commonly used to represent things like debt, temperatures below freezing, or positions below sea level. While initially challenging, understanding negative numbers unlocks a significant portion of mathematical concepts. This article focuses on solving "-1 - (-4)," a problem that perfectly exemplifies the complexities and nuances of operations involving negative integers. We’ll break down the process step-by-step, ensuring clarity and comprehension for all readers, regardless of their prior mathematical experience.
Understanding Subtraction: The Concept of "Adding the Opposite"
Subtraction, at its core, is the inverse operation of addition. While we often visualize subtraction as taking away, a powerful way to understand subtraction with negative numbers is by framing it as adding the opposite. This principle significantly simplifies calculations involving negative integers.
To add the opposite, follow these steps:
- Identify the subtraction: Locate the subtraction sign in the equation.
- Change the sign of the second number: Change the sign of the number immediately following the subtraction sign. If it's positive, make it negative; if it's negative, make it positive.
- Change the subtraction to addition: Replace the subtraction sign with an addition sign.
Let's apply this to our problem: "-1 - (-4)".
- Subtraction identified: The subtraction sign is between -1 and (-4).
- Change the sign: The second number, -4, becomes +4.
- Change to addition: The expression becomes "-1 + 4".
Now, we have a much simpler addition problem to solve.
Solving -1 + 4: Different Approaches
We can solve "-1 + 4" using several approaches:
-
Number Line Visualization: Start at -1 on the number line. Adding 4 means moving four units to the right (in the positive direction). This will land you at +3.
-
Integer Chips: Imagine using integer chips, where red chips represent negative numbers and blue chips represent positive numbers. We start with one red chip (-1). Adding four positive chips (+4) means we now have four blue chips and one red chip. A red chip and a blue chip cancel each other out (resulting in zero), leaving us with three blue chips, representing +3.
-
Abstract Calculation: We can think of this as finding the difference between 4 and 1. Since 4 is larger and positive, the result will be positive. The difference between 4 and 1 is 3, therefore -1 + 4 = 3.
Therefore, -1 - (-4) = 3.
The Significance of Parentheses
Parentheses play a crucial role in mathematical expressions, particularly those involving negative numbers. They indicate the order of operations and group terms. In our original problem, the parentheses around -4 are essential. They signify that the entire -4 is being subtracted, not just the 4. Without the parentheses, the expression "-1 - -4" would be ambiguous and potentially lead to incorrect interpretations.
Expanding on the Concept: More Examples
Let's explore more examples to solidify our understanding:
-
-5 - (-2): Following the "add the opposite" rule, this becomes -5 + 2. Visualizing this on a number line, or using integer chips, results in -3.
-
3 - (-7): This translates to 3 + 7, which equals 10.
-
-2 - 5: This is equivalent to -2 + (-5), resulting in -7. Note that this is different from adding the opposite rule; we apply it only to subtraction of a negative number.
-
-8 - (-8): This becomes -8 + 8, which equals 0.
These examples demonstrate the consistent application of the "add the opposite" rule. This rule simplifies the process and eliminates confusion associated with subtracting negative numbers.
Addressing Common Misconceptions
Many students struggle with negative numbers. Here are some common misconceptions to be aware of:
-
Double Negative Confusion: Students sometimes mistakenly think that two negative signs cancel out to become a positive sign only under certain circumstances. This is not true in all cases. It's only true when they occur consecutively as in subtraction of negative numbers.
-
Ignoring Parentheses: Forgetting the significance of parentheses leads to incorrect interpretations and incorrect solutions. Always pay close attention to the placement and meaning of parentheses.
-
Misinterpreting Subtraction: Thinking of subtraction purely as "taking away" can lead to difficulty when dealing with negative numbers. Understanding subtraction as "adding the opposite" provides a more robust and universal approach.
Further Applications and Real-World Examples
Understanding operations with negative numbers extends far beyond simple arithmetic. They are fundamental to:
-
Algebra: Solving equations and inequalities often involves manipulating negative numbers.
-
Calculus: Derivatives and integrals frequently incorporate negative numbers.
-
Physics: Negative numbers represent quantities like negative velocity (opposite direction) or negative acceleration (deceleration).
-
Finance: Negative numbers represent debts or losses.
-
Temperature: Temperatures below zero are represented using negative numbers.
Frequently Asked Questions (FAQ)
Q: Why is subtracting a negative number the same as adding a positive number?
A: Subtraction is the inverse of addition. Subtracting a negative number is like "undoing" the subtraction of a positive number. It's analogous to having a debt (negative) and then removing that debt (subtracting the negative), which results in an increase in your assets (adding a positive).
Q: Can I solve these problems without using the "add the opposite" rule?
A: Yes, you can visualize the problem using a number line or integer chips. However, the "add the opposite" rule provides a more efficient and systematic approach, especially for more complex problems.
Q: What if I have more than two negative numbers in the equation?
A: Apply the "add the opposite" rule to each instance of subtraction of a negative number. Then simplify the resulting expression following the order of operations (PEMDAS/BODMAS).
Q: Are there other ways to represent negative numbers?
A: Yes, negative numbers can be represented on a number line, with integer chips, or using different notations depending on the context (e.g., in computer science, they might be represented using two's complement).
Conclusion: Mastering Negative Numbers
Understanding operations with negative numbers is a cornerstone of mathematical fluency. This article explored the problem "-1 - (-4)" in depth, demonstrating that the answer is 3. By mastering the "add the opposite" rule and visualizing the operations, you can confidently tackle more complex problems involving negative integers. Remember to pay attention to parentheses and avoid common misconceptions. With consistent practice and a clear understanding of the underlying concepts, you’ll overcome any challenges posed by negative numbers and build a strong foundation in mathematics. The key is to approach these problems systematically and to consistently apply the principles discussed above.
Latest Posts
Latest Posts
-
Acid And Base Experiments Idea
Sep 25, 2025
-
How Much Is 96 Oz
Sep 25, 2025
-
Hugs And Kisses In Spanish
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about Negative 1 Minus Negative 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.