Negative 1 Minus Negative 1
scising
Sep 22, 2025 · 5 min read
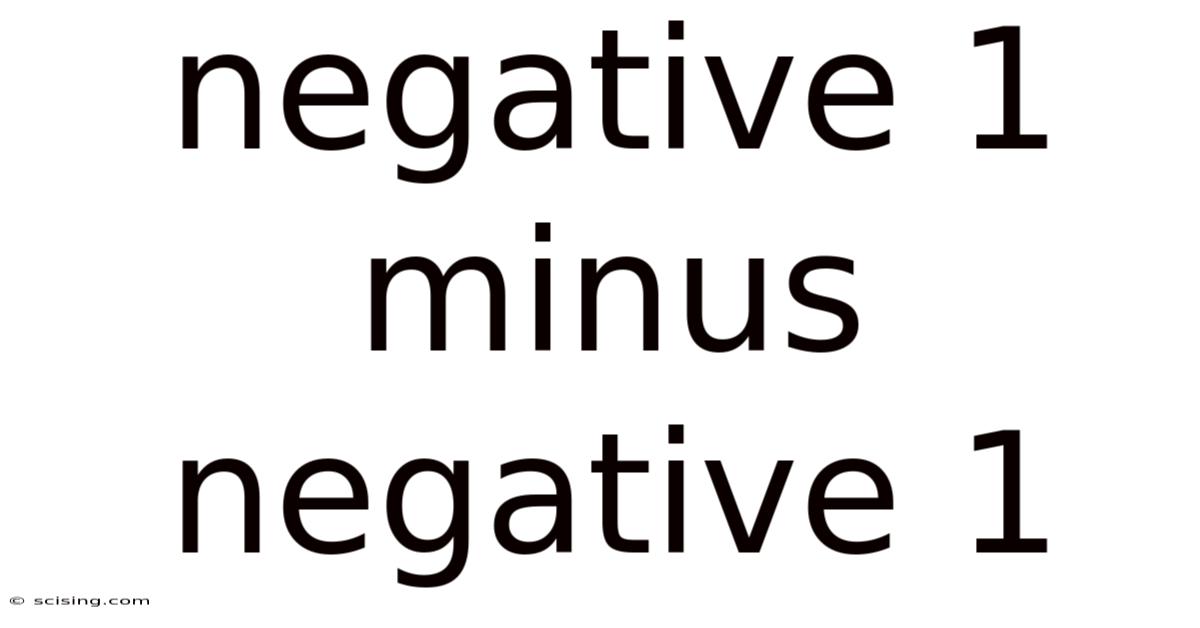
Table of Contents
Decoding -1 - (-1): A Deep Dive into Integer Subtraction
Understanding the seemingly simple equation "-1 - (-1)" requires a solid grasp of integer arithmetic, specifically subtraction involving negative numbers. This seemingly basic calculation holds the key to understanding more complex mathematical concepts. This article will break down this equation step-by-step, explore the underlying principles, and delve into the broader context of integer operations, making it accessible to anyone regardless of their prior mathematical background.
Introduction: Understanding Negative Numbers
Before tackling the equation, let's establish a strong foundation. Negative numbers represent values less than zero. They are often used to represent quantities like debt, temperature below zero, or positions below a reference point. Understanding their behavior in mathematical operations is crucial. Think of a number line: positive numbers extend to the right of zero, while negative numbers extend to the left.
Visualizing Subtraction: The Number Line Approach
A number line provides a powerful visual tool for understanding subtraction. Subtraction can be visualized as movement to the left on the number line. For instance, 5 - 2 means starting at 5 and moving two units to the left, landing on 3.
Now, let's apply this to negative numbers. The equation -1 - (-1) can be visualized as follows:
- Start at -1: Place your finger on -1 on the number line.
- Subtract -1: Subtracting a negative number is equivalent to adding its positive counterpart. So, subtracting -1 means moving one unit to the right on the number line.
This movement from -1, one unit to the right, lands us precisely at 0. Therefore, -1 - (-1) = 0.
The Mathematical Explanation: Subtracting Negative Numbers
The core principle underpinning the solution lies in the concept of subtracting a negative number. Subtracting a negative number is the same as adding its positive counterpart. This is because subtraction is the inverse operation of addition.
Let's break it down mathematically:
-
Subtraction as adding the opposite: Subtraction can be redefined as adding the additive inverse (opposite) of the second number. The additive inverse of a number is the number that, when added to the original number, results in zero. For example, the additive inverse of 5 is -5, and the additive inverse of -5 is 5.
-
Applying this to -1 - (-1): The equation can be rewritten as: -1 + (+1). We've replaced subtracting -1 with adding its additive inverse, which is +1.
-
Simplifying the equation: -1 + 1 = 0. This confirms our visual understanding from the number line.
Extending the Concept: More Complex Examples
Let's apply this understanding to more complex examples to solidify our understanding.
-
-5 - (-3): This can be rewritten as -5 + 3 = -2. We start at -5 on the number line and move 3 units to the right.
-
-2 - (-7): This becomes -2 + 7 = 5. We begin at -2 and move 7 units to the right.
-
3 - (-4): This is equivalent to 3 + 4 = 7. Starting at 3, we move 4 units to the right.
These examples illustrate the consistent pattern: subtracting a negative number always results in addition. This is a fundamental rule in integer arithmetic and is crucial for solving more complex algebraic equations.
The Role of the Number Line in Mathematical Understanding
The number line is not just a visual aid; it's a fundamental tool for grasping the concepts of integers and their operations. It helps to build an intuitive understanding of how numbers relate to each other, especially when dealing with negative values. The number line provides a concrete representation that complements abstract mathematical rules.
Visualizing mathematical operations on the number line enhances understanding and problem-solving skills. It helps to bridge the gap between abstract concepts and concrete representation, especially helpful for learners who benefit from visual learning styles.
The Importance of Understanding Additive Inverses
The concept of additive inverses is pivotal in various areas of mathematics. It's not limited to integer arithmetic; it extends to rational numbers, real numbers, and even more complex number systems. Understanding additive inverses allows for simplification of equations and a deeper understanding of how numbers interact. It's a foundational concept for solving equations, particularly those involving negative numbers.
Frequently Asked Questions (FAQs)
Q1: Why is subtracting a negative the same as adding a positive?
A1: Subtraction is the inverse operation of addition. Subtracting a number is essentially asking "What do I need to add to get back to zero?". If you start with a negative number and want to "undo" it (get to zero), you need to add its positive counterpart.
Q2: Can I always rewrite subtraction as addition?
A2: Yes, you can always rewrite subtraction as adding the additive inverse. This applies to all numbers, not just integers. This is a powerful technique for simplifying equations and solving problems.
Q3: What happens if I subtract a positive number from a negative number?
A3: If you subtract a positive number from a negative number, you move further to the left on the number line, resulting in a more negative number. For example, -3 - 2 = -5.
Q4: Is there a difference between -1 - (-1) and (-1) - (-1)?
A4: No, there is no difference. Parentheses are used for grouping terms, but in this specific case, they don't alter the order of operations. Both expressions simplify to 0.
Conclusion: Mastering Integer Arithmetic
Understanding "-1 - (-1) = 0" is not just about getting the right answer; it's about grasping the fundamental principles of integer subtraction and additive inverses. This knowledge forms a cornerstone for more advanced mathematical concepts. By mastering these fundamental principles, students can confidently tackle more complex problems in algebra, calculus, and other areas of mathematics. Remember the visualization on the number line, the concept of additive inverses, and the rule of transforming subtraction into addition. This holistic approach makes learning mathematics more intuitive and enjoyable. The seemingly simple equation -1 - (-1) unlocks a deeper understanding of the elegance and logic of mathematics. Through consistent practice and application, you can build a strong foundation in integer arithmetic and move towards more advanced mathematical concepts with confidence.
Latest Posts
Latest Posts
-
First Chapter Of Animal Farm
Sep 23, 2025
-
I Sent It In Spanish
Sep 23, 2025
-
Lewis Dot Structure For Asf3
Sep 23, 2025
-
Is Water Solute Or Solvent
Sep 23, 2025
-
Rock Of Ages Hymn Meaning
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Negative 1 Minus Negative 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.