Lcm Of 12 And 8
scising
Sep 06, 2025 · 6 min read
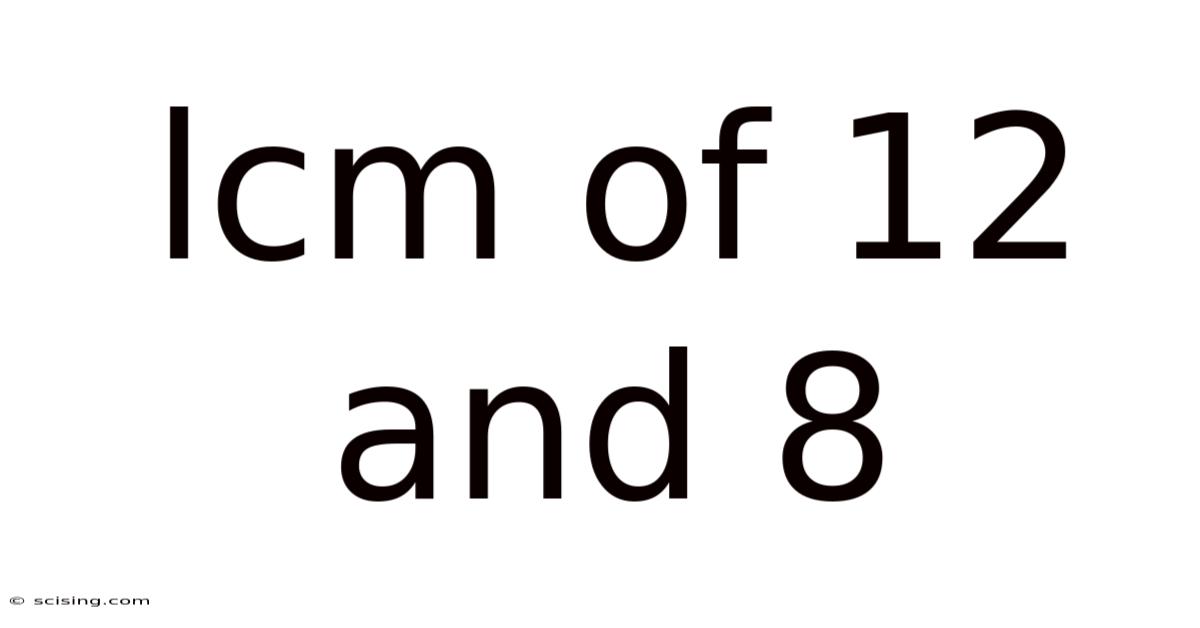
Table of Contents
Finding the Least Common Multiple (LCM) of 12 and 8: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the concept thoroughly unlocks a deeper appreciation for number theory and its applications in various fields. This comprehensive guide delves into the LCM of 12 and 8, exploring multiple methods to calculate it, explaining the underlying mathematical principles, and showcasing its relevance in real-world scenarios. Whether you're a student grappling with number theory or simply curious about the intricacies of mathematics, this article will provide a clear and insightful understanding of the LCM.
Introduction: What is the Least Common Multiple (LCM)?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the given integers. In simpler terms, it's the smallest number that contains all the given numbers as factors. Understanding LCM is crucial in various mathematical operations, particularly when dealing with fractions, simplifying expressions, and solving problems involving ratios and proportions. This article focuses specifically on determining the LCM of 12 and 8, using several different methods to illustrate the concept thoroughly.
Method 1: Listing Multiples
This is a straightforward method, particularly effective for smaller numbers. We list the multiples of each number until we find the smallest multiple that is common to both.
- Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, ...
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, 104, 112, 120, ...
By comparing the lists, we see that the smallest common multiple is 24. Therefore, the LCM of 12 and 8 is 24. This method is intuitive but can become cumbersome for larger numbers.
Method 2: Prime Factorization
This method utilizes the fundamental theorem of arithmetic, which states that every integer greater than 1 can be represented uniquely as a product of prime numbers. This approach is more efficient for larger numbers.
-
Find the prime factorization of each number:
- 12 = 2 x 2 x 3 = 2² x 3
- 8 = 2 x 2 x 2 = 2³
-
Identify the highest power of each prime factor present in the factorizations:
- The prime factors are 2 and 3.
- The highest power of 2 is 2³ = 8.
- The highest power of 3 is 3¹ = 3.
-
Multiply the highest powers of all prime factors:
- LCM(12, 8) = 2³ x 3 = 8 x 3 = 24
This method provides a systematic and efficient way to calculate the LCM, regardless of the size of the numbers involved.
Method 3: Greatest Common Divisor (GCD) Method
The LCM and the greatest common divisor (GCD) of two numbers are related through a simple formula:
LCM(a, b) = (|a x b|) / GCD(a, b)
where |a x b| represents the absolute value of the product of a and b.
-
Find the GCD of 12 and 8 using the Euclidean algorithm:
- Divide the larger number (12) by the smaller number (8): 12 = 1 x 8 + 4
- Replace the larger number with the smaller number (8) and the smaller number with the remainder (4): 8 = 2 x 4 + 0
- The GCD is the last non-zero remainder, which is 4. Therefore, GCD(12, 8) = 4.
-
Apply the formula:
- LCM(12, 8) = (12 x 8) / 4 = 96 / 4 = 24
This method is particularly useful when dealing with larger numbers, as finding the GCD is often easier than directly finding the LCM using other methods. The Euclidean algorithm provides an efficient way to calculate the GCD.
Method 4: Venn Diagram Method (for Visual Learners)
This method uses a Venn diagram to visualize the prime factorization and determine the LCM.
-
Prime Factorize each number: As before, 12 = 2² x 3 and 8 = 2³.
-
Represent the prime factors in a Venn diagram: Draw two overlapping circles, one for the prime factors of 12 and one for the prime factors of 8.
-
Place the common factors in the overlapping region: Both 12 and 8 share two factors of 2. Place these two '2's in the overlapping region.
-
Place the remaining factors in their respective circles: 12 has one remaining factor of 3, and 8 has one remaining factor of 2.
-
Multiply all the factors in the diagram: To find the LCM, multiply all the factors present in the Venn diagram: 2 x 2 x 2 x 3 = 24.
Understanding the Mathematical Principles
The LCM is fundamentally linked to the concept of divisibility. A number 'a' is divisible by another number 'b' if the remainder of the division of 'a' by 'b' is zero. The LCM is the smallest number that satisfies the divisibility condition for all the given numbers. The prime factorization method highlights the essential role of prime numbers in building up composite numbers and determining their multiples. The relationship between the LCM and GCD showcases a fundamental duality in number theory.
Real-World Applications of LCM
The concept of LCM finds numerous applications in various fields:
-
Scheduling: Imagine two buses arrive at a bus stop at different intervals. The LCM of their intervals helps determine when they will arrive at the stop simultaneously.
-
Fraction operations: When adding or subtracting fractions with different denominators, finding the LCM of the denominators is essential to find a common denominator for simplification.
-
Gear ratios: In mechanical engineering, the LCM is used to calculate gear ratios and synchronized rotations in complex machinery.
-
Cyclic events: In situations involving cyclical events, such as planetary alignments or repeating patterns, the LCM helps determine when these events coincide.
Frequently Asked Questions (FAQ)
-
What is the difference between LCM and GCD? The least common multiple (LCM) is the smallest multiple common to both numbers, while the greatest common divisor (GCD) is the largest factor common to both numbers.
-
Can the LCM of two numbers be smaller than one of the numbers? No. The LCM of two numbers will always be greater than or equal to the larger of the two numbers.
-
How do I find the LCM of more than two numbers? You can extend the prime factorization or GCD methods to find the LCM of more than two numbers. For the prime factorization method, consider the highest power of each prime factor present in the factorization of all the numbers.
Conclusion
Determining the LCM of 12 and 8, as demonstrated through various methods, serves as a foundational exercise in understanding fundamental number theory concepts. The ability to calculate the LCM efficiently is crucial for various mathematical operations and real-world applications. Understanding the different methods—listing multiples, prime factorization, GCD method, and the Venn diagram approach—provides a comprehensive grasp of the LCM's calculation and its underlying principles. This knowledge is not merely an academic exercise but a practical tool with far-reaching implications in diverse fields. Mastering the LCM opens doors to deeper explorations in mathematics and enhances problem-solving skills across various disciplines.
Latest Posts
Latest Posts
-
Bee Marabou Stork Symbiotic Relationship
Sep 06, 2025
-
Last Names Starting With Mc
Sep 06, 2025
-
When Did New Testament Start
Sep 06, 2025
-
How Big Do Minnows Get
Sep 06, 2025
-
William Golding Passion And Talent
Sep 06, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 12 And 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.