Is 5/6 Greater Than 2/3
scising
Sep 21, 2025 · 5 min read
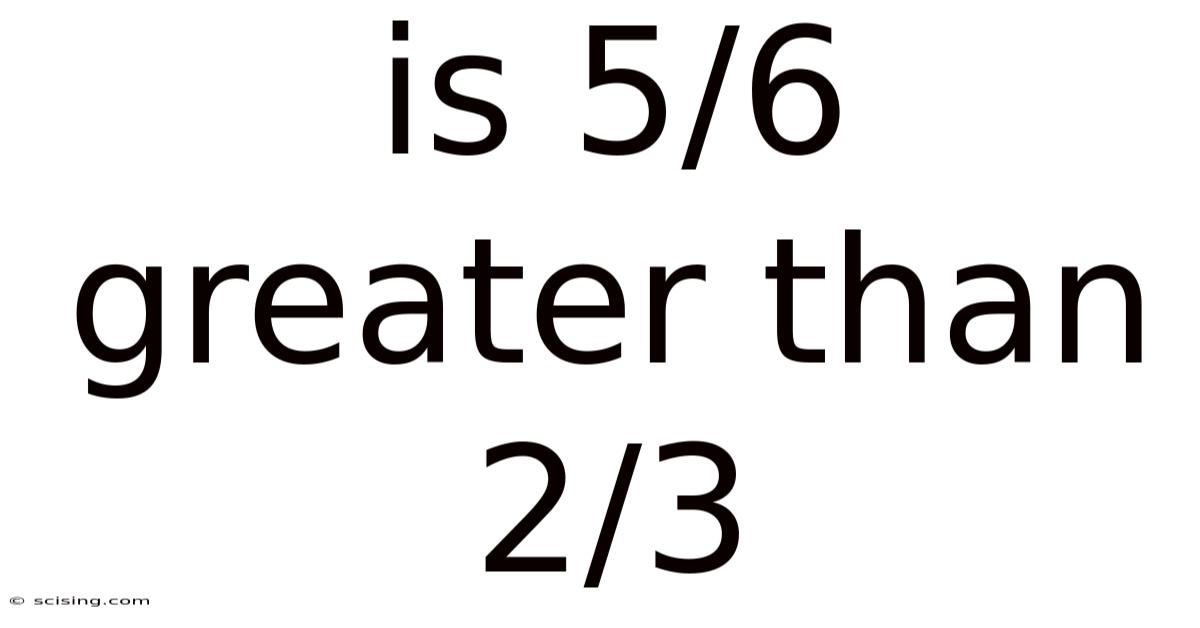
Table of Contents
Is 5/6 Greater Than 2/3? A Comprehensive Exploration of Fraction Comparison
Understanding fractions is a fundamental skill in mathematics, crucial for everything from baking a cake to calculating complex engineering problems. This article will delve into the question: Is 5/6 greater than 2/3? We'll not only answer this specific question definitively but also explore the underlying concepts and various methods for comparing fractions, equipping you with the tools to confidently tackle similar comparisons in the future. This guide will cover various approaches, from visual representations to numerical calculations, ensuring a thorough understanding for learners of all levels.
Introduction: Understanding Fractions
Before we dive into comparing 5/6 and 2/3, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a numerator (the top number) over a denominator (the bottom number), separated by a line. The numerator indicates how many parts we have, and the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 2/3, the numerator is 2, and the denominator is 3. This means we have 2 parts out of a total of 3 equal parts.
Method 1: Visual Comparison using Fraction Bars
A simple and intuitive way to compare fractions is by using visual aids like fraction bars. Imagine two identical bars representing the whole. Divide the first bar into six equal parts and shade five of them to represent 5/6. Divide the second bar into three equal parts and shade two of them to represent 2/3. By visually comparing the shaded portions, it becomes clear that the shaded area representing 5/6 is larger than the shaded area representing 2/3. This visual demonstration immediately shows that 5/6 > 2/3.
Method 2: Finding a Common Denominator
A more robust method for comparing fractions involves finding a common denominator. This is a number that is a multiple of both denominators. For 5/6 and 2/3, the least common denominator (LCD) is 6. We can rewrite 2/3 with a denominator of 6 by multiplying both the numerator and the denominator by 2:
(2/3) * (2/2) = 4/6
Now we can easily compare 5/6 and 4/6. Since 5 > 4, we can conclude that 5/6 > 2/3. This method is particularly useful when visual comparison isn't practical or when dealing with more complex fractions.
Method 3: Converting Fractions to Decimals
Another approach is to convert the fractions to decimals. We can do this by dividing the numerator by the denominator:
5/6 ≈ 0.833
2/3 ≈ 0.667
Comparing the decimal values, we see that 0.833 > 0.667, confirming that 5/6 > 2/3. This method provides a numerical comparison that's easy to understand and is especially helpful when dealing with fractions that don't have easily identifiable common denominators.
Method 4: Cross-Multiplication
A more advanced, yet efficient method for comparing fractions involves cross-multiplication. We multiply the numerator of the first fraction by the denominator of the second fraction, and vice-versa. Then we compare the products:
5/6 ? 2/3
5 * 3 = 15
6 * 2 = 12
Since 15 > 12, we conclude that 5/6 > 2/3. This method works because it implicitly finds a common denominator and compares the resulting numerators.
A Deeper Dive into Fraction Comparison: The Concept of Equivalence
It's important to understand that fractions can represent the same value even if they look different. For example, 1/2 is equivalent to 2/4, 3/6, and countless other fractions. This equivalence stems from the fact that multiplying or dividing both the numerator and the denominator by the same non-zero number doesn't change the value of the fraction. This principle is crucial when finding common denominators for fraction comparisons.
Practical Applications: Why Comparing Fractions Matters
The ability to compare fractions is essential in many real-world scenarios:
- Baking and Cooking: Following recipes often requires understanding fractional measurements. Knowing whether 1/2 cup is more or less than 2/3 cup is crucial for achieving the desired outcome.
- Construction and Engineering: Precise measurements are paramount in these fields. Comparing fractions is essential for ensuring accuracy in building structures, designing machinery, and more.
- Finance and Budgeting: Managing personal finances often involves dealing with fractions of amounts (e.g., portions of a budget).
- Data Analysis: Many statistical calculations and data representations involve fractions and the need to compare their magnitudes.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to compare fractions? A: Yes, you can convert fractions to decimals using a calculator and then compare the resulting decimal values. However, understanding the underlying mathematical principles is crucial for broader comprehension.
-
Q: What if the fractions have different signs (positive and negative)? A: When comparing fractions with different signs, the positive fraction is always greater than the negative fraction. For example, 1/2 > -2/3.
-
Q: Are there other methods for comparing fractions besides the ones mentioned? A: Yes, there are more advanced techniques, such as converting fractions to percentages or using number lines, but the methods described above are sufficient for most common scenarios.
-
Q: What is the importance of understanding the least common denominator (LCD)? A: Finding the LCD simplifies the process of comparing fractions, as it allows for a direct comparison of numerators. Using a larger common denominator is possible but less efficient.
Conclusion: Mastering Fraction Comparison
Comparing fractions is a fundamental mathematical skill with widespread applications. We've explored several methods – visual comparison, finding a common denominator, converting to decimals, and cross-multiplication – to determine whether 5/6 is greater than 2/3. The answer is a resounding yes, as demonstrated through each of these methods. By mastering these techniques, you'll develop a solid foundation in fraction arithmetic and confidently tackle various mathematical challenges involving fractions in your academic pursuits and everyday life. Remember that understanding the underlying principles is just as crucial as mastering the mechanics of calculation. The more you practice, the more intuitive and effortless fraction comparison will become.
Latest Posts
Latest Posts
-
Difference Between Tundra And Taiga
Sep 21, 2025
-
What Is A Replication Bubble
Sep 21, 2025
-
Characteristics Of Traditional Economic System
Sep 21, 2025
-
Economy For New England Colonies
Sep 21, 2025
-
Squealer Quotes From Animal Farm
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Is 5/6 Greater Than 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.