Is 3/4 Greater Than 2/3
scising
Sep 24, 2025 · 5 min read
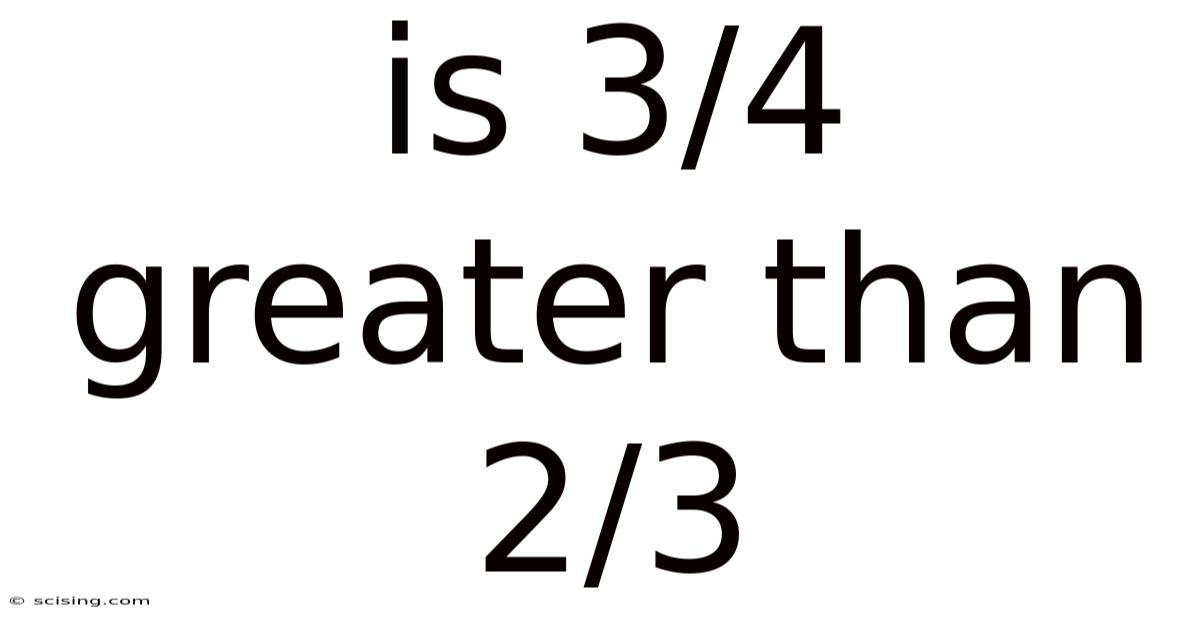
Table of Contents
Is 3/4 Greater Than 2/3? A Deep Dive into Fraction Comparison
Is 3/4 greater than 2/3? This seemingly simple question about fractions opens the door to a deeper understanding of fundamental mathematical concepts. While the answer itself might be quickly apparent to some, exploring the why behind the answer provides a valuable learning opportunity, strengthening foundational math skills crucial for more advanced studies. This article will not only answer the question definitively but also explore various methods for comparing fractions, providing you with a comprehensive understanding of the topic. We'll delve into the practical applications of fraction comparison and address common misconceptions.
Understanding Fractions: A Quick Refresher
Before diving into the comparison, let's briefly revisit the concept of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator shows how many of those parts are being considered.
For example, in the fraction 3/4, the denominator 4 signifies that the whole is divided into four equal parts. The numerator 3 indicates that we are considering three of those four parts.
Method 1: Finding a Common Denominator
The most straightforward method for comparing fractions is to find a common denominator. This involves converting both fractions so they share the same denominator. Once they have the same denominator, we can directly compare their numerators.
Let's apply this method to compare 3/4 and 2/3:
-
Find the Least Common Multiple (LCM): We need to find the smallest number that is a multiple of both 4 and 3. The multiples of 4 are 4, 8, 12, 16... and the multiples of 3 are 3, 6, 9, 12, 15... The least common multiple of 4 and 3 is 12.
-
Convert the Fractions: We'll convert both fractions to have a denominator of 12:
-
For 3/4: To get a denominator of 12, we multiply both the numerator and the denominator by 3 (because 4 x 3 = 12): (3 x 3) / (4 x 3) = 9/12
-
For 2/3: To get a denominator of 12, we multiply both the numerator and the denominator by 4 (because 3 x 4 = 12): (2 x 4) / (3 x 4) = 8/12
-
-
Compare the Numerators: Now that both fractions have the same denominator, we can compare their numerators. Since 9 > 8, we can conclude that 9/12 > 8/12.
-
Conclusion: Therefore, 3/4 > 2/3.
Method 2: Converting to Decimals
Another effective method is to convert both fractions into decimals. This involves dividing the numerator by the denominator for each fraction.
- 3/4 = 0.75
- 2/3 = 0.666... (a repeating decimal)
By comparing the decimal values, it's clear that 0.75 > 0.666..., confirming that 3/4 > 2/3. This method is particularly useful when dealing with fractions that are difficult to convert to a common denominator.
Method 3: Visual Representation
A visual approach can be highly effective, particularly for those who prefer a more intuitive understanding. Imagine two identical pies.
- Divide one pie into four equal slices and shade three of them (representing 3/4).
- Divide the other pie into three equal slices and shade two of them (representing 2/3).
By visually comparing the shaded portions, it becomes evident that the three-quarters slice of the first pie is larger than the two-thirds slice of the second pie. This visual representation provides a concrete understanding of the relative sizes of the fractions.
Method 4: Cross-Multiplication
This method offers a quick way to compare fractions without finding a common denominator. It involves cross-multiplying the numerators and denominators:
-
Cross-multiply: Multiply the numerator of the first fraction by the denominator of the second fraction (3 x 3 = 9). Then, multiply the numerator of the second fraction by the denominator of the first fraction (2 x 4 = 8).
-
Compare the Products: Compare the two products. Since 9 > 8, the fraction with the larger product (3/4) is the greater fraction.
This method provides a concise and efficient way to compare fractions, especially when dealing with larger numbers.
Addressing Common Misconceptions
A common misconception is assuming that because the numerator of 2/3 is closer to the denominator than the numerator of 3/4 is to its denominator, 2/3 is somehow larger. This is incorrect. The relationship between the numerator and the denominator is not the sole determining factor when comparing fractions. We must consider the overall value represented by the fraction.
Another common error is simply comparing numerators or denominators in isolation. Comparing numerators directly only works if the denominators are the same. Similarly, comparing denominators directly only tells us about the size of the pieces, not the number of pieces being considered.
Real-World Applications of Fraction Comparison
The ability to compare fractions is crucial in numerous real-world scenarios:
- Cooking and Baking: Following recipes often requires understanding and comparing fractions to ensure accurate measurements.
- Construction and Engineering: Precise measurements and calculations involving fractions are essential for accurate construction and engineering projects.
- Finance: Calculating percentages, interest rates, and proportions often involves working with fractions.
- Data Analysis: Interpreting data represented in fractional form requires the ability to compare and analyze different fractions.
Conclusion
The answer to the question "Is 3/4 greater than 2/3?" is a resounding yes. We've explored multiple methods—finding a common denominator, converting to decimals, visual representation, and cross-multiplication—to demonstrate this definitively. Understanding these methods provides a strong foundation for working with fractions in various contexts. Mastering fraction comparison is not just about getting the right answer; it's about developing a deeper understanding of mathematical principles and their practical applications in the real world. The ability to confidently compare and manipulate fractions is a critical skill that extends far beyond the classroom and into numerous aspects of everyday life. Remember to practice regularly, utilizing different methods to solidify your understanding and build confidence in your mathematical abilities.
Latest Posts
Latest Posts
-
Summary Of Crucible Act 2
Sep 24, 2025
-
The Giver Book Chapter 1
Sep 24, 2025
-
What Is A Selective Pressure
Sep 24, 2025
-
What Is A Revenue Bill
Sep 24, 2025
-
Does Plasma Have Definite Volume
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about Is 3/4 Greater Than 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.