Is 1/4 Greater Than 1/2
scising
Sep 13, 2025 · 5 min read
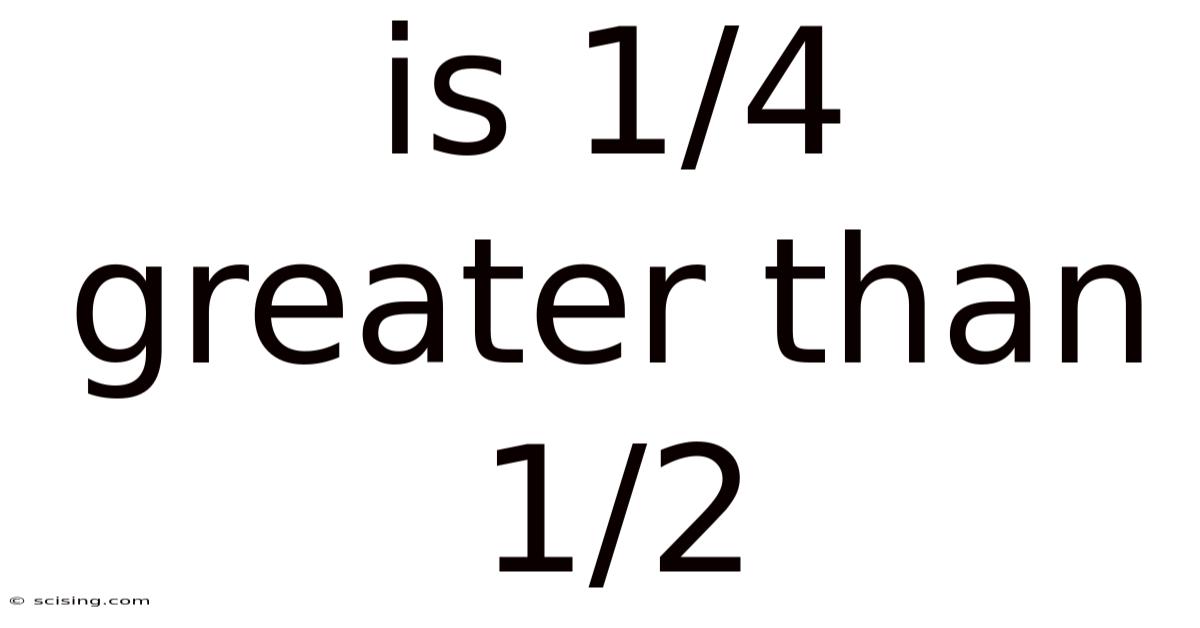
Table of Contents
Is 1/4 Greater Than 1/2? Understanding Fractions and Comparisons
Is 1/4 greater than 1/2? The answer is a resounding no. This seemingly simple question actually provides a fantastic opportunity to delve into the fundamental concepts of fractions, comparison methods, and mathematical reasoning. Understanding fractions is crucial for everyday life, from cooking and budgeting to more advanced mathematical concepts. This article will not only answer the core question but also explore the underlying principles in a clear, comprehensive, and engaging manner.
Introduction to Fractions
Before we tackle the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two key parts:
- Numerator: The top number represents how many parts we have.
- Denominator: The bottom number indicates the total number of equal parts the whole is divided into.
For example, in the fraction 1/2, the numerator (1) signifies that we have one part, and the denominator (2) indicates that the whole is divided into two equal parts. Similarly, in 1/4, we have one part out of a total of four equal parts.
Visualizing Fractions: The Power of Representation
Visual aids are incredibly helpful when working with fractions. Imagine a pizza cut into two equal slices. 1/2 represents one of those slices. Now imagine the same pizza cut into four equal slices. 1/4 represents only one of those smaller slices. Clearly, one half of the pizza is larger than one-quarter.
We can also use other visuals like bars or circles divided into equal sections to represent fractions. This visual approach makes it intuitive to understand which fraction is larger or smaller. Trying this yourself with different drawings is a great way to solidify your understanding.
Comparing Fractions: Methods and Techniques
There are several ways to compare fractions:
-
Visual Comparison: As discussed above, using diagrams can provide a clear visual representation, making it easy to see which fraction is larger.
-
Common Denominator Method: This is a more formal and reliable method. To compare fractions, we need to find a common denominator – a number that is a multiple of both denominators. Once we have a common denominator, we can directly compare the numerators.
Let's compare 1/4 and 1/2 using this method:
-
Find a common denominator: The least common multiple (LCM) of 4 and 2 is 4.
-
Convert the fractions:
- 1/2 remains 1/2 (We can think of this as 2/4, because 2/4 is equivalent to 1/2).
- 1/4 remains 1/4
-
Compare the numerators: Now that both fractions have the same denominator (4), we can compare the numerators: 2 > 1. Therefore, 2/4 (or 1/2) is greater than 1/4.
- Cross-Multiplication: Another efficient method involves cross-multiplication. We multiply the numerator of one fraction by the denominator of the other, and vice versa. The larger product corresponds to the larger fraction.
Let's compare 1/4 and 1/2 using cross-multiplication:
-
Cross-multiply:
- 1 (numerator of 1/4) * 2 (denominator of 1/2) = 2
- 1 (numerator of 1/2) * 4 (denominator of 1/4) = 4
-
Compare the products: 4 > 2. Therefore, 1/2 is greater than 1/4.
Why 1/4 is Smaller Than 1/2: A Deeper Dive
The core reason why 1/4 is smaller than 1/2 lies in the meaning of the denominator. The denominator dictates the size of each individual part. A denominator of 2 means the whole is divided into two larger parts. A denominator of 4 means the whole is divided into four smaller parts. Since each part in 1/4 is smaller than each part in 1/2, one of those smaller parts (1/4) will naturally be less than one of the larger parts (1/2).
Think of it like sharing a cake: Would you rather have 1/2 of a cake or 1/4 of the same cake? Obviously, 1/2 is a larger portion.
Extending the Concept: Comparing More Complex Fractions
The methods discussed above can be applied to more complex fractions as well. For example, let's compare 3/5 and 2/3:
-
Find a common denominator: The LCM of 5 and 3 is 15.
-
Convert the fractions:
- 3/5 = 9/15 (3 x 3 / 5 x 3)
- 2/3 = 10/15 (2 x 5 / 3 x 5)
-
Compare the numerators: 10 > 9. Therefore, 2/3 is greater than 3/5.
Or using cross-multiplication:
-
Cross-multiply:
- 3 * 3 = 9
- 2 * 5 = 10
-
Compare the products: 10 > 9. Therefore, 2/3 is greater than 3/5.
Frequently Asked Questions (FAQ)
Q: What if the fractions have the same numerator?
A: If two fractions have the same numerator, the fraction with the smaller denominator is the larger fraction. For example, 1/3 > 1/5 because each part in 1/3 is larger than each part in 1/5.
Q: Are there any other ways to compare fractions?
A: Yes, you can also convert fractions to decimals. To compare 1/4 and 1/2, convert them to decimals: 1/4 = 0.25 and 1/2 = 0.5. Since 0.5 > 0.25, 1/2 > 1/4. However, the common denominator method and cross-multiplication are generally preferred for their simplicity and efficiency.
Q: Why is understanding fractions important?
A: Fractions are fundamental to many areas of mathematics and real-world applications. They're crucial for understanding percentages, ratios, proportions, and more advanced concepts like algebra and calculus. Daily life applications include measuring ingredients for cooking, dividing expenses, and understanding discounts.
Conclusion: Mastering Fractions for a Brighter Future
In conclusion, 1/4 is definitively not greater than 1/2. This seemingly straightforward comparison allows us to explore the core principles of fractions, emphasizing the importance of understanding numerators, denominators, and various comparison methods. By mastering these concepts, you equip yourself with essential skills applicable to various mathematical disciplines and everyday situations. Remember, visualizing fractions, whether through diagrams or real-world examples, significantly aids comprehension. Practice comparing fractions using different methods to enhance your understanding and build a strong foundation in mathematics. The ability to confidently work with fractions will undoubtedly benefit you in your academic pursuits and beyond.
Latest Posts
Latest Posts
-
What Is A 19 25 Grade
Sep 13, 2025
-
Formula For Average Tax Rate
Sep 13, 2025
-
Probability Of A Simple Event
Sep 13, 2025
-
What Is 3 Of 180000
Sep 13, 2025
-
Tertiary Consumers In The Tundra
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Is 1/4 Greater Than 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.