Is 1/2 More Than 1/3
scising
Sep 05, 2025 · 6 min read
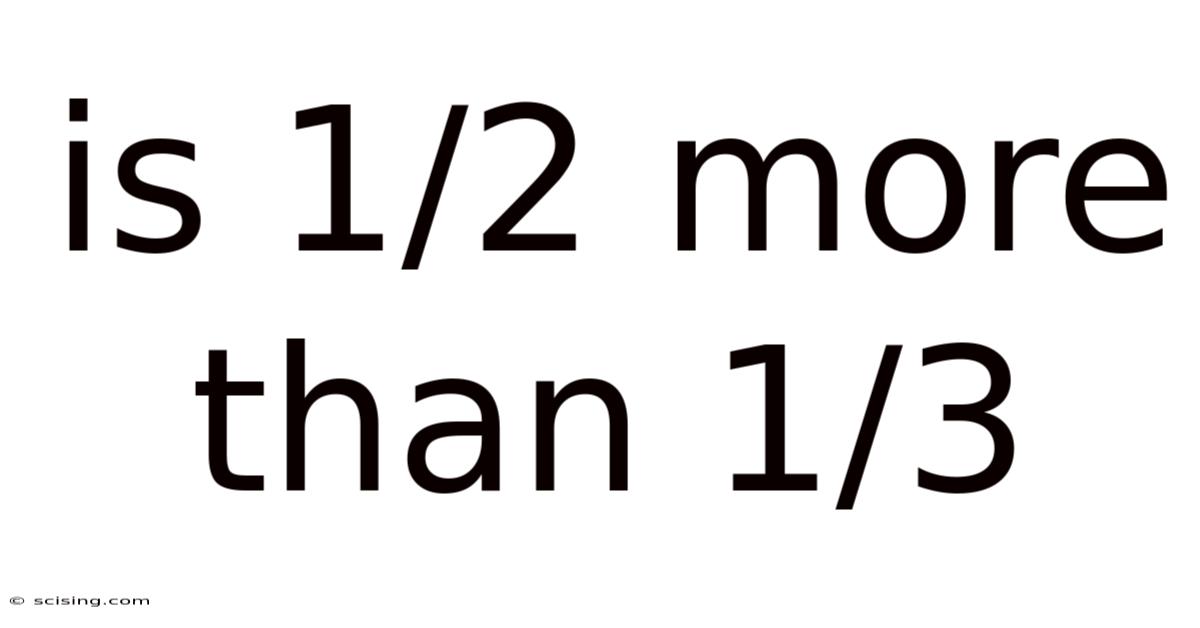
Table of Contents
Is 1/2 More Than 1/3? A Deep Dive into Fractions and Comparisons
Understanding fractions is fundamental to mathematics and everyday life. This article will explore the question, "Is 1/2 more than 1/3?", providing a comprehensive explanation accessible to all, from elementary school students to adults looking to refresh their foundational math skills. We'll go beyond a simple yes or no answer, delving into the concepts behind fraction comparison, offering various methods to solve such problems, and exploring real-world applications.
Introduction: Understanding Fractions
A fraction represents a part of a whole. It's written as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator shows how many of those parts we're considering. For example, in the fraction 1/2, the whole is divided into two equal parts, and we're looking at one of those parts. Similarly, 1/3 represents one out of three equal parts.
Comparing Fractions: Visual Representation
The easiest way to compare 1/2 and 1/3 is through visualization. Imagine two identical pizzas.
- Pizza 1: Cut into two equal slices. Each slice represents 1/2 of the pizza.
- Pizza 2: Cut into three equal slices. Each slice represents 1/3 of the pizza.
Looking at the pizzas, it's immediately apparent that one slice from Pizza 1 (1/2) is larger than one slice from Pizza 2 (1/3). Therefore, yes, 1/2 is more than 1/3.
Comparing Fractions: Finding a Common Denominator
Visual representation works well for simple fractions, but for more complex comparisons, a more robust method is needed. This involves finding a common denominator. A common denominator is a number that is a multiple of both denominators. For 1/2 and 1/3, the least common denominator (LCD) is 6 (2 x 3 = 6).
- Convert 1/2: To get a denominator of 6, we multiply both the numerator and the denominator by 3: (1 x 3) / (2 x 3) = 3/6
- Convert 1/3: To get a denominator of 6, we multiply both the numerator and the denominator by 2: (1 x 2) / (3 x 2) = 2/6
Now we compare 3/6 and 2/6. Since 3 is greater than 2, 3/6 is greater than 2/6. Therefore, 1/2 is greater than 1/3. This method ensures accuracy and can be applied to any fraction comparison.
Comparing Fractions: Cross-Multiplication
Another efficient method for comparing fractions is cross-multiplication. This technique is particularly useful when finding a common denominator is less straightforward.
To compare 1/2 and 1/3 using cross-multiplication:
- Multiply the numerator of the first fraction (1) by the denominator of the second fraction (3): 1 x 3 = 3
- Multiply the numerator of the second fraction (1) by the denominator of the first fraction (2): 1 x 2 = 2
- Compare the results: 3 > 2. Since the result of multiplying the numerator of the first fraction by the denominator of the second fraction is larger, the first fraction (1/2) is larger.
This method provides a quick and reliable way to compare fractions without the need for finding a common denominator.
The Decimal Equivalent: A Numerical Comparison
Converting fractions to decimals offers another perspective.
- 1/2: 1 divided by 2 = 0.5
- 1/3: 1 divided by 3 = 0.333... (a repeating decimal)
Comparing 0.5 and 0.333..., it's evident that 0.5 (1/2) is greater than 0.333... (1/3).
This method is helpful for visualizing the magnitude of the fractions, particularly when dealing with fractions that aren't easily comparable visually or through common denominators.
Beyond 1/2 and 1/3: Generalizing Fraction Comparison
The principles discussed above apply to comparing any two fractions. The key is to find a common denominator or use cross-multiplication to determine which fraction represents a larger portion of the whole. Remember, the larger the numerator relative to the denominator, the larger the fraction's value.
For example, let's compare 5/8 and 3/4:
- Common Denominator Method: The LCD is 8. 3/4 becomes 6/8. Since 6/8 > 5/8, 3/4 > 5/8.
- Cross-Multiplication Method: (5 x 4) = 20 and (3 x 8) = 24. Since 20 < 24, 5/8 < 3/4.
Real-World Applications of Fraction Comparison
Understanding fraction comparison is crucial in various real-world scenarios:
- Cooking and Baking: Following recipes often involves understanding ratios and fractions. Knowing if 1/2 cup is more than 1/3 cup is essential for accurate measurements.
- Construction and Engineering: Precision in measurements is paramount. Comparing fractions is necessary for calculating dimensions and quantities accurately.
- Finance and Budgeting: Managing finances involves dealing with percentages and fractions. Understanding fraction comparison helps in making informed financial decisions.
- Data Analysis: Interpreting data often involves working with fractions and proportions. The ability to compare fractions is crucial for drawing accurate conclusions from data.
Frequently Asked Questions (FAQ)
Q: Is there a shortcut to compare fractions with the same numerator?
A: Yes. If two fractions have the same numerator, the fraction with the smaller denominator is larger. For example, 2/5 > 2/7 because fifths are larger than sevenths.
Q: How do I compare fractions with different numerators and denominators?
A: Use the common denominator method or cross-multiplication method, as explained above.
Q: What if I get a negative fraction? How do I compare them?
A: When dealing with negative fractions, remember that the magnitude of the negative fraction still follows the same rules as above. However, the smaller the negative number, the larger its value. For example, -1/2 > -2/3. The negative one-half is closer to zero and thus larger than negative two-thirds.
Q: Can I use a calculator to compare fractions?
A: Yes, you can convert the fractions to decimals using a calculator and compare the decimal values. However, understanding the underlying principles of fraction comparison is still important for solving problems without a calculator and for developing mathematical intuition.
Conclusion: Mastering Fraction Comparison
The question, "Is 1/2 more than 1/3?", serves as a springboard to understanding the broader concept of fraction comparison. This article explored various methods for comparing fractions, emphasizing the importance of visual representation, finding common denominators, cross-multiplication, and converting to decimals. Mastering these techniques is essential not only for academic success but also for navigating numerous practical situations in everyday life. Remember that the key is to develop a robust understanding of the underlying principles rather than just memorizing algorithms; this approach fosters true mathematical fluency and empowers you to confidently tackle fraction comparisons and other mathematical challenges. By understanding the concepts explained here, you'll be well-equipped to confidently handle fractions and their comparisons in any context.
Latest Posts
Latest Posts
-
The Outsider Stephen King Summary
Sep 05, 2025
-
Grand Coulee Dam Visitor Center
Sep 05, 2025
-
4 Adjectives To Describe Pythagoras
Sep 05, 2025
-
Antiderivatives Of Inverse Trig Functions
Sep 05, 2025
-
Sodapop Curtis From The Outsiders
Sep 05, 2025
Related Post
Thank you for visiting our website which covers about Is 1/2 More Than 1/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.