Is 1/2 Greater Than 5/8
scising
Sep 06, 2025 · 5 min read
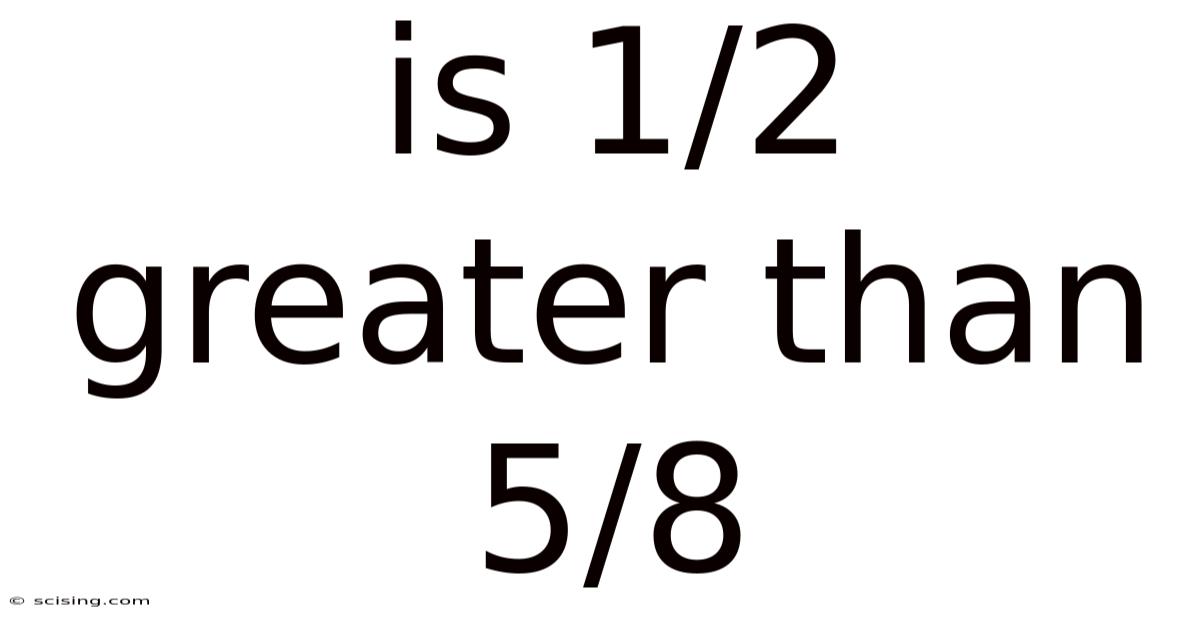
Table of Contents
Is 1/2 Greater Than 5/8? A Deep Dive into Fraction Comparison
Understanding fractions is fundamental to mathematics, and comparing them is a crucial skill. This article will thoroughly explore the question: "Is 1/2 greater than 5/8?" We'll not only answer this specific question but also delve into the various methods for comparing fractions, ensuring you develop a solid grasp of the concept. This will cover everything from basic visual representations to more advanced techniques, providing a comprehensive understanding suitable for learners of all levels.
Introduction: Understanding Fractions
Before we tackle the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a/b, where 'a' is the numerator (the number of parts we have) and 'b' is the denominator (the total number of equal parts the whole is divided into). For example, in the fraction 1/2, 1 represents the number of parts we have, and 2 represents the total number of equal parts the whole is divided into.
This understanding is crucial because it forms the basis for all fraction comparison methods.
Method 1: Visual Representation
One of the easiest ways to compare fractions is through visual representation. Imagine a pizza.
- 1/2: If we cut the pizza into two equal slices, 1/2 represents one of those slices.
- 5/8: If we cut the same pizza into eight equal slices, 5/8 represents five of those slices.
By visualizing, it becomes apparent that five slices out of eight (5/8) are larger than one slice out of two (1/2). This simple visual method provides an intuitive understanding of the relative sizes of the fractions.
Method 2: Finding a Common Denominator
This is a more formal and widely used method for comparing fractions. The core principle is to rewrite the fractions so they have the same denominator. This allows for a direct comparison of their numerators.
Let's compare 1/2 and 5/8 using this method:
-
Find the least common multiple (LCM) of the denominators: The denominators are 2 and 8. The LCM of 2 and 8 is 8.
-
Rewrite the fractions with the common denominator:
-
To change 1/2 to have a denominator of 8, we multiply both the numerator and the denominator by 4: (1 x 4) / (2 x 4) = 4/8
-
5/8 already has a denominator of 8, so it remains unchanged.
-
-
Compare the numerators: Now we compare 4/8 and 5/8. Since 4 < 5, we conclude that 4/8 < 5/8.
Therefore, 1/2 (which is equivalent to 4/8) is not greater than 5/8.
Method 3: Converting to Decimals
Another effective method involves converting the fractions into decimals. This provides a numerical comparison that's easy to understand.
-
Convert 1/2 to a decimal: Divide the numerator (1) by the denominator (2): 1 ÷ 2 = 0.5
-
Convert 5/8 to a decimal: Divide the numerator (5) by the denominator (8): 5 ÷ 8 = 0.625
-
Compare the decimals: Now we compare 0.5 and 0.625. Since 0.5 < 0.625, we conclude that 1/2 is less than 5/8.
Method 4: Cross-Multiplication
This is a shortcut method that directly compares fractions without finding a common denominator.
-
Cross-multiply: Multiply the numerator of the first fraction by the denominator of the second fraction, and vice versa.
- 1/2 and 5/8: (1 x 8) = 8 and (2 x 5) = 10
-
Compare the products: Compare the two products. The fraction with the larger product is the larger fraction.
- Since 8 < 10, we conclude that 1/2 < 5/8.
Why Understanding Fraction Comparison is Important
Mastering fraction comparison is essential for various reasons:
-
Everyday Applications: From cooking (following recipes) to building (measuring materials) and managing finances (calculating percentages), understanding fractions is crucial in our daily lives. Comparing fractions allows us to determine which quantity is larger or smaller.
-
Further Mathematical Studies: Fraction comparison forms the foundation for more advanced mathematical concepts like algebra, geometry, and calculus. A strong understanding of fractions is vital for success in these areas.
-
Problem-Solving Skills: Comparing fractions hones problem-solving skills. It teaches us to analyze, strategize, and find efficient solutions. This skill transcends mathematics and applies to many aspects of life.
-
Critical Thinking: The process of comparing fractions encourages critical thinking. We need to analyze the given information, choose appropriate methods, and interpret the results correctly. This develops our analytical and reasoning abilities.
Frequently Asked Questions (FAQ)
Q1: Can I always use the common denominator method?
A1: Yes, the common denominator method is a reliable and universally applicable method for comparing any two fractions. While other methods might be quicker in some cases, the common denominator method always provides an accurate comparison.
Q2: Which method is the fastest?
A2: The fastest method often depends on the specific fractions being compared. For simple fractions, visual representation or cross-multiplication might be quicker. For more complex fractions, the decimal conversion or common denominator method might be more efficient.
Q3: What if the fractions have the same denominator?
A3: If the fractions have the same denominator, simply compare their numerators. The fraction with the larger numerator is the larger fraction.
Q4: What if the fractions have the same numerator but different denominators?
A4: If the fractions have the same numerator but different denominators, the fraction with the smaller denominator is the larger fraction. This is because a smaller denominator means the whole is divided into fewer parts, making each part larger.
Conclusion: 1/2 is not greater than 5/8
Through visual representation, finding a common denominator, converting to decimals, and cross-multiplication, we have conclusively shown that 1/2 is not greater than 5/8. 5/8 is larger than 1/2. Understanding the different methods for comparing fractions is crucial for developing a robust understanding of mathematical concepts and their practical applications. Remember to choose the method that feels most comfortable and efficient for you, but always double-check your work! Practice is key to mastering this essential skill. The more you work with fractions, the more intuitive and effortless the comparison will become. Don't be afraid to explore different methods and find the one that best suits your learning style.
Latest Posts
Latest Posts
-
Notes On Treble Clef Staff
Sep 06, 2025
-
Social Cognitive Theory Of Personality
Sep 06, 2025
-
1 3 Is A Rational Number
Sep 06, 2025
-
Lewis Dot Structure For H
Sep 06, 2025
-
Sample Of Screw Simple Machine
Sep 06, 2025
Related Post
Thank you for visiting our website which covers about Is 1/2 Greater Than 5/8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.