Four Times What Equals 100
scising
Sep 13, 2025 · 5 min read
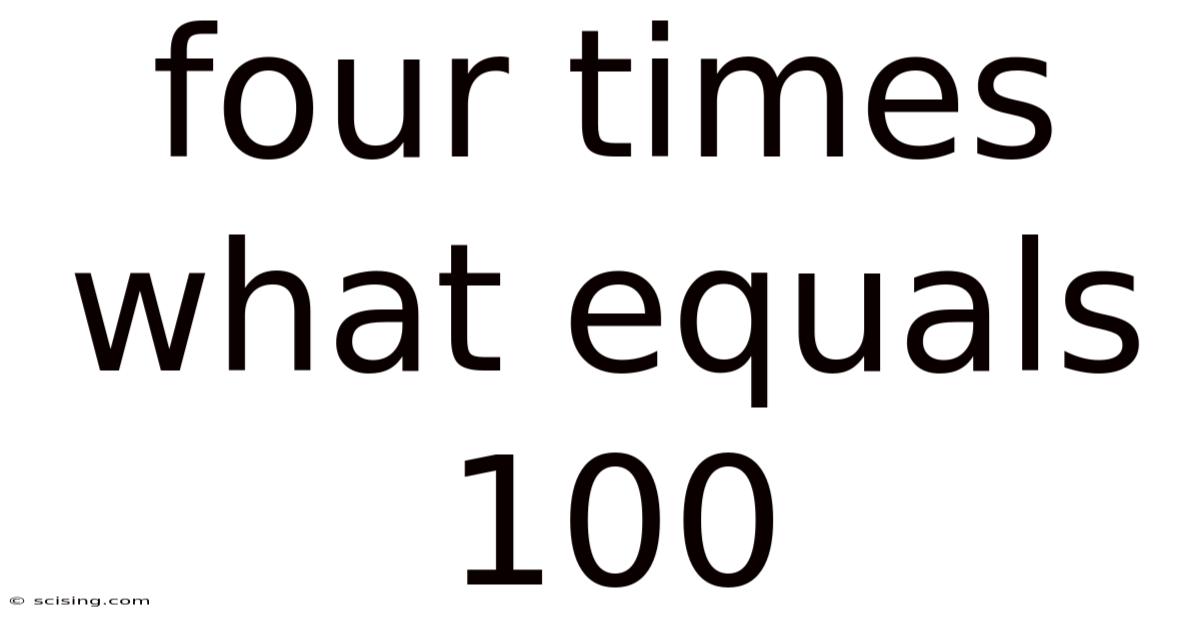
Table of Contents
Four Times What Equals 100? Unlocking the Power of Multiplication and Problem Solving
This article explores the seemingly simple question: "Four times what equals 100?" While the answer might seem immediately obvious to some, delving into this problem unveils a wealth of mathematical concepts and problem-solving strategies applicable across various fields. We'll journey from the basic arithmetic solution to exploring more advanced methods, examining the underlying principles of multiplication, and even touching upon real-world applications. This in-depth exploration aims to provide a comprehensive understanding not just of the answer, but of the process itself.
Finding the Solution: Basic Arithmetic
The most straightforward approach to solving "Four times what equals 100?" involves basic division. We can represent the problem as an algebraic equation:
4 * x = 100
Where 'x' represents the unknown number we're trying to find. To solve for 'x', we simply divide both sides of the equation by 4:
x = 100 / 4
This gives us the answer:
x = 25
Therefore, four times 25 equals 100. This is the fundamental solution, easily grasped by anyone with a basic understanding of arithmetic.
Beyond the Basics: Exploring Different Approaches
While the division method is the most efficient, exploring alternative methods can enhance our understanding of the problem and its underlying mathematical principles.
Using Repeated Subtraction
Instead of division, we can use repeated subtraction to find the solution. We start with 100 and repeatedly subtract 4 until we reach zero. The number of times we subtract 4 represents the value of 'x'.
100 - 4 = 96 96 - 4 = 92 92 - 4 = 88 ...and so on until we reach 0.
Counting the number of times we subtracted 4 would give us the answer, 25. This method, although more time-consuming, illustrates the inverse relationship between multiplication and subtraction.
Visual Representation: Using Arrays and Models
Visual aids can make abstract mathematical concepts more concrete and accessible. We can represent the problem using an array. Imagine a rectangle with four rows. The total area of the rectangle represents 100. To find the number of columns (our 'x'), we can visualize dividing the rectangle into four equal sections. Each section would have an area of 25, thus giving us our answer.
Similarly, we could use blocks or counters to build a model. We would group the counters into sets of four until we use all 100 counters. The number of groups would again represent 'x', which is 25.
The Mathematical Principles at Play
The problem "Four times what equals 100?" inherently involves the fundamental principles of:
-
Multiplication: The core operation is multiplication, which represents repeated addition. In this case, it's 4 added to itself 25 times.
-
Division: Solving the equation requires division, the inverse operation of multiplication. Division breaks a quantity into equal parts.
-
Inverse Operations: Multiplication and division are inverse operations, meaning they "undo" each other. This principle is crucial in solving algebraic equations.
-
Algebra: Representing the problem as an algebraic equation (4 * x = 100) introduces the power of algebraic manipulation. We can use algebraic rules to isolate the variable 'x' and find its value.
Real-World Applications: Where This Problem Matters
The simple problem of "Four times what equals 100?" might seem isolated, but its underlying principles are applied extensively in numerous real-world scenarios:
-
Unit Conversions: Converting units (e.g., inches to feet, kilograms to pounds) often involves multiplication or division.
-
Budgeting and Finance: Calculating percentages, determining the cost per item, or dividing a budget across different categories utilizes similar mathematical reasoning.
-
Engineering and Construction: Calculating material quantities, determining structural dimensions, or scaling blueprints all involve proportions and ratios, fundamentally based on multiplication and division.
-
Data Analysis: Working with datasets, calculating averages, and determining proportions all involve similar arithmetic operations.
-
Everyday Life: Sharing costs equally among friends, calculating the number of items needed, or dividing a recipe to serve fewer people are common examples.
Extending the Concept: Variations and Challenges
Once we understand the basic solution, we can explore variations and more challenging problems:
-
Different Multipliers: Instead of 4, we could use other multipliers. For example, "Five times what equals 100?" would be solved using the same principles, but with a different divisor (100/5 = 20).
-
Larger Numbers: We can increase the scale of the problem, using larger numbers and exploring more complex calculations.
-
Word Problems: The same mathematical principles are applied in word problems that require solving for an unknown quantity. For example, "A baker made 100 cookies and wants to package them into boxes of 4 cookies each. How many boxes does he need?"
-
Equations with Multiple Operations: More complex equations might involve multiple operations (addition, subtraction, multiplication, division) and require a step-by-step approach to solve for the unknown variable.
Frequently Asked Questions (FAQ)
Q: What if the number 100 was different? How would the process change?
A: The process remains the same. If the equation was, for example, "4 * x = 120", you would simply divide 120 by 4 to find 'x' (x = 30). The principle of dividing the total by the multiplier remains constant.
Q: Can this be solved without division?
A: Yes, as demonstrated earlier, repeated subtraction can be used, although it's less efficient for larger numbers. Visual methods like arrays and models also offer alternative approaches.
Q: Why is division the most efficient method?
A: Division directly provides the answer in a single step. Repeated subtraction or visual methods can be time-consuming, especially when dealing with large numbers.
Q: What are some common mistakes students make when solving similar problems?
A: Common mistakes include performing the incorrect operation (addition instead of division), misplacing the decimal point when dealing with decimals, and not understanding the inverse relationship between multiplication and division.
Conclusion: Mastering the Fundamentals
The simple question, "Four times what equals 100?" provides a springboard for exploring fundamental mathematical concepts. Understanding the solution and the various methods to arrive at the answer reinforces the importance of multiplication, division, inverse operations, and algebraic thinking. These principles are crucial not just in academic settings but also in navigating countless real-world situations. By mastering these basic concepts, we build a solid foundation for tackling more complex mathematical challenges and problem-solving scenarios in any field. The journey to understanding this seemingly simple equation unlocks a world of mathematical possibilities.
Latest Posts
Latest Posts
-
What Shape Has Nine Sides
Sep 13, 2025
-
What Percent Is 7 12
Sep 13, 2025
-
Food Chains In A Rainforest
Sep 13, 2025
-
Real Life Exponential Growth Examples
Sep 13, 2025
-
When Is Huckleberry Finn Set
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Four Times What Equals 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.