Force Equals Pressure Times Area
scising
Sep 13, 2025 · 7 min read
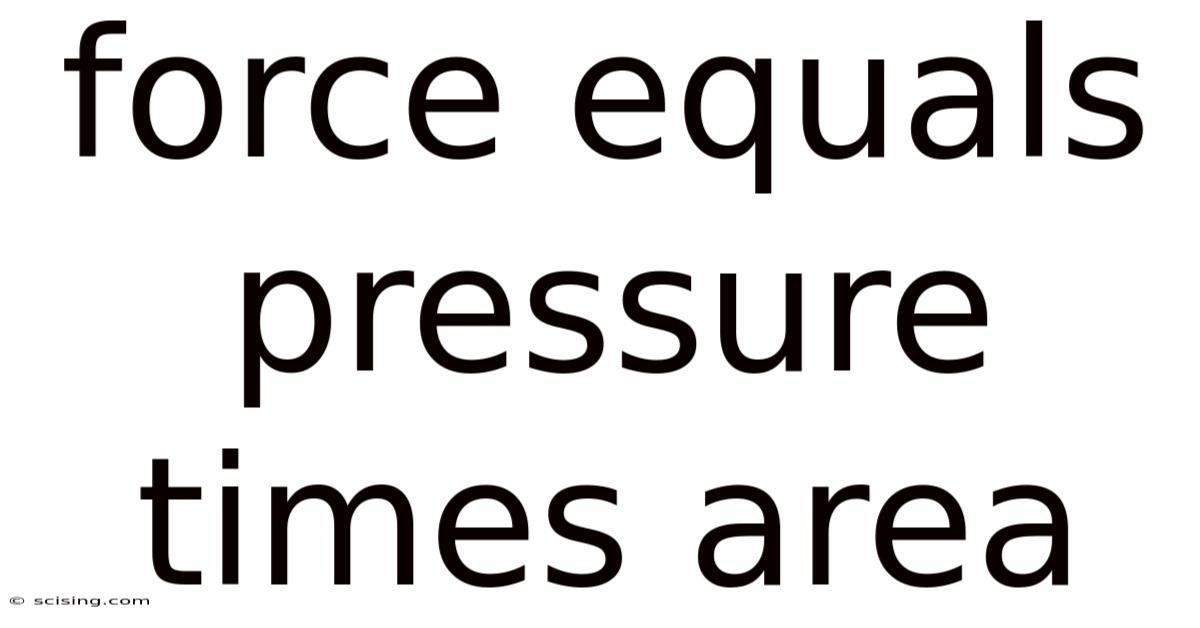
Table of Contents
Force, Pressure, and Area: Understanding the Fundamental Relationship
The simple equation, Force = Pressure x Area, underpins countless phenomena in our world, from the subtle pressure of air on our skin to the immense forces generated by hydraulic systems. Understanding this relationship is crucial for fields ranging from engineering and physics to everyday life situations. This article will delve deep into the meaning of this equation, exploring its applications, implications, and providing illustrative examples to solidify your understanding.
What is Force?
In physics, force is defined as an interaction that, when unopposed, will change the motion of an object. This change can involve a change in speed, direction, or both. Force is a vector quantity, meaning it possesses both magnitude (how strong the force is) and direction. We measure force in Newtons (N). A Newton is the force required to accelerate a mass of one kilogram at a rate of one meter per second squared (1 N = 1 kg⋅m/s²). Think of pushing a heavy box across the floor – you are applying a force to overcome friction and inertia.
What is Pressure?
Pressure is defined as the force applied perpendicularly to a surface per unit area. It describes how concentrated a force is over a given region. Imagine pressing a thumbtack into a corkboard. While the force you apply might be relatively small, the pressure is immense because the force is concentrated over the tiny area of the thumbtack's point. We express pressure in Pascals (Pa), where one Pascal is equal to one Newton per square meter (1 Pa = 1 N/m²).
What is Area?
Area is the measure of a two-dimensional surface. In the context of the equation Force = Pressure x Area, it refers to the surface area over which the pressure is acting. The units of area are typically square meters (m²), but other units, such as square centimeters (cm²) or square feet (ft²), are also used depending on the context.
Understanding the Equation: Force = Pressure x Area
The equation Force = Pressure x Area eloquently describes the relationship between these three quantities. It states that the total force exerted on a surface is directly proportional to both the pressure applied and the area over which it is applied. This means:
-
If pressure increases, force increases (assuming area remains constant). Imagine inflating a balloon – as the pressure of the air inside increases, so does the outward force on the balloon's surface.
-
If area increases, force increases (assuming pressure remains constant). Think of a wide snowshoe versus a narrow ski. The snowshoe distributes your weight over a larger area, reducing the pressure on the snow and preventing you from sinking. The force exerted on the snow is the same (your weight), but the pressure is significantly less due to the larger area.
-
Conversely, if either pressure or area decreases, the force will also decrease.
Applications of Force = Pressure x Area
This seemingly simple equation has far-reaching applications across numerous disciplines:
-
Hydraulic Systems: Hydraulic systems, such as those found in car brakes and construction equipment, rely heavily on this principle. A small force applied to a small area in a confined liquid creates a large pressure, which is then transmitted to a larger area, resulting in a significantly larger force. This amplification of force is the key to their effectiveness.
-
Pneumatic Systems: Similar to hydraulic systems, pneumatic systems utilize compressed air to generate force. Airbags in cars, for example, deploy rapidly due to the high pressure of the compressed gas expanding over a large area, generating a significant force to cushion the impact.
-
Fluid Mechanics: The equation is fundamental in fluid mechanics, enabling the calculation of forces exerted by fluids on surfaces. This is crucial in designing ships, submarines, and other structures that interact with water or other fluids.
-
Meteorology: Atmospheric pressure exerts a force on everything on Earth. Understanding this pressure and its variation helps meteorologists predict weather patterns and understand the forces that drive wind and storms. The weight of the atmosphere above a given area creates a significant force.
-
Medical Applications: Understanding pressure and force is critical in various medical applications. For instance, the pressure exerted by blood against the walls of arteries is a key indicator of cardiovascular health. Similarly, understanding the pressure distribution in tissues is crucial for designing prosthetic devices and implants.
Illustrative Examples
Let's solidify our understanding with some examples:
Example 1: A Hydraulic Jack
A hydraulic jack uses a small piston with an area of 1 cm² to lift a car. A force of 100 N is applied to the small piston. This force creates a pressure of 100 N/cm². If the large piston has an area of 100 cm², the force exerted on the car will be:
Force = Pressure x Area = (100 N/cm²) x (100 cm²) = 10,000 N
The jack amplifies the force by a factor of 100.
Example 2: Walking on Snow
A person weighing 700 N wears snowshoes with a total contact area of 0.5 m². The pressure exerted on the snow is:
Pressure = Force / Area = 700 N / 0.5 m² = 1400 Pa
If the person were wearing regular shoes with a contact area of 0.01 m², the pressure would be:
Pressure = Force / Area = 700 N / 0.01 m² = 70,000 Pa
The significantly higher pressure with regular shoes would cause the person to sink into the snow.
Example 3: Atmospheric Pressure
Atmospheric pressure at sea level is approximately 101,325 Pa. This means that the atmosphere exerts a force of 101,325 N on every square meter of surface area. Consider a standard-sized window (approximately 1 m²):
Force = Pressure x Area = 101,325 Pa x 1 m² = 101,325 N
This substantial force is constantly acting on the window, yet it doesn't break because the pressure is equalized on both sides.
Explaining the Equation Scientifically
The equation Force = Pressure x Area is a direct consequence of the fundamental definitions of force and pressure. Pressure is defined as force per unit area (P = F/A). Rearranging this equation gives us the familiar Force = Pressure x Area. This relationship holds true for both liquids and gases, assuming the pressure is uniformly distributed across the surface.
The pressure within a fluid (liquid or gas) is determined by the weight of the fluid above a given point. At greater depths, the weight of the fluid column increases, leading to higher pressure. This principle is described by Pascal's Law, which states that a change in pressure applied to an enclosed fluid is transmitted undiminished to every point of the fluid and to the walls of the container.
Frequently Asked Questions (FAQs)
- Q: What if the pressure isn't uniform across the surface?
A: The equation Force = Pressure x Area is most accurate when the pressure is uniform across the surface. If the pressure varies, you would need to integrate the pressure over the entire surface area to find the total force. This involves more advanced calculus.
- Q: Does this equation apply to all types of forces?
A: The equation primarily applies to forces exerted by fluids (liquids and gases) or forces that are perpendicular to a surface. It might not be directly applicable to shear forces or other types of forces that aren't perpendicular to the surface.
- Q: What are the limitations of this equation?
A: While widely applicable, the equation assumes ideal conditions. In reality, factors like friction, deformation of materials, and non-uniform pressure distributions might affect the accuracy of the calculated force.
Conclusion
The equation Force = Pressure x Area is a cornerstone of physics and engineering, providing a concise and powerful way to understand the relationship between force, pressure, and area. Its implications reach far beyond the classroom, influencing the design and operation of numerous systems and technologies. By grasping the fundamental principles behind this equation and its practical applications, you can gain a deeper appreciation for the forces that shape our world. From the subtle pressure of the atmosphere to the immense power of hydraulic systems, this equation illuminates the intricate interplay of these essential physical quantities. Understanding this equation allows for a more profound comprehension of the world around us, fostering innovation and problem-solving across diverse fields.
Latest Posts
Latest Posts
-
Maximum And Minimum Of Parabola
Sep 13, 2025
-
What Is An Evaluation Essay
Sep 13, 2025
-
Is Chf3 Polar Or Nonpolar
Sep 13, 2025
-
Demand Curve Is Downward Sloping
Sep 13, 2025
-
Volume Of Prisms And Pyramids
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Force Equals Pressure Times Area . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.