Divide 1 3 By 2
scising
Sep 21, 2025 · 5 min read
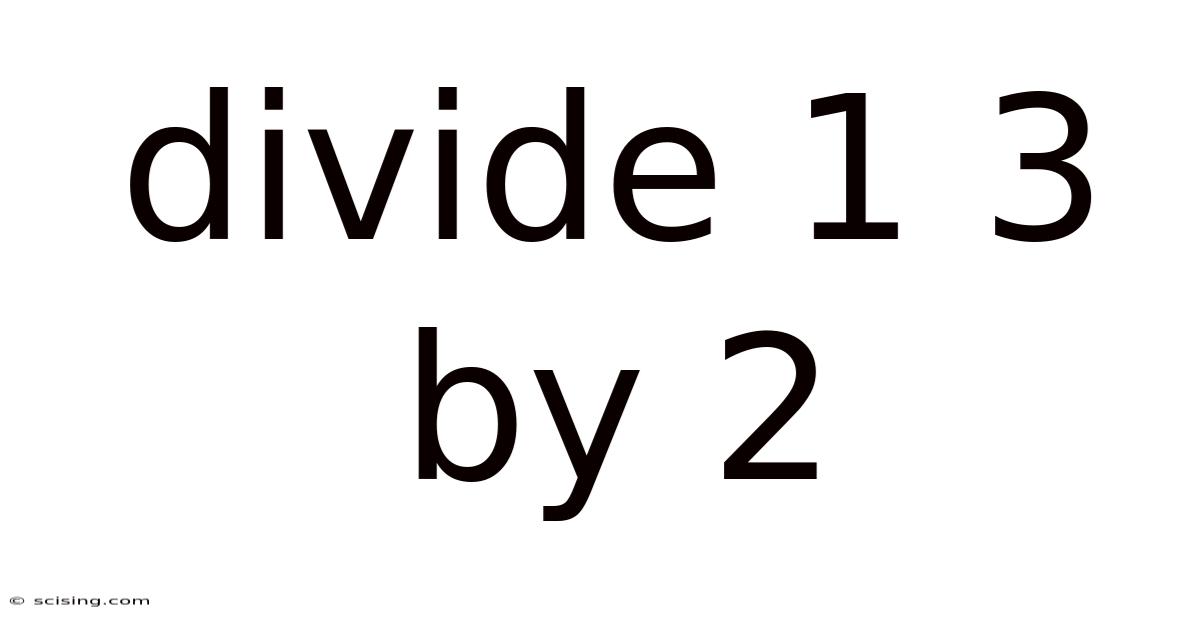
Table of Contents
Diving Deep into the Simple Problem: Dividing 1/3 by 2
This seemingly simple arithmetic problem, dividing 1/3 by 2, often trips up students and even adults who haven't actively engaged with fractions in a while. Understanding how to solve this, and similar problems, is crucial for building a strong foundation in mathematics. This article will not only provide the solution but delve into the underlying concepts, exploring different approaches, and offering insights to improve your fractional arithmetic skills. We will unravel the mystery of dividing fractions and equip you with the knowledge to tackle more complex problems with confidence.
Understanding Fractions: A Quick Refresher
Before we jump into dividing 1/3 by 2, let's refresh our understanding of fractions. A fraction represents a part of a whole. It consists of two parts:
- Numerator: The top number, representing the number of parts we have.
- Denominator: The bottom number, representing the total number of equal parts the whole is divided into.
For example, in the fraction 1/3, the numerator (1) tells us we have one part, and the denominator (3) tells us the whole is divided into three equal parts.
Method 1: The "Keep, Change, Flip" Method (for Division of Fractions)
This is arguably the most popular and easiest method for dividing fractions. The process involves three steps:
- Keep: Keep the first fraction as it is (1/3).
- Change: Change the division sign (÷) to a multiplication sign (×).
- Flip: Flip the second fraction (2 can be written as 2/1; flipping it gives 1/2).
Applying this to our problem:
1/3 ÷ 2 becomes 1/3 × 1/2
Now, multiply the numerators together and the denominators together:
(1 × 1) / (3 × 2) = 1/6
Therefore, 1/3 divided by 2 equals 1/6.
Method 2: Using the Reciprocal
This method builds upon the understanding of reciprocals. The reciprocal of a number is simply 1 divided by that number. For example, the reciprocal of 2 is 1/2, and the reciprocal of 1/3 is 3/1 (or simply 3).
Dividing by a number is the same as multiplying by its reciprocal. So, dividing 1/3 by 2 is equivalent to multiplying 1/3 by the reciprocal of 2:
1/3 ÷ 2 = 1/3 × 1/2 = 1/6
This method reinforces the fundamental concept behind the "keep, change, flip" method.
Method 3: Visual Representation
Visualizing the problem can be particularly helpful for grasping the concept. Imagine a pizza cut into three equal slices. 1/3 represents one of these slices. Dividing this slice by 2 means splitting that single slice into two equal parts. Each of these new smaller parts represents 1/6 of the whole pizza.
This visual approach helps solidify the understanding that dividing a fraction by a whole number results in a smaller fraction.
A Deeper Dive into the Mathematics: Why Does "Keep, Change, Flip" Work?
The "keep, change, flip" method is a shortcut, but understanding the underlying mathematics is essential for true comprehension. Let's explore this using a more general example:
a/b ÷ c/d
We can rewrite this division problem as a fraction:
(a/b) / (c/d)
To simplify a complex fraction (a fraction within a fraction), we multiply the numerator by the reciprocal of the denominator:
(a/b) × (d/c) = (a × d) / (b × c)
This demonstrates why the "keep, change, flip" method works. It's a streamlined process that directly implements the rule for simplifying complex fractions.
Expanding on the Concept: Dividing Fractions by Fractions
The principles discussed above apply equally to dividing a fraction by another fraction. Let's consider an example:
1/3 ÷ 1/2
Using the "keep, change, flip" method:
1/3 × 2/1 = 2/3
In this case, dividing 1/3 by 1/2 results in a larger fraction (2/3) because we're dividing by a fraction less than 1.
Practical Applications: Where Do We Use Fractional Division?
Fractional division isn't just an abstract mathematical concept; it has numerous real-world applications. Consider these examples:
- Baking: Recipes often require dividing ingredients. If a recipe calls for 1/3 cup of sugar and you want to halve the recipe, you need to divide 1/3 by 2.
- Sewing: Cutting fabric requires precise measurements. Dividing fabric lengths involves fractions.
- Construction: Many construction projects require accurate fractional measurements for materials and dimensions.
- Engineering: Engineers regularly use fractions and fractional division in designing and building structures.
Frequently Asked Questions (FAQ)
Q: Can I divide 1/3 by 2 using decimals?
A: Yes, you can. First, convert 1/3 to its decimal equivalent (approximately 0.333...). Then, divide 0.333... by 2, which gives approximately 0.1666... However, this approach might lead to rounding errors, making the fractional method more precise.
Q: What if I have a mixed number (e.g., 1 1/3)?
A: Convert the mixed number to an improper fraction first. For example, 1 1/3 is equivalent to 4/3. Then apply the "keep, change, flip" method or the reciprocal method as described above.
Q: Is there a different way to explain the “Keep, Change, Flip” rule?
A: Another way to visualize it is to think of dividing as asking "how many times does the second fraction fit into the first?" Flipping the second fraction and multiplying essentially answers that question.
Q: Why is it important to master fraction division?
A: A solid understanding of fraction division is critical for building a strong mathematical foundation. This skill is essential for further studies in algebra, calculus, and other advanced mathematical concepts. It also has practical applications in many everyday scenarios.
Conclusion: Mastering Fractions for a Brighter Future
Dividing 1/3 by 2, while seemingly simple, opens a door to a deeper understanding of fractional arithmetic. By mastering this fundamental concept, you not only solve this specific problem but also equip yourself with the tools to tackle more complex fractional calculations. Remember the "keep, change, flip" method or the reciprocal method; visualize the problem if needed; and don't hesitate to practice. The more you practice, the more confident and proficient you'll become in handling fractions, laying a strong foundation for your mathematical journey. Understanding fractions isn't just about solving problems; it's about developing crucial problem-solving skills applicable across various aspects of life. So embrace the challenge, practice regularly, and watch your mathematical abilities soar!
Latest Posts
Latest Posts
-
What Height Is 54 Inches
Sep 21, 2025
-
Punctuation For A Movie Title
Sep 21, 2025
-
The Last Unicorn Book Summary
Sep 21, 2025
-
How Many Oz In 1 75l
Sep 21, 2025
-
Who Is Tiresias In Antigone
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Divide 1 3 By 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.