Differentiate X 1 X 1
scising
Sep 06, 2025 · 5 min read
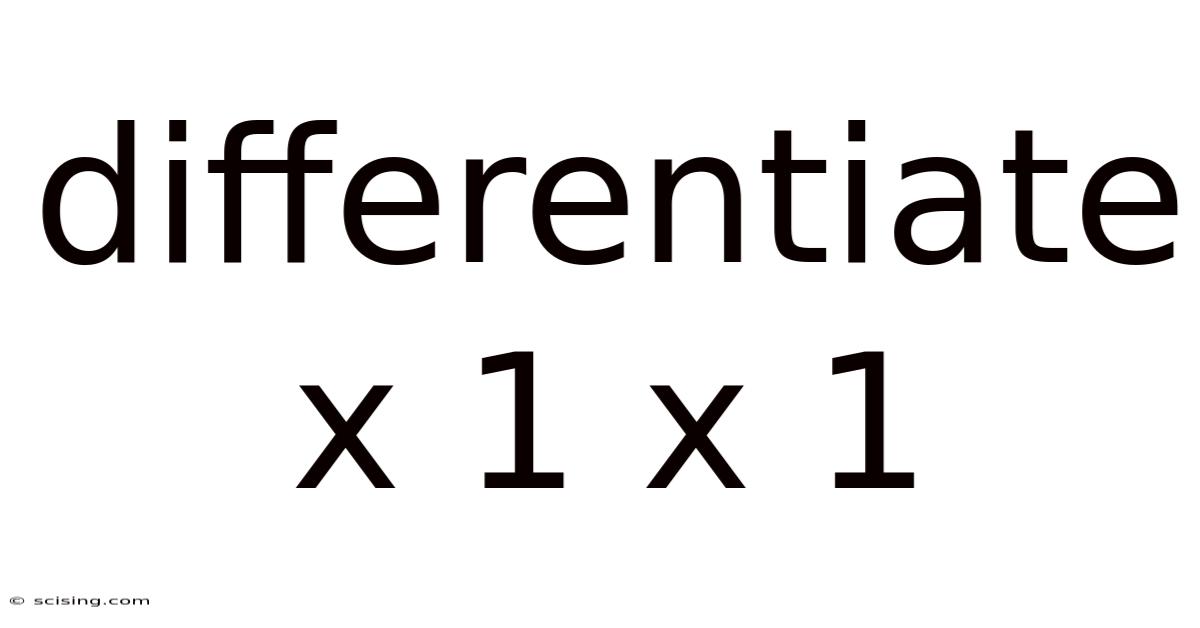
Table of Contents
Differentiate x¹ x¹: A Deep Dive into Calculus and its Applications
Understanding differentiation, a cornerstone of calculus, is crucial for numerous fields, from physics and engineering to economics and finance. This article will delve into the differentiation of the expression x¹ x¹, clarifying the process and exploring its broader implications. While the expression itself is deceptively simple, understanding its differentiation lays the groundwork for tackling more complex functions. We'll explore the fundamental rules of differentiation, practical applications, and address common questions.
Introduction: Unveiling the Power of Differentiation
Differentiation, in its simplest form, allows us to find the instantaneous rate of change of a function. Imagine you're tracking the speed of a car. While the speedometer gives you an average speed over a short period, differentiation provides the exact speed at any given instant. This instantaneous rate of change is represented by the derivative of the function. For the expression x¹ x¹, which simplifies to x², we will explore how to determine its derivative.
Step-by-Step Differentiation of x²
The fundamental rule we'll utilize is the power rule of differentiation. The power rule states that the derivative of xⁿ is nxⁿ⁻¹, where 'n' is any real number. Let's apply this to x²:
-
Identify the power: In x², the power (n) is 2.
-
Apply the power rule: The derivative is obtained by multiplying the coefficient (which is 1 in this case) by the power and then reducing the power by 1.
-
Calculation: The derivative of x² is (1 * 2)x⁽²⁻¹⁾ = 2x¹. This simplifies to 2x.
Therefore, the derivative of x¹ x¹ (which is x²) is 2x. This signifies that the instantaneous rate of change of the function x² at any given point 'x' is twice the value of 'x'.
Visualizing the Derivative: A Geometric Interpretation
The derivative of a function at a specific point represents the slope of the tangent line to the graph of the function at that point. If we were to graph y = x², we would see a parabola. The derivative, 2x, gives us the slope of the tangent line at any point on this parabola. For example:
- At x = 1, the slope of the tangent is 2(1) = 2.
- At x = 2, the slope of the tangent is 2(2) = 4.
- At x = 0, the slope of the tangent is 2(0) = 0.
This geometric interpretation provides a powerful visual understanding of what the derivative represents. The steeper the curve, the greater the magnitude of the derivative.
Beyond the Basics: Extending the Concept
While we've focused on x², the principles extend to more complex functions. Let's consider some examples to illustrate the versatility of differentiation:
-
Polynomials: Differentiation is straightforward for polynomials. For example, the derivative of 3x³ + 2x² + x + 5 is 9x² + 4x + 1. We apply the power rule to each term individually.
-
Products of Functions: When differentiating the product of two functions, we use the product rule: d/dx [f(x)g(x)] = f'(x)g(x) + f(x)g'(x). For instance, if we had x¹ multiplied by another function like 2x, applying the product rule helps find the derivative.
-
Quotients of Functions: The quotient rule is used for functions in the form f(x)/g(x): d/dx [f(x)/g(x)] = [f'(x)g(x) - f(x)g'(x)] / [g(x)]².
-
Chain Rule: The chain rule addresses composite functions, functions within functions. The derivative of a composite function, f(g(x)), is f'(g(x)) * g'(x).
Mastering these rules empowers you to differentiate a wide range of functions, forming the foundation for solving more complex problems in calculus and its applications.
Practical Applications: Where Differentiation Makes a Difference
The applications of differentiation are vast and far-reaching:
-
Physics: Calculating velocity and acceleration from displacement functions, understanding the rate of change of energy, and analyzing forces.
-
Engineering: Designing optimal structures, predicting the stress and strain on materials, and controlling systems based on dynamic behavior.
-
Economics: Determining marginal cost, marginal revenue, and maximizing profit in economic models.
-
Machine Learning: Optimizing algorithms by finding the minimum or maximum of a function through gradient descent methods, a process heavily reliant on derivatives.
-
Medicine: Modeling the spread of diseases, analyzing physiological data, and optimizing drug delivery systems.
Frequently Asked Questions (FAQ)
Q: What is the difference between a derivative and an integral?
A: Differentiation and integration are inverse operations. Differentiation finds the instantaneous rate of change of a function, while integration finds the area under the curve of a function. They are fundamental concepts in calculus.
Q: Can I differentiate any function?
A: Most continuous functions are differentiable, but there are exceptions. Functions with sharp corners or discontinuities are not differentiable at those points.
Q: Why is differentiation important?
A: Differentiation provides a powerful tool to analyze the behavior of functions, enabling us to understand rates of change, optimization, and modeling dynamic systems across many fields.
Q: What are higher-order derivatives?
A: Higher-order derivatives are obtained by differentiating a function multiple times. The second derivative represents the rate of change of the first derivative (e.g., acceleration is the second derivative of displacement).
Q: How do I apply differentiation to real-world problems?
A: The application depends on the specific problem. You need to create a mathematical model that represents the system, express it as a function, and then use differentiation to analyze its rate of change or optimization.
Conclusion: A Foundation for Further Exploration
The differentiation of x¹ x¹ (or x²) is a seemingly simple yet crucial concept in calculus. Understanding its derivation, both algebraically and geometrically, lays a solid foundation for tackling more complex functions and their applications. Mastering differentiation empowers you to analyze rates of change, optimize systems, and model dynamic processes across a wide range of disciplines. This is not merely an academic exercise; it's a key skill with significant practical relevance in the modern world. Further exploration into the rules of differentiation, along with practice and application, will solidify your understanding and unlock the full potential of this powerful mathematical tool. The journey into calculus is a rewarding one, filled with intellectual challenges and real-world applications that continue to expand as you delve deeper into the subject.
Latest Posts
Latest Posts
-
Q Hora Es En Pensilvania
Sep 06, 2025
-
How Tall Is 62 Centimeters
Sep 06, 2025
-
Study Com Wgu Computer Science
Sep 06, 2025
-
What Is A Sensory Language
Sep 06, 2025
-
Symbolism Of The Great Gatsby
Sep 06, 2025
Related Post
Thank you for visiting our website which covers about Differentiate X 1 X 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.