8 7/8 As A Decimal
scising
Sep 19, 2025 · 5 min read
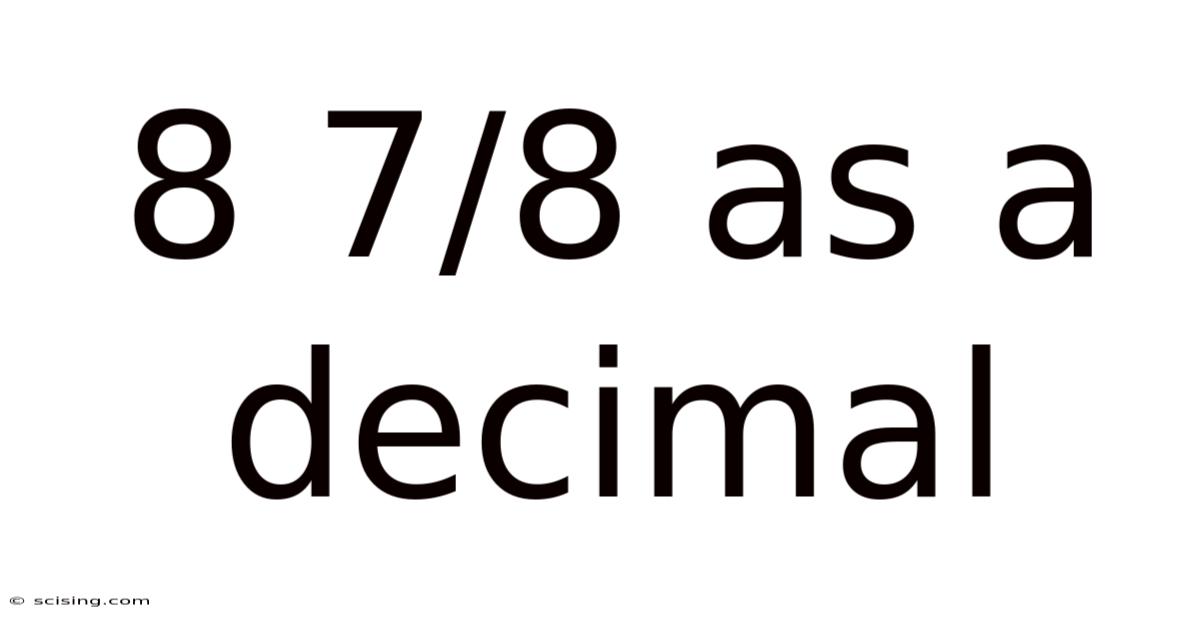
Table of Contents
8 7/8 as a Decimal: A Comprehensive Guide
Converting fractions to decimals is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced scientific computations. This comprehensive guide will delve into the process of converting the mixed number 8 7/8 into its decimal equivalent, exploring the underlying principles and providing practical examples. We'll cover different methods, address potential challenges, and even touch upon the significance of this conversion in various fields. Understanding this seemingly simple conversion opens doors to a deeper appreciation of numerical representation and its practical uses.
Understanding Mixed Numbers and Fractions
Before we embark on the conversion of 8 7/8 to a decimal, let's briefly review the concepts of mixed numbers and fractions. A mixed number combines a whole number and a fraction, such as 8 7/8. The whole number represents the complete units, while the fraction indicates a portion of a whole unit. In our example, 8 7/8 signifies eight complete units and seven-eighths of another unit.
A fraction, on the other hand, expresses a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator represents the number of parts we have, while the denominator represents the total number of parts that make up a whole. In the fraction 7/8, 7 is the numerator and 8 is the denominator.
Method 1: Converting the Fraction to a Decimal, then Adding the Whole Number
This is perhaps the most straightforward method. We first convert the fractional part (7/8) into a decimal and then add the whole number (8).
To convert 7/8 to a decimal, we perform a simple division: 7 divided by 8. This can be done using long division, a calculator, or even some mental math techniques if you're familiar with common fractions.
7 ÷ 8 = 0.875
Now, we add the whole number:
8 + 0.875 = 8.875
Therefore, 8 7/8 as a decimal is 8.875.
Method 2: Converting the Mixed Number Directly to an Improper Fraction, then to a Decimal
This method involves transforming the mixed number into an improper fraction first, and then converting the improper fraction to a decimal. An improper fraction has a numerator that is greater than or equal to its denominator.
To convert 8 7/8 into an improper fraction, we follow these steps:
- Multiply the whole number by the denominator: 8 * 8 = 64
- Add the numerator to the result: 64 + 7 = 71
- Keep the same denominator: The denominator remains 8.
So, 8 7/8 as an improper fraction is 71/8.
Now, we convert 71/8 to a decimal by performing the division:
71 ÷ 8 = 8.875
Again, we arrive at the same decimal equivalent: 8.875.
Method 3: Using Decimal Equivalents of Common Fractions
This method leverages the knowledge of common decimal equivalents of fractions. If you memorize some common fractions and their decimal counterparts, you can speed up the conversion process. For example, knowing that 1/8 = 0.125, you can quickly calculate 7/8:
7/8 = 7 * (1/8) = 7 * 0.125 = 0.875
Then, as before, add the whole number:
8 + 0.875 = 8.875
Understanding the Decimal Representation: Place Value
The decimal representation 8.875 signifies:
- 8: This is the whole number part, representing eight complete units.
- 8: This digit is in the tenths place (1/10), representing 8/10.
- 7: This digit is in the hundredths place (1/100), representing 7/100.
- 5: This digit is in the thousandths place (1/1000), representing 5/1000.
Therefore, 8.875 can be expressed as 8 + 8/10 + 7/100 + 5/1000.
Practical Applications of Decimal Conversion
Converting fractions to decimals is essential in many practical applications:
- Financial Calculations: Dealing with money often involves decimal values. Converting fractional parts of currency (like cents) to decimals ensures accurate calculations.
- Measurement and Engineering: Precise measurements in engineering and other scientific fields require decimal notation for accuracy and consistency.
- Data Analysis and Statistics: Statistical computations often involve working with decimal numbers for representing averages, proportions, and other statistical measures.
- Computer Programming: Computers typically store and manipulate numbers in decimal format, making the conversion essential for programming applications.
Common Mistakes to Avoid
- Incorrect Division: Ensure you perform the division correctly when converting the fraction to a decimal. Double-check your calculations to avoid errors.
- Forgetting the Whole Number: Don't forget to add the whole number back to the decimal representation of the fractional part.
- Incorrect Placement of the Decimal Point: Pay close attention to the placement of the decimal point when writing the final decimal value.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to convert 8 7/8 to a decimal?
A: Yes, absolutely! Most calculators have the functionality to perform division directly, making the conversion simple and efficient.
Q: Why is it important to learn different methods for converting fractions to decimals?
A: Understanding multiple methods helps you develop a deeper understanding of the underlying mathematical concepts. It also allows you to choose the most efficient method depending on the specific problem.
Q: What if the fraction doesn't divide evenly, resulting in a repeating decimal?
A: Some fractions result in non-terminating, repeating decimals (e.g., 1/3 = 0.333...). In such cases, you might round the decimal to a specific number of decimal places for practical purposes.
Q: Are there online tools available for fraction-to-decimal conversion?
A: Yes, many online calculators and converters are readily available to assist with this type of conversion.
Conclusion
Converting the mixed number 8 7/8 to its decimal equivalent (8.875) is a straightforward process that involves either directly converting the fraction to a decimal and adding the whole number, or converting the entire mixed number to an improper fraction and then to a decimal. Understanding this conversion is crucial for various applications, and mastering the different methods equips you with valuable mathematical skills applicable in many areas of life, from everyday calculations to complex scientific and engineering problems. The seemingly simple task of converting 8 7/8 to a decimal reveals the fundamental principles of numerical representation and the power of mathematical proficiency. By understanding the process, you build a strong foundation for more advanced mathematical concepts.
Latest Posts
Latest Posts
-
Ghost Of Christmas Past Costume
Sep 19, 2025
-
How Long Is 70 Cm
Sep 19, 2025
-
Words That Rhyme With Short
Sep 19, 2025
-
Is Nad To Nadh Exergonic
Sep 19, 2025
-
What Is A Natural Right
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 8 7/8 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.