7 1/2 As A Decimal
scising
Sep 11, 2025 · 6 min read
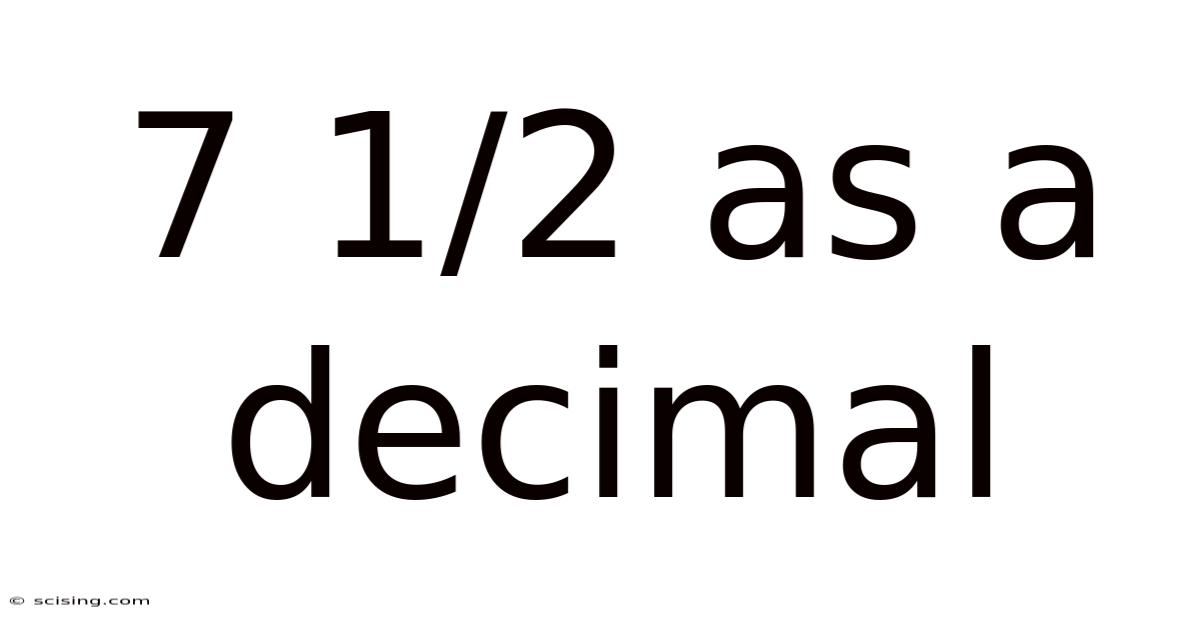
Table of Contents
7 1/2 as a Decimal: A Comprehensive Guide
Understanding how to convert fractions to decimals is a fundamental skill in mathematics. This comprehensive guide will explore the conversion of the mixed number 7 1/2 into its decimal equivalent, providing a step-by-step explanation, exploring the underlying mathematical principles, and answering frequently asked questions. This will equip you with a solid understanding not just of this specific conversion, but of fractional-to-decimal conversions in general.
Introduction: Understanding Mixed Numbers and Decimals
Before diving into the conversion of 7 1/2, let's clarify some basic concepts. A mixed number combines a whole number and a fraction, such as 7 1/2. A decimal, on the other hand, represents a number using a base-ten system, with a decimal point separating the whole number part from the fractional part. For example, 7.5 is a decimal. Converting a mixed number to a decimal involves expressing the fractional part as a decimal and then combining it with the whole number part.
Step-by-Step Conversion of 7 1/2 to a Decimal
The conversion of 7 1/2 to a decimal is straightforward. Here's a step-by-step approach:
-
Separate the whole number and the fraction: The mixed number 7 1/2 consists of a whole number part (7) and a fractional part (1/2).
-
Convert the fraction to a decimal: To convert the fraction 1/2 to a decimal, you divide the numerator (1) by the denominator (2): 1 ÷ 2 = 0.5.
-
Combine the whole number and the decimal: Now, combine the whole number (7) with the decimal equivalent of the fraction (0.5) to get the final decimal representation: 7.5.
Therefore, 7 1/2 as a decimal is 7.5.
Different Methods for Converting Fractions to Decimals
While the method above is the most intuitive for 7 1/2, let's explore other methods applicable to various fractions:
-
Direct Division: This is the most fundamental method. For any fraction a/b, you simply divide a by b. This method works for all fractions, regardless of whether the denominator is a power of 10.
-
Converting to a Denominator of 10, 100, 1000, etc.: If the denominator of the fraction can be easily converted to a power of 10 (10, 100, 1000, and so on) by multiplying both the numerator and the denominator by the same number, this method provides a quick route to the decimal equivalent. For example, to convert 3/5 to a decimal, we multiply both the numerator and denominator by 2 to get 6/10, which is equivalent to 0.6. This method isn't always possible (e.g., 1/3 cannot be easily converted to a denominator that is a power of 10).
-
Using a Calculator: A calculator provides the quickest way to convert any fraction to its decimal equivalent. Simply enter the fraction as a division problem (numerator divided by denominator) and the calculator will display the decimal value.
Understanding the Mathematical Principles Behind the Conversion
The conversion from a fraction to a decimal hinges on the fundamental relationship between fractions and division. A fraction, like a/b, represents the division of a by b. Therefore, converting a fraction to a decimal is simply performing this division. The decimal point separates the whole number part from the fractional part, representing values less than one.
In the case of 7 1/2, we have 7 whole units plus 1/2 of a unit. Dividing 1 by 2 gives us 0.5, representing half a unit. Adding this to the 7 whole units results in 7.5.
Illustrative Examples: Converting Other Mixed Numbers to Decimals
Let's apply the learned methods to convert a few more mixed numbers into decimals:
-
3 1/4: The fraction 1/4 is equivalent to 1 ÷ 4 = 0.25. Therefore, 3 1/4 as a decimal is 3.25.
-
5 2/5: The fraction 2/5 can be converted to a denominator of 10 by multiplying both the numerator and denominator by 2, giving us 4/10 = 0.4. Therefore, 5 2/5 as a decimal is 5.4.
-
12 3/8: Dividing 3 by 8, we get 0.375. Thus, 12 3/8 as a decimal is 12.375.
-
2 1/3: Dividing 1 by 3 gives us a repeating decimal: 0.3333... This is often written as 0.3̅. Therefore, 2 1/3 as a decimal is 2.3̅.
Working with Repeating Decimals
Some fractions, when converted to decimals, result in repeating decimals. These decimals have a sequence of digits that repeat infinitely. For example, 1/3 = 0.3333... These are often represented with a bar over the repeating sequence (e.g., 0.3̅). Understanding repeating decimals is crucial for accurate calculations involving fractions. While calculators may truncate repeating decimals, it's important to recognize their true nature.
Real-World Applications of Decimal Conversions
The ability to convert fractions to decimals is essential in numerous real-world scenarios:
-
Financial Calculations: Calculating percentages, interest rates, and discounts often involve converting fractions to decimals.
-
Measurement: Many measurements involve fractions, but converting them to decimals is often more convenient for calculations. For instance, converting fractional inches to decimal inches for precision engineering.
-
Data Analysis: Representing data in decimal form simplifies many statistical calculations and analyses.
-
Scientific Calculations: In science and engineering, precise measurements and calculations often require decimal representations.
Frequently Asked Questions (FAQ)
Q1: Why is it important to learn how to convert fractions to decimals?
A1: Converting fractions to decimals is a crucial skill in mathematics and has widespread applications in various fields, including finance, science, engineering, and everyday life. It allows for easier computations and comparison of quantities.
Q2: What if the fraction has a large denominator? How do I convert it to a decimal?
A2: Even with large denominators, the method remains the same: divide the numerator by the denominator. You can use a calculator for this, especially for complex fractions.
Q3: Can all fractions be converted to terminating decimals (decimals that end)?
A3: No, not all fractions can be converted to terminating decimals. Fractions with denominators that have prime factors other than 2 and 5 will result in repeating decimals.
Q4: How do I deal with repeating decimals in calculations?
A4: In many calculations, you can round repeating decimals to a sufficient number of decimal places for practical purposes. However, it is important to understand that the rounding introduces a small error. For exact calculations, it is often better to work with the fraction itself.
Q5: What is the difference between a mixed number and an improper fraction?
A5: A mixed number combines a whole number and a fraction (e.g., 7 1/2). An improper fraction has a numerator that is greater than or equal to the denominator (e.g., 15/2). Both represent the same quantity, but have different forms. To convert a mixed number to a decimal, it's often easier to first convert it to an improper fraction (in this case, 15/2) and then perform the division.
Conclusion: Mastering Fraction-to-Decimal Conversions
Converting fractions, including mixed numbers, to decimals is a fundamental mathematical skill. Understanding the different methods, the underlying principles, and the potential for repeating decimals is crucial. This skill simplifies calculations and expands your ability to work with numbers in various contexts. The step-by-step approach outlined in this guide, along with the illustrative examples and FAQs, should provide a solid foundation for mastering this essential mathematical concept. Practice is key – the more you practice, the more comfortable and proficient you will become. So, grab a pencil, paper, and some fractions, and start practicing your conversions!
Latest Posts
Latest Posts
-
Map Of The River Seine
Sep 11, 2025
-
Examples Of Density Dependant Factors
Sep 11, 2025
-
How Long Is 12 Cm
Sep 11, 2025
-
How To Graph A Line
Sep 11, 2025
-
Isoelectric Point Of Amino Acids
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 7 1/2 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.