60 Percent In Decimal Form
scising
Sep 21, 2025 · 5 min read
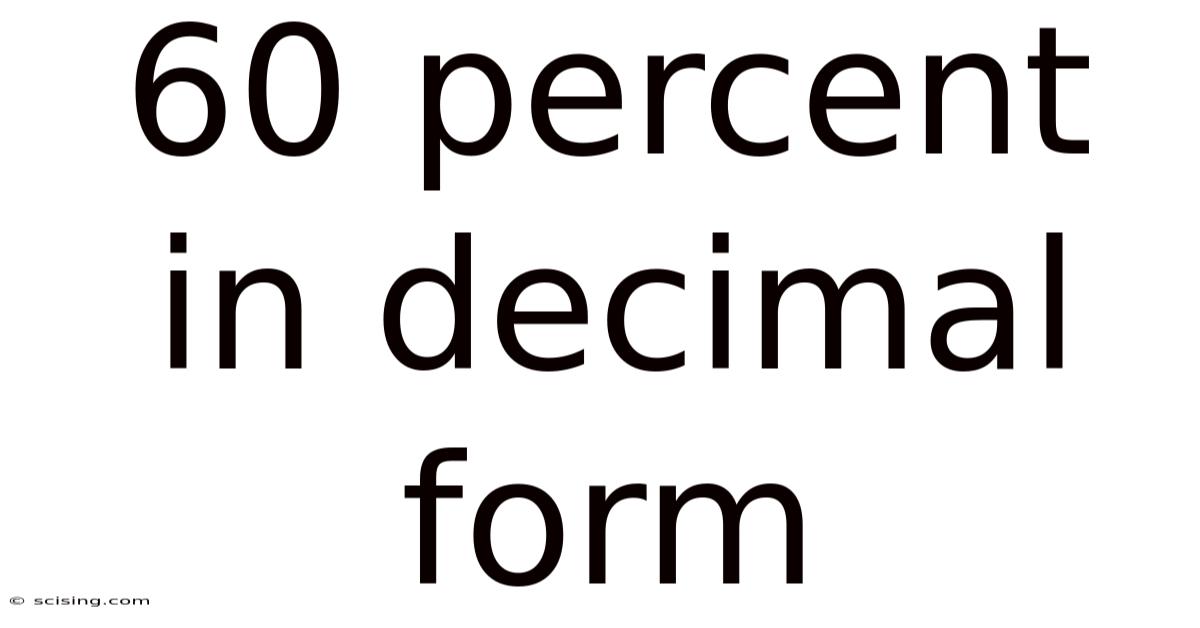
Table of Contents
60 Percent in Decimal Form: A Comprehensive Guide
Understanding percentages and their decimal equivalents is a fundamental skill in mathematics and has widespread applications in various fields, from finance and statistics to everyday calculations. This article will delve deep into understanding how to convert 60 percent to its decimal form, explain the underlying principles, and explore practical applications. We'll also tackle common misconceptions and answer frequently asked questions, ensuring a comprehensive understanding of this crucial concept.
Introduction: Percentages and Decimals
A percentage represents a fraction of 100. The word "percent" literally means "per hundred." So, 60% means 60 out of 100, or 60/100. A decimal is a number expressed in the base-10 system, using a decimal point to separate the whole number part from the fractional part. Converting between percentages and decimals is a straightforward process, crucial for calculations involving proportions, ratios, and more.
Converting 60% to Decimal Form: The Step-by-Step Process
The conversion of 60% to its decimal equivalent is relatively simple. Here's a step-by-step breakdown:
-
Understanding the Meaning: Remember that 60% means 60 parts out of 100. This can be written as the fraction 60/100.
-
Dividing the Numerator by the Denominator: To convert the fraction to a decimal, we divide the numerator (60) by the denominator (100). This gives us: 60 ÷ 100 = 0.6
-
The Decimal Equivalent: Therefore, 60% in decimal form is 0.6.
This process can be generalized for any percentage. To convert a percentage to a decimal, simply divide the percentage by 100.
The Underlying Mathematical Principle: Fractions, Decimals, and Percentages
The relationship between fractions, decimals, and percentages is fundamental to understanding this conversion. They are all different ways of representing the same proportion or part of a whole.
-
Fraction: A fraction represents a part of a whole, expressed as a ratio of two numbers (numerator/denominator). For example, 60% is represented as the fraction 60/100.
-
Decimal: A decimal represents a part of a whole using the base-10 number system. The decimal point separates the whole number from the fractional part. For example, 0.6 represents six-tenths.
-
Percentage: A percentage represents a part of a whole as a fraction of 100. The "%" symbol denotes this relationship.
The conversion between these three forms involves understanding these relationships and applying basic arithmetic operations like division and multiplication.
Practical Applications of 60% in Decimal Form (0.6)
The decimal equivalent of 60%, 0.6, finds extensive use in various real-world scenarios:
-
Finance: Calculating interest rates, discounts, profit margins, and tax rates often involves converting percentages to decimals. For instance, calculating a 60% discount on an item would involve multiplying the item's price by 0.6.
-
Statistics: Many statistical calculations require working with proportions and probabilities, often expressed as percentages. Converting to decimals simplifies these calculations.
-
Science: Scientific data often involves representing proportions and ratios, frequently expressed as percentages which are then converted to decimals for calculations and analysis.
-
Everyday Life: Calculating tips, sales tax, or determining percentages of ingredients in recipes all benefit from understanding the decimal representation of percentages.
Common Misconceptions and How to Avoid Them
While the conversion process is straightforward, some common misconceptions can lead to errors:
-
Misplacing the Decimal Point: A frequent error is incorrectly placing the decimal point when converting a percentage to a decimal. Remember to always divide by 100, which essentially moves the decimal point two places to the left.
-
Confusing Percentages with Decimals Directly: While 60% is equal to 0.6, it's crucial to understand the underlying process of division by 100 rather than simply memorizing a few conversions.
-
Incorrect Calculation with Decimal Equivalents: When using the decimal equivalent in calculations (like calculating discounts), ensure the correct mathematical operation is applied (multiplication, addition, subtraction, or division, as appropriate).
Advanced Applications: Working with 60% in Complex Calculations
While the basic conversion is simple, understanding how 0.6 interacts in more complex calculations is crucial. For example:
-
Compound Interest: Calculating compound interest involves repeated multiplication using the decimal equivalent of the interest rate.
-
Probability and Statistics: In probability calculations, the decimal representation of percentages simplifies the calculation of probabilities and expected values.
-
Regression Analysis: In statistical modeling (like linear regression), coefficients are often expressed as decimals representing the impact of one variable on another, where the percentage change might be the underlying context.
Frequently Asked Questions (FAQs)
-
Q: How do I convert a decimal back to a percentage?
- A: To convert a decimal back to a percentage, simply multiply the decimal by 100 and add the "%" symbol. For example, 0.6 x 100 = 60%,
-
Q: What if the percentage is less than 1%?
- A: For percentages less than 1%, the decimal equivalent will have a leading zero before the digits. For example, 0.5% is 0.005 in decimal form.
-
Q: Can I use a calculator to convert percentages to decimals?
- A: Yes, most calculators have a percentage function that simplifies this conversion. Alternatively, you can manually divide the percentage by 100.
-
Q: Why is understanding this conversion important?
- A: Understanding this conversion is crucial for accurate calculations in many fields, including finance, statistics, science, and everyday life. It allows for smoother transitions between different ways of expressing proportions and ratios.
Conclusion: Mastering the Conversion of 60% to 0.6
Converting 60% to its decimal form, 0.6, is a fundamental mathematical skill with broad applications. This article provided a detailed explanation of the conversion process, the underlying mathematical principles, and various practical applications. By understanding the relationship between fractions, decimals, and percentages, you can confidently handle calculations involving percentages in diverse contexts, improving your skills in mathematics and related fields. Remember to practice regularly to build confidence and mastery of this essential skill. Understanding this conversion empowers you to confidently tackle numerical challenges in various aspects of your life and work.
Latest Posts
Latest Posts
-
Characteristics Of Traditional Economic System
Sep 21, 2025
-
Economy For New England Colonies
Sep 21, 2025
-
Squealer Quotes From Animal Farm
Sep 21, 2025
-
Rational Numbers On Coordinate Plane
Sep 21, 2025
-
12 Inches In A Foot
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 60 Percent In Decimal Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.