6 Times What Equals 100
scising
Sep 21, 2025 · 5 min read
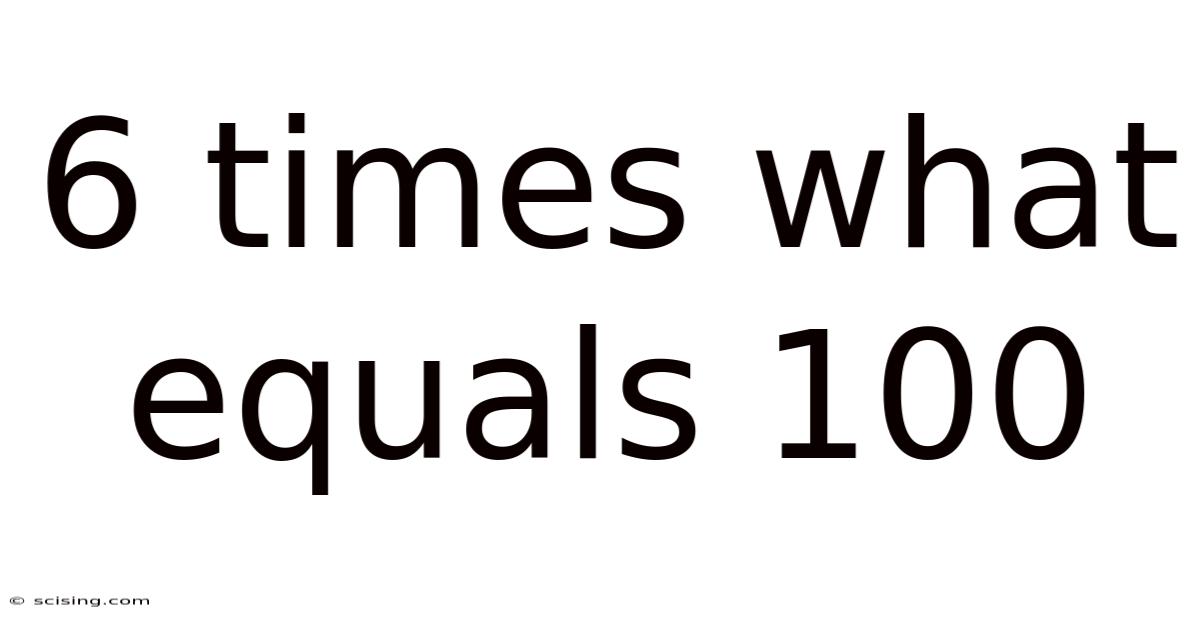
Table of Contents
Decoding the Mystery: 6 Times What Equals 100? A Deep Dive into Division and its Applications
This article explores the seemingly simple question, "6 times what equals 100?" It goes beyond the straightforward answer to delve into the underlying mathematical principles, explore different methods for solving similar problems, and demonstrate the practical applications of division in various fields. Understanding this concept is crucial for building a strong foundation in mathematics and problem-solving skills. We'll uncover the solution, examine the process, and discuss its relevance in everyday life and specialized fields.
Understanding the Problem: 6x = 100
The core of the problem lies in understanding the relationship between multiplication and division. The equation "6 times what equals 100" can be mathematically represented as:
6x = 100
Where 'x' represents the unknown number we're trying to find. This equation signifies that six times an unknown value ('x') results in a product of 100. To solve for 'x', we need to use the inverse operation of multiplication, which is division.
Solving the Equation: Unveiling the Answer
To find the value of 'x', we divide both sides of the equation by 6:
6x / 6 = 100 / 6
This simplifies to:
x = 16.666...
Therefore, the answer to "6 times what equals 100?" is approximately 16.67. It's important to note that this is a recurring decimal, meaning the digits "6" repeat infinitely. For practical purposes, rounding to two decimal places is often sufficient.
Different Methods for Solving Division Problems
While the above method is the most straightforward, several other approaches can be used to solve division problems like this:
-
Long Division: This traditional method involves a step-by-step process of dividing the dividend (100) by the divisor (6). This method is excellent for understanding the underlying mechanics of division and is particularly useful when dealing with larger numbers.
-
Short Division: A shorter version of long division, suitable for simpler problems. It's a quicker method but may require a stronger understanding of multiplication tables.
-
Calculator: For quick solutions, a calculator provides the most efficient method. Simply input "100 ÷ 6" to obtain the answer.
-
Fractions: The problem can also be expressed as a fraction: 100/6. This fraction can then be simplified to its lowest terms (50/3) and converted into a decimal by dividing the numerator by the denominator.
Practical Applications of Division: Beyond the Classroom
Division isn't just a mathematical concept confined to textbooks; it's a fundamental operation with widespread practical applications across various fields:
-
Everyday Finances: Dividing your monthly income by the number of weeks in a month helps calculate your weekly budget. Similarly, you can use division to determine the cost per unit when buying items in bulk.
-
Cooking and Baking: Following recipes often requires dividing ingredients proportionally. For example, if a recipe calls for a certain quantity of ingredients for a specific number of servings, you’d need to divide to scale the recipe up or down.
-
Engineering and Construction: Engineers frequently use division in calculations related to material requirements, load distribution, and structural design. Accurate division ensures that structures are stable and efficient.
-
Data Analysis and Statistics: Division plays a critical role in calculating averages, ratios, and percentages, which are essential in various statistical analyses. These analyses are crucial for understanding trends and making informed decisions in fields like business, science, and social sciences.
-
Science and Research: From calculating reaction rates in chemistry to analyzing experimental data in physics, division is an indispensable tool in many scientific fields.
-
Computer Science: Division is a fundamental arithmetic operation within computer programming, employed in a vast range of algorithms and computational tasks.
-
Geography and Cartography: Calculating distances, scales, and areas on maps relies heavily on division. Map projections and geographic information systems (GIS) utilize division extensively for data processing and analysis.
Exploring the Concept Further: Beyond the Simple Answer
The solution to "6 times what equals 100" is more than just a numerical answer; it's a gateway to understanding broader mathematical concepts. Let's explore some related topics:
-
Remainders: When dividing, we don't always get a whole number. In the case of 100/6, there's a remainder. Understanding remainders is crucial for various applications, from scheduling to inventory management.
-
Decimal Representation: The solution (16.666...) highlights the importance of decimal numbers and their representation. Understanding decimal places and rounding is vital for practical applications where exact values may not be necessary.
-
Proportionality: The problem illustrates the concept of proportionality. The unknown number ('x') is directly proportional to 100 and inversely proportional to 6.
-
Inverse Operations: Solving the equation demonstrates the relationship between multiplication and division as inverse operations. This understanding is fundamental for solving a wide array of algebraic equations.
Frequently Asked Questions (FAQ)
Q: What if the problem was "6 times what equals 101"?
A: The approach remains the same. Divide 101 by 6 to find the answer (approximately 16.83).
Q: Can this problem be solved without using division?
A: While less direct, you could use trial and error, progressively multiplying 6 by different numbers until you get close to 100. This method is less efficient, especially for more complex problems.
Q: What are some real-world scenarios where I might encounter this type of problem?
A: You might encounter this type of problem when splitting a cost equally among a group of people, distributing resources proportionally, or scaling recipes in cooking.
Q: How can I improve my understanding of division?
A: Practice regularly using different methods, work through problems with varying degrees of difficulty, and consider exploring online resources or seeking tutoring if needed.
Conclusion: Mastering Division and its Applications
The simple question, "6 times what equals 100?", unlocks a wealth of mathematical concepts and practical applications. Understanding division, its different methods, and its widespread use across various fields is crucial for developing strong problem-solving skills and navigating numerous real-world scenarios. By mastering this fundamental operation, you'll build a solid foundation for tackling more complex mathematical challenges and making informed decisions in all aspects of life. Remember, the journey of learning is ongoing, so keep exploring, keep practicing, and keep discovering the power of mathematics!
Latest Posts
Latest Posts
-
Economy For New England Colonies
Sep 21, 2025
-
Squealer Quotes From Animal Farm
Sep 21, 2025
-
Rational Numbers On Coordinate Plane
Sep 21, 2025
-
12 Inches In A Foot
Sep 21, 2025
-
Lord Of The Flies Conflict
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 6 Times What Equals 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.