5y 1 6x 4y 10
scising
Sep 17, 2025 · 6 min read
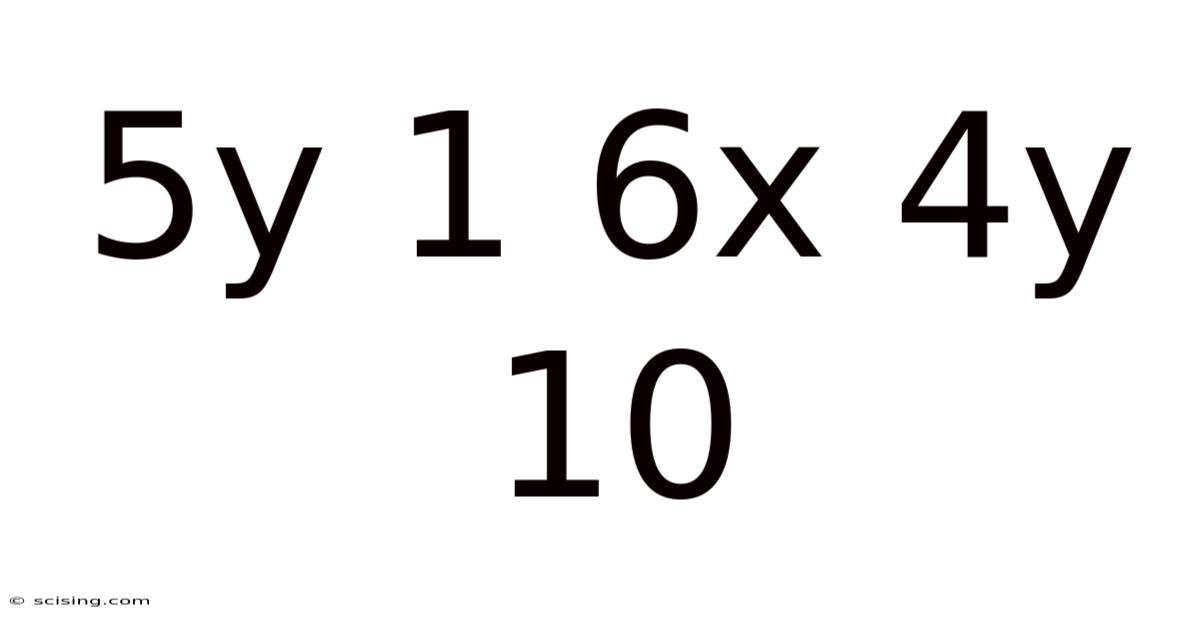
Table of Contents
Decoding 5y + 1 = 6x + 4y + 10: A Deep Dive into Linear Equations and Problem Solving
This article explores the linear equation 5y + 1 = 6x + 4y + 10, demonstrating how to solve it, its underlying mathematical principles, and its applications in various fields. We'll delve into the process step-by-step, clarifying each stage and highlighting the significance of understanding such equations. This seemingly simple equation provides a rich opportunity to understand core concepts in algebra and problem-solving strategies.
Introduction: Understanding Linear Equations
A linear equation is a mathematical statement that equates two expressions, where the highest power of the variables is 1. These equations are fundamental to algebra and are used extensively in various fields, including physics, engineering, economics, and computer science. They represent relationships between variables that can be graphed as straight lines. The equation 5y + 1 = 6x + 4y + 10 is a linear equation with two variables, x and y. Our goal is to find the values of x and y that satisfy this equation. This often involves finding a solution set, which represents all possible pairs of (x, y) values that make the equation true. In some cases, there might be an infinite number of solutions, a single solution, or no solution at all.
Step-by-Step Solution: Simplifying and Solving the Equation
The first step in solving 5y + 1 = 6x + 4y + 10 is to simplify the equation by combining like terms. We can rearrange the equation to isolate one variable in terms of the other. Let's start by moving all the terms containing 'y' to one side and the terms containing 'x' and constants to the other:
-
Subtract 4y from both sides: 5y - 4y + 1 = 6x + 4y - 4y + 10 This simplifies to y + 1 = 6x + 10
-
Subtract 1 from both sides: y + 1 - 1 = 6x + 10 - 1 This gives us y = 6x + 9
Now we have expressed y in terms of x. This equation represents a straight line. For every value of x, we can calculate a corresponding value of y. This means there are infinitely many solutions to this equation. We can represent this solution set graphically as a straight line on the Cartesian coordinate system.
Graphical Representation: Visualizing the Solution Set
The equation y = 6x + 9 is in slope-intercept form (y = mx + b), where 'm' is the slope (6 in this case) and 'b' is the y-intercept (9). The slope indicates the steepness of the line, and the y-intercept is the point where the line crosses the y-axis.
To graph this equation:
-
Plot the y-intercept: The line intersects the y-axis at the point (0, 9).
-
Use the slope to find another point: The slope of 6 means that for every 1 unit increase in x, y increases by 6 units. So, starting from (0, 9), we can move 1 unit to the right and 6 units up to find another point on the line, (1, 15).
-
Draw the line: Draw a straight line passing through the points (0, 9) and (1, 15). This line represents all the possible solutions (x, y) that satisfy the original equation 5y + 1 = 6x + 4y + 10.
Finding Specific Solutions: Examples
While there are infinitely many solutions, we can find specific solutions by substituting a value for either x or y and solving for the other variable.
-
Example 1: If x = 0: Substituting x = 0 into y = 6x + 9 gives y = 6(0) + 9 = 9. Therefore, (0, 9) is a solution.
-
Example 2: If y = 15: Substituting y = 15 into y = 6x + 9 gives 15 = 6x + 9. Subtracting 9 from both sides gives 6 = 6x, and dividing by 6 gives x = 1. Therefore, (1, 15) is a solution.
-
Example 3: If x = -1: Substituting x = -1 into y = 6x + 9 gives y = 6(-1) + 9 = 3. Therefore (-1, 3) is a solution.
The Significance of Slope and Intercept
The slope (m = 6) tells us the rate of change of y with respect to x. For every unit increase in x, y increases by 6 units. The y-intercept (b = 9) indicates the value of y when x is 0. These parameters are crucial in interpreting the relationship between the variables and making predictions. In real-world applications, the slope might represent a rate of growth, speed, or any other proportional relationship. The y-intercept might represent an initial value or a starting point.
Applications of Linear Equations: Real-World Examples
Linear equations have wide-ranging applications across various disciplines. Here are a few examples:
-
Physics: Calculating velocity (v = u + at), where v is final velocity, u is initial velocity, a is acceleration, and t is time.
-
Economics: Modeling supply and demand, where the price (y) is related to the quantity (x).
-
Engineering: Determining the relationship between stress and strain in materials.
-
Computer Science: Representing relationships between data points and creating algorithms.
-
Finance: Calculating simple interest (I = Prt), where I is interest, P is principal, r is rate, and t is time.
Solving Systems of Equations: Expanding the Scope
Often, we encounter situations requiring solving multiple linear equations simultaneously, known as systems of equations. These systems can have one solution, infinitely many solutions, or no solutions. Techniques like substitution, elimination, and graphing can be used to find the solution to these systems. Our equation, y = 6x + 9, could be part of a larger system, and solving that system would involve incorporating the other equation(s) and finding the point(s) of intersection (if any).
Frequently Asked Questions (FAQ)
-
Q: Is there only one solution to the equation 5y + 1 = 6x + 4y + 10? A: No, there are infinitely many solutions because the equation represents a straight line.
-
Q: How can I check if a solution is correct? A: Substitute the values of x and y into the original equation. If both sides are equal, the solution is correct.
-
Q: What if the equation was more complex? A: The same principles apply. Simplify the equation by combining like terms and isolating one variable. More complex equations might involve more steps but the core concepts remain the same.
-
Q: What are some other methods to solve linear equations? A: Besides the method used above, other techniques include the elimination method and graphical methods (plotting the line and identifying the x and y intercepts or finding the intersection point with another line if it's a system of equations).
Conclusion: Mastering Linear Equations – A Foundation for Further Learning
Understanding linear equations is crucial for success in mathematics and various other fields. This seemingly simple equation, 5y + 1 = 6x + 4y + 10, provides a valuable opportunity to practice essential algebraic manipulation and problem-solving skills. From simplifying the equation to graphing the solution set and exploring real-world applications, this comprehensive analysis showcases the significance of linear equations and their role as a building block for more advanced mathematical concepts. Mastering this foundational concept will empower you to tackle more complex problems and build a strong base for future learning in mathematics and related disciplines. The key takeaway is the understanding of the process, the ability to represent solutions graphically, and the capacity to interpret the meaning of slope and intercepts within the context of a real-world problem.
Latest Posts
Latest Posts
-
Talk With Me In Spanish
Sep 17, 2025
-
Free Ged Science Practice Test
Sep 17, 2025
-
What Does That Mean Spanish
Sep 17, 2025
-
How Many Inches Is 56
Sep 17, 2025
-
Food Webs In Tropical Rainforest
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 5y 1 6x 4y 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.