5 X 2 2 125
scising
Sep 15, 2025 · 5 min read
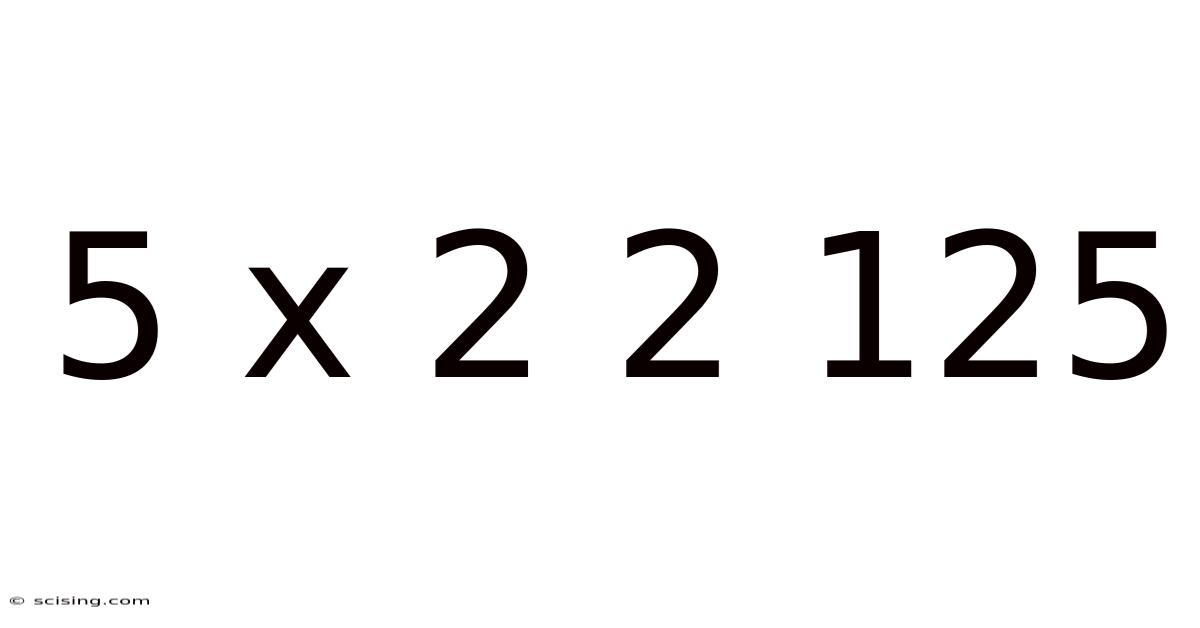
Table of Contents
Decoding the Enigma: Exploring the Mathematical Curiosity of 5 x 2 2 125
The seemingly simple sequence "5 x 2 2 125" might initially appear innocuous, even puzzling. However, a closer examination reveals a fascinating interplay between arithmetic, pattern recognition, and potentially, even deeper mathematical concepts. This article will delve into this numerical curiosity, exploring various interpretations, potential solutions, and the underlying principles that make it so intriguing. We'll dissect the problem, explore possible solutions, and discuss the broader mathematical concepts it touches upon. This exploration will be suitable for anyone with a basic understanding of arithmetic, making it an engaging journey even for those without advanced mathematical backgrounds.
Introduction: The Puzzle and its Ambiguity
The core of the puzzle lies in the inherent ambiguity of the expression "5 x 2 2 125". The lack of clear operational symbols (like +, -, ÷) between the numbers creates multiple potential interpretations. This inherent uncertainty is what makes this more than just a simple multiplication problem; it’s a challenge in logical reasoning and interpreting mathematical notation. We will systematically explore several plausible interpretations, analyzing each one for its validity and the mathematical principles involved.
Possible Interpretations and Solutions
Several interpretations of "5 x 2 2 125" are possible, depending on how we choose to infer the missing operators. Let's explore some of them:
1. Interpreting as a Single Multiplication:
One simplistic approach is to assume the expression implies a single, continuous multiplication: 5 * 2 * 2 * 125. This is a straightforward calculation:
5 * 2 = 10 10 * 2 = 20 20 * 125 = 2500
Therefore, under this interpretation, the answer is 2500. This is the most straightforward solution, relying on the basic principles of multiplication.
2. Incorporating Implicit Addition or Subtraction:
We could interpret the sequence as a combination of multiplication and addition/subtraction. However, without any explicit operators to guide us, this approach becomes highly speculative. Multiple combinations are possible, each yielding a different result. For instance:
- (5 x 2) + 2 + 125 = 10 + 2 + 125 = 137
- 5 x (2 + 2) + 125 = 5 x 4 + 125 = 20 + 125 = 145
- 5 x 2 x (2 + 125) = 10 x 127 = 1270
These examples demonstrate the high level of ambiguity. Without a clearer definition of how the numbers relate, it's impossible to definitively determine if any of these is the "correct" answer.
3. Exploring Base Systems:
A more advanced interpretation could involve considering different number bases. We typically use base-10 (decimal) system, but other bases, like binary (base-2) or hexadecimal (base-16), exist. However, without additional context or clues suggesting a non-decimal base, exploring this avenue becomes highly speculative and would lack solid mathematical grounding.
4. Considering a Pattern or Sequence:
Another approach is to look for a pattern or underlying mathematical sequence. While the initial numbers (5, 2, 2, 125) don't immediately reveal an obvious arithmetic or geometric progression, we can explore more complex relationships. This might involve investigating combinations of mathematical operations, looking for hidden links between the numbers. However, without more information or context, discovering a definitive pattern is unlikely.
Mathematical Principles at Play
Regardless of the chosen interpretation, the problem highlights several key mathematical principles:
-
Order of Operations (PEMDAS/BODMAS): The ambiguity of the expression underscores the importance of the order of operations (Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction). The lack of explicit operators necessitates assumptions about the order, leading to different results.
-
Mathematical Notation: This puzzle emphasizes the critical role of clear and unambiguous mathematical notation. The lack of operators illustrates how imprecise notation can lead to confusion and multiple interpretations.
-
Problem-Solving Strategies: This type of problem requires employing different problem-solving strategies. We need to consider various possible interpretations, analyze the implications of each, and evaluate their validity based on mathematical principles.
-
Ambiguity and Uncertainty: The problem directly confronts the concepts of ambiguity and uncertainty inherent in mathematics. It shows how, without sufficient constraints or clear definitions, a problem can have multiple valid solutions.
Expanding the Exploration: Related Mathematical Concepts
The "5 x 2 2 125" puzzle, though seemingly simple, can be a springboard for exploring more complex mathematical ideas:
-
Abstract Algebra: This branch of mathematics deals with abstract structures and operations, offering tools to analyze mathematical systems beyond basic arithmetic. The ambiguity of the original expression could be formally explored using abstract algebraic techniques, defining precise rules for interpreting similar expressions.
-
Formal Logic: Formal logic provides a framework for analyzing statements and inferences. The different interpretations of "5 x 2 2 125" can be formulated as logical expressions, allowing us to systematically evaluate the validity of each interpretation.
-
Number Theory: Number theory explores the properties of numbers. This could involve searching for patterns or relationships within the given numbers (5, 2, 2, 125) using number-theoretic techniques.
-
Computational Mathematics: Computational mathematics employs computational methods to solve mathematical problems. For complex expressions or sequences, computational methods might be used to explore potential solutions.
Frequently Asked Questions (FAQs)
Q: Is there one correct answer to 5 x 2 2 125?
A: No, without explicitly defined operators, there isn't a single "correct" answer. The ambiguity of the notation allows for multiple valid interpretations, each leading to a different result.
Q: How can I solve similar ambiguous mathematical expressions?
A: The key is to systematically consider different interpretations, guided by the principles of mathematical notation and order of operations. Start with the simplest interpretations and progressively explore more complex ones. If possible, seek additional context or information to clarify the intended meaning.
Q: What is the importance of clear mathematical notation?
A: Clear mathematical notation is crucial for avoiding ambiguity and ensuring accurate communication of mathematical ideas. Using standard symbols and conventions is essential to prevent misunderstandings and errors.
Conclusion: Beyond the Numbers
The seemingly simple expression "5 x 2 2 125" turns out to be a rich source of exploration. While it doesn't have a single definitive solution, its ambiguity highlights the crucial role of clear mathematical notation, order of operations, and the need for robust problem-solving strategies. This exploration demonstrates that even simple-looking mathematical puzzles can reveal deeper insights into mathematical principles and inspire exploration into more complex mathematical concepts. The challenge invites us to think critically about how we interpret mathematical expressions and highlights the beauty of mathematics in its ability to lead us to deeper understanding, even within apparent uncertainty. Its power lies not just in finding an answer, but in the process of exploring possibilities and uncovering the underlying principles that govern our mathematical world.
Latest Posts
Latest Posts
-
Spanish Adjectives Describing A Person
Sep 16, 2025
-
How To Create Hydrochloric Acid
Sep 16, 2025
-
Examples Of Absorption In Waves
Sep 16, 2025
-
Convert Mg To Oz Calculator
Sep 16, 2025
-
Gerrymandering Ap Human Geography Example
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 5 X 2 2 125 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.