5 Percent Of 1.5 Million
scising
Sep 25, 2025 · 6 min read
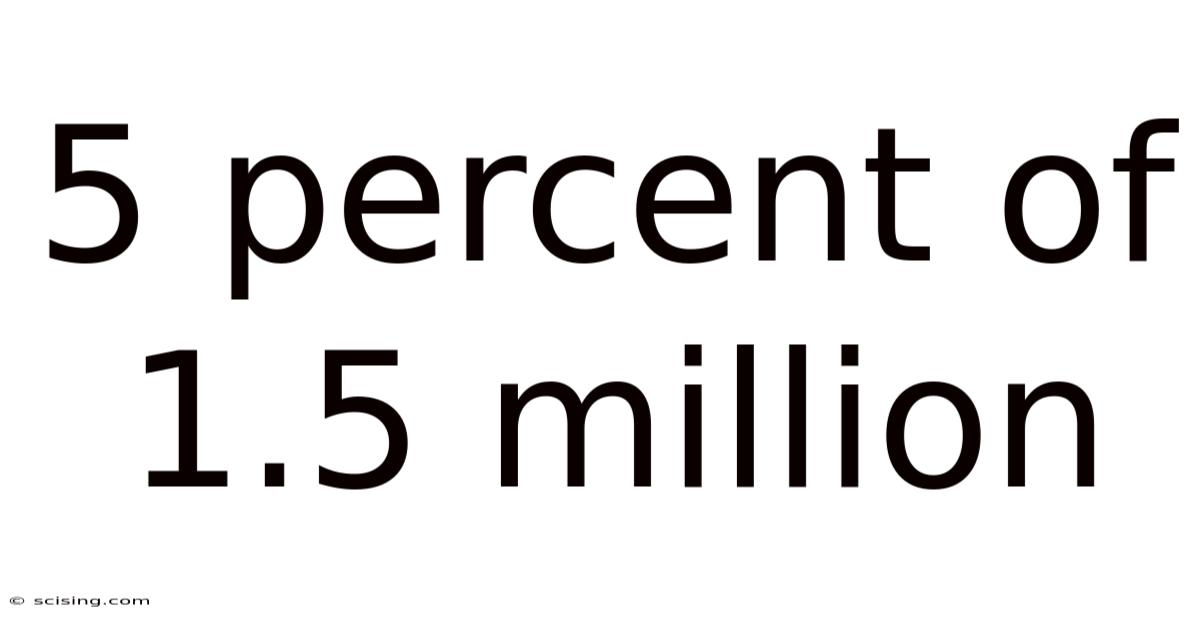
Table of Contents
Decoding 5 Percent of 1.5 Million: A Comprehensive Guide
Calculating percentages is a fundamental skill applicable across various fields, from everyday budgeting to complex financial analysis. This article delves into the seemingly simple calculation of 5% of 1.5 million, exploring different methods, practical applications, and the underlying mathematical principles. Understanding this calculation isn't just about getting the right answer; it's about grasping the conceptual framework that empowers you to tackle similar percentage problems with confidence. This guide will cover multiple approaches, ensuring a comprehensive understanding regardless of your mathematical background.
Understanding Percentages: A Refresher
Before diving into the calculation, let's refresh our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred." So, 5% means 5 out of 100, or 5/100, which simplifies to 1/20 as a fraction or 0.05 as a decimal. This fundamental understanding is key to solving percentage problems efficiently.
Method 1: The Decimal Method
This is arguably the most straightforward method, especially when dealing with larger numbers like 1.5 million. We convert the percentage to its decimal equivalent and then multiply it by the original number.
-
Step 1: Convert the percentage to a decimal. 5% is equal to 0.05 (5 divided by 100).
-
Step 2: Multiply the decimal by the original number. 0.05 * 1,500,000 = 75,000
Therefore, 5% of 1.5 million is 75,000.
This method leverages the power of decimal multiplication, making it computationally efficient, particularly when using calculators or spreadsheets.
Method 2: The Fraction Method
This method utilizes the fractional representation of the percentage. While slightly more involved, it reinforces the underlying mathematical concepts.
-
Step 1: Express the percentage as a fraction. 5% is equivalent to 5/100, which simplifies to 1/20.
-
Step 2: Multiply the fraction by the original number. (1/20) * 1,500,000 = 1,500,000 / 20
-
Step 3: Simplify the fraction. Dividing 1,500,000 by 20 gives us 75,000.
Again, we arrive at the answer: 5% of 1.5 million is 75,000. This method emphasizes the fractional nature of percentages, providing a deeper understanding of the underlying mathematical relationships.
Method 3: Using Proportions
This method involves setting up a proportion to solve for the unknown value. This approach is particularly useful for visualizing the relationship between the percentage and the whole.
-
Step 1: Set up a proportion. We can represent the problem as a proportion: 5/100 = x/1,500,000, where 'x' represents 5% of 1.5 million.
-
Step 2: Cross-multiply. This gives us 100x = 5 * 1,500,000 = 7,500,000.
-
Step 3: Solve for x. Divide both sides by 100: x = 7,500,000 / 100 = 75,000.
The result, once again, confirms that 5% of 1.5 million is 75,000. This method provides a visual representation of the percentage as a ratio, enhancing conceptual understanding.
Real-World Applications: Where Does This Calculation Matter?
Understanding how to calculate 5% of 1.5 million isn't just an academic exercise; it has numerous practical applications in various real-world scenarios:
-
Finance: Calculating interest on a large loan or investment. Imagine a loan of 1.5 million with a 5% interest rate; the annual interest would be 75,000. Similarly, a 5% return on a 1.5 million investment would yield 75,000.
-
Sales and Marketing: Determining sales commissions or discounts. A sales team achieving 1.5 million in sales might earn a 5% commission, totaling 75,000. A 5% discount on a 1.5 million product would reduce the price by 75,000.
-
Budgeting and Allocation: Determining a specific percentage of a large budget. A company with a 1.5 million annual budget might allocate 5% (75,000) to research and development.
-
Taxation: Calculating a specific tax percentage on a large income or property value. A 5% tax on a 1.5 million property would amount to 75,000.
-
Data Analysis: In statistical analysis, calculating percentages of large datasets is essential for drawing meaningful conclusions. For example, if a survey of 1.5 million people showed 5% support for a particular candidate, that represents 75,000 supporters.
These are just a few examples; the ability to calculate percentages accurately is crucial for informed decision-making across diverse professional fields.
Beyond the Basics: Understanding Percentage Increases and Decreases
While we've focused on calculating a simple percentage, it's important to understand how to calculate percentage increases and decreases. This is particularly relevant in financial contexts.
Let's say a value of 1.5 million increases by 5%. We first calculate the 5% increase (75,000) and then add it to the original value: 1,500,000 + 75,000 = 1,575,000.
Conversely, if the value decreases by 5%, we calculate the 5% decrease (75,000) and then subtract it from the original value: 1,500,000 - 75,000 = 1,425,000.
Mastering these calculations is vital for interpreting financial reports, understanding economic trends, and making sound financial decisions.
Dealing with More Complex Percentage Calculations
The principles discussed here can be extended to more complex percentage calculations. For instance, if you needed to calculate 7.5% of 1.5 million, you would simply convert 7.5% to its decimal equivalent (0.075) and multiply it by 1,500,000. The same logic applies to any percentage value.
The key is to break down the problem into manageable steps: convert the percentage to a decimal or fraction, then perform the multiplication. Always double-check your work to ensure accuracy.
Frequently Asked Questions (FAQ)
Q: What is the easiest way to calculate 5% of 1.5 million?
A: The decimal method is generally the easiest: convert 5% to 0.05 and multiply by 1,500,000.
Q: Can I use a calculator for this calculation?
A: Absolutely! Calculators are highly recommended, especially for larger numbers.
Q: What if I need to calculate a different percentage of 1.5 million?
A: Follow the same methods, substituting the desired percentage for 5%. Convert the percentage to a decimal or fraction and multiply by 1,500,000.
Q: What are some common mistakes to avoid when calculating percentages?
A: Common mistakes include incorrect decimal conversion, errors in multiplication, and forgetting to add or subtract when dealing with percentage increases or decreases. Always double-check your work.
Conclusion: Mastering Percentages for a Brighter Future
Calculating 5% of 1.5 million, while seemingly simple, underscores the importance of understanding fundamental mathematical concepts. This calculation has wide-ranging applications in personal finance, business, and data analysis. By mastering these methods, you equip yourself with a valuable skill applicable across many facets of life and work. Remember to practice regularly, and soon, calculating percentages will become second nature. The ability to confidently handle percentage calculations empowers you to make informed decisions, interpret data effectively, and navigate the complexities of the numerical world with ease. This foundational skill is an invaluable asset in both professional and personal settings.
Latest Posts
Latest Posts
-
Use Ziggurat In A Sentence
Sep 25, 2025
-
Mph To Meters Per Minute
Sep 25, 2025
-
Chapter 2 Summary Great Gatsby
Sep 25, 2025
-
Visual Aids For A Speech
Sep 25, 2025
-
Surface Area Of Hexagonal Prism
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 5 Percent Of 1.5 Million . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.