4 Out Of 20 Percentage
scising
Sep 21, 2025 · 6 min read
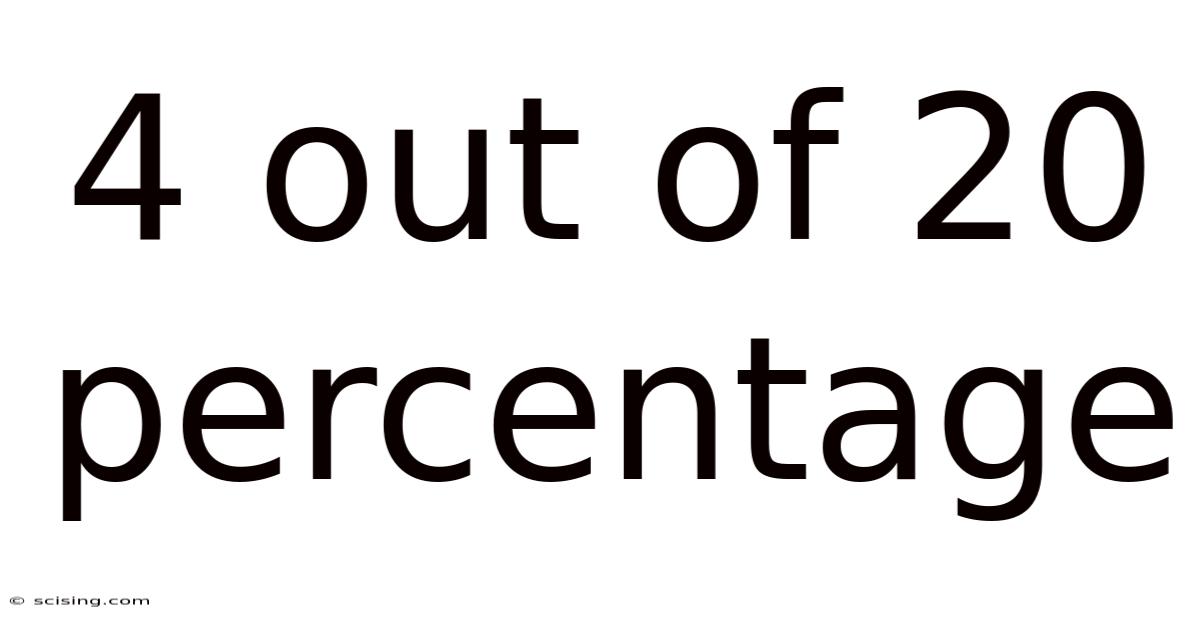
Table of Contents
Decoding "4 out of 20": Understanding Percentages and Their Applications
Understanding percentages is a fundamental skill applicable across various aspects of life, from calculating grades and discounts to comprehending financial reports and statistical data. This article delves deep into the seemingly simple concept of "4 out of 20," explaining its calculation, its representation as a percentage, and its broader implications within the realm of mathematics and real-world applications. We'll explore different ways to approach this problem, emphasizing the underlying principles to build a strong foundation in percentage calculations.
Understanding the Basics: Fractions, Decimals, and Percentages
Before we tackle "4 out of 20," let's establish a firm understanding of the interconnectedness of fractions, decimals, and percentages. They are simply different ways of expressing the same quantitative relationship.
-
Fraction: A fraction represents a part of a whole. In our case, "4 out of 20" is written as the fraction 4/20. The top number (4) is the numerator, representing the part, and the bottom number (20) is the denominator, representing the whole.
-
Decimal: A decimal is a way of expressing a fraction using a base-10 system. To convert a fraction to a decimal, you divide the numerator by the denominator. In this example, 4 ÷ 20 = 0.2.
-
Percentage: A percentage is a fraction expressed as parts per hundred. It's denoted by the symbol "%". To convert a decimal to a percentage, you multiply by 100. In our example, 0.2 x 100 = 20%. Therefore, 4 out of 20 is equivalent to 20%.
Calculating "4 out of 20" as a Percentage: Step-by-Step Guide
Let's break down the calculation of "4 out of 20" as a percentage into clear, concise steps:
Step 1: Express as a Fraction
The initial representation is already a fraction: 4/20.
Step 2: Simplify the Fraction (Optional but Recommended)
Simplifying the fraction makes the subsequent calculations easier. Both the numerator and denominator are divisible by 4:
4 ÷ 4 = 1 20 ÷ 4 = 5
The simplified fraction is 1/5.
Step 3: Convert the Fraction to a Decimal
Divide the numerator by the denominator:
1 ÷ 5 = 0.2
Step 4: Convert the Decimal to a Percentage
Multiply the decimal by 100:
0.2 x 100 = 20%
Therefore, 4 out of 20 is equal to 20%.
Real-World Applications: Where Percentages Matter
The concept of "4 out of 20," and percentage calculations in general, are incredibly versatile and applicable in numerous real-world scenarios. Let's explore a few examples:
-
Academic Performance: Imagine a student scoring 4 out of 20 on a quiz. This translates to a 20% score, indicating a significant need for improvement. This percentage allows for easy comparison with other students and provides a clear measure of their understanding of the subject matter.
-
Sales and Discounts: A store offering a 20% discount on an item is essentially offering a reduction equivalent to 4 out of 20 of the original price. This is a common application of percentages in marketing and retail.
-
Financial Analysis: In finance, percentages are ubiquitous. Analyzing investment returns, understanding interest rates, or calculating profit margins all rely heavily on percentage calculations. A 20% increase in profit, for instance, would be a positive indicator of growth.
-
Data Interpretation: In statistics and data analysis, percentages are frequently used to present complex information in a clear and concise way. For example, a survey revealing that 20% of respondents prefer a particular brand provides a readily understandable summary of the data.
-
Probability and Statistics: The probability of an event occurring is often expressed as a percentage. If there's a 20% chance of rain, it means that out of 100 similar situations, rain might occur in 20.
Beyond the Basics: Advanced Percentage Calculations
While understanding "4 out of 20" provides a foundation, let's delve into more complex percentage calculations that build upon this fundamental concept:
-
Calculating Percentage Increase or Decrease: This involves determining the percentage change between two values. For example, if a quantity increases from 20 to 24, the percentage increase is calculated as: [(24 - 20) / 20] x 100 = 20%. Similarly, a decrease can be calculated.
-
Finding the Original Value: If you know the percentage and the final value, you can determine the original value. For example, if a price after a 20% discount is $16, the original price can be calculated as: $16 / (1 - 0.20) = $20.
-
Calculating Percentages of Percentages: This involves working with nested percentages. For example, finding 20% of 20% of a value requires multiple percentage calculations.
Addressing Common Misconceptions about Percentages
Several common misconceptions surround percentages that can lead to errors in calculations and interpretations:
-
Confusing Percentage Points with Percentages: A change from 20% to 22% is a 2 percentage point increase, not a 10% increase. This distinction is critical in accurate interpretation.
-
Incorrectly Adding or Subtracting Percentages: Percentages cannot be directly added or subtracted unless they refer to the same base value.
-
Misunderstanding Percentage Changes over Multiple Periods: A 10% increase followed by a 10% decrease does not result in the original value; it results in a slightly lower value due to the compounding effect.
Frequently Asked Questions (FAQ)
Q1: How can I quickly calculate percentages in my head?
A1: For simple percentages like 10%, 20%, 25%, and 50%, it's easy to mentally calculate them. For 10%, simply move the decimal point one place to the left. For 20%, double the 10% value, and so on. Practice will make this faster. For more complex percentages, using a calculator is always recommended for accuracy.
Q2: What are some helpful tools or resources for practicing percentage calculations?
A2: Numerous online calculators, educational websites, and apps provide interactive exercises and quizzes to improve your understanding and proficiency in percentage calculations. Many textbooks also contain ample practice problems.
Q3: Why are percentages so important in everyday life?
A3: Percentages provide a standardized and easily understandable way to compare quantities, express proportions, and interpret data. Their applications span various fields, from finance and shopping to education and scientific research. Understanding percentages empowers you to make informed decisions and navigate various aspects of life more effectively.
Conclusion: Mastering the Art of Percentages
Understanding "4 out of 20" as 20% is just the starting point of a journey into the world of percentages. This article has provided a comprehensive exploration of percentages, from their basic definitions to their advanced applications. Mastering the concepts discussed here will equip you with a valuable skillset applicable across numerous domains. Remember that consistent practice and a clear understanding of the underlying principles are key to developing proficiency in percentage calculations and confidently applying them in diverse real-world contexts. The ability to calculate and interpret percentages is not just a mathematical skill; it’s a crucial life skill that enhances your understanding of the world around you.
Latest Posts
Latest Posts
-
Real Life Exponential Function Examples
Sep 21, 2025
-
Geometric Mean Of Right Triangles
Sep 21, 2025
-
How Are Rift Valleys Made
Sep 21, 2025
-
Is Salad Homogeneous Or Heterogeneous
Sep 21, 2025
-
Panic Of 1837 Apush Definition
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 4 Out Of 20 Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.