4 Divided By 1 4
scising
Sep 06, 2025 · 5 min read
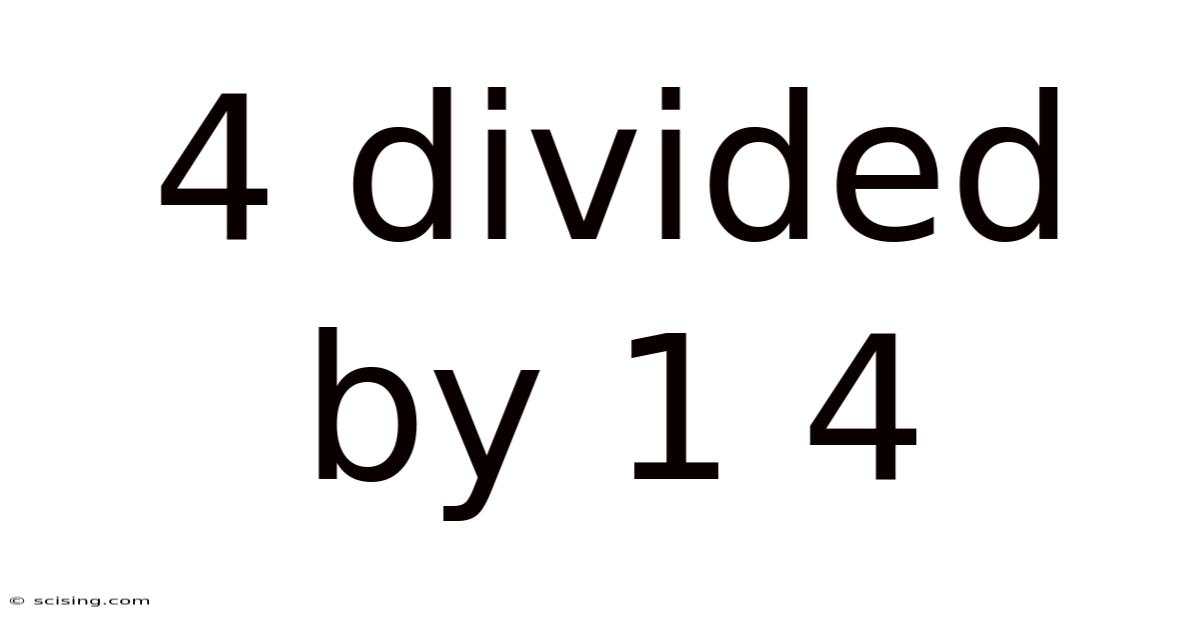
Table of Contents
Deconstructing 4 ÷ 1 ¼: A Deep Dive into Division with Fractions
This article explores the seemingly simple yet conceptually rich problem of 4 divided by 1 ¼ (four divided by one and one-quarter). We'll unpack the process step-by-step, examining different methods, explaining the underlying mathematical principles, and addressing common misconceptions. Understanding this seemingly basic calculation is fundamental to mastering more complex division problems involving fractions and decimals. We will cover various approaches, ensuring you gain a comprehensive understanding and the confidence to tackle similar problems independently.
Understanding the Problem: 4 ÷ 1 ¼
Before diving into the solution, let's clearly define the problem. We are tasked with dividing the whole number 4 by the mixed number 1 ¼. This means we want to find out how many times 1 ¼ fits into 4. This seemingly simple division problem touches upon fundamental concepts in arithmetic, including:
- Division: The process of splitting a quantity into equal parts.
- Fractions: Numbers representing parts of a whole.
- Mixed Numbers: Numbers consisting of a whole number and a fraction (e.g., 1 ¼).
- Improper Fractions: Fractions where the numerator is greater than or equal to the denominator.
Method 1: Converting to Improper Fractions
This method is arguably the most straightforward and widely used. It involves converting both the whole number and the mixed number into improper fractions, then proceeding with the division.
Step 1: Convert the Mixed Number to an Improper Fraction:
To convert 1 ¼ to an improper fraction, we multiply the whole number (1) by the denominator (4) and add the numerator (1). This result becomes the new numerator, while the denominator remains the same.
1 ¼ = (1 x 4 + 1) / 4 = 5/4
Step 2: Convert the Whole Number to an Improper Fraction:
Any whole number can be expressed as a fraction with a denominator of 1. Therefore, 4 can be written as 4/1.
Step 3: Perform the Division:
Dividing fractions involves multiplying the first fraction by the reciprocal of the second fraction. The reciprocal of a fraction is obtained by swapping the numerator and the denominator.
4/1 ÷ 5/4 = 4/1 x 4/5 = 16/5
Step 4: Simplify the Result:
The improper fraction 16/5 can be converted back into a mixed number by dividing the numerator (16) by the denominator (5).
16 ÷ 5 = 3 with a remainder of 1.
Therefore, 16/5 = 3 1/5
Conclusion: 4 ÷ 1 ¼ = 3 1/5
Method 2: Using Long Division
While less intuitive for fractions, long division provides a visual representation of the process. This method requires converting the mixed number into a decimal.
Step 1: Convert the Mixed Number to a Decimal:
1 ¼ is equivalent to 1.25.
Step 2: Perform Long Division:
Now we perform the long division of 4 by 1.25.
3.2
1.25 | 4.00
-3.75
0.250
-0.250
0
Step 3: Interpret the Result:
The result of the long division is 3.2. This decimal can be converted back to a fraction: 3.2 = 3 2/10 = 3 1/5.
Conclusion: 4 ÷ 1 ¼ = 3.2 = 3 1/5
Method 3: Repeated Subtraction
This method, although less efficient for larger numbers, offers a visual understanding of division. It involves repeatedly subtracting the divisor (1 ¼) from the dividend (4) until the remainder is less than the divisor.
Step 1: Repeated Subtraction:
- 4 - 1 ¼ = 2 ¾
- 2 ¾ - 1 ¼ = 1 ½
- 1 ½ - 1 ¼ = ¼
We subtracted 1 ¼ three times before the remaining value (¼) was less than 1 ¼.
Step 2: Interpret the Result:
We successfully subtracted 1 ¼ three times, leaving a remainder of ¼. This means 1 ¼ fits into 4 three times with a remainder of ¼ of 1 ¼. To express this as a fraction, we have 3 and ¼ of 1 ¼, which is (1/4)/(5/4)=1/5 . Therefore, the result is 3 1/5.
Conclusion: 4 ÷ 1 ¼ = 3 1/5
Mathematical Explanation: The Reciprocal and its Significance
The core principle underlying the conversion of division into multiplication using reciprocals is rooted in the fundamental properties of fractions and their multiplicative inverses.
- Multiplicative Inverse (Reciprocal): The reciprocal of a number is the number that, when multiplied by the original number, results in 1. For example, the reciprocal of 5/4 is 4/5 because (5/4) x (4/5) = 1.
When we divide by a fraction, we are essentially asking "how many times does this fraction fit into the whole number?" Multiplying by the reciprocal effectively reverses this process, making the calculation much more manageable.
Common Mistakes and Misconceptions
- Incorrectly converting mixed numbers to improper fractions: Carefully follow the steps; a single error can significantly affect the final answer.
- Failing to properly take the reciprocal: Remember to switch the numerator and denominator of the fraction you are dividing by.
- Mistakes in simplifying fractions: Always reduce your final answer to its simplest form.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to solve this problem?
A: Yes, you can enter 4 ÷ 1.25 into a calculator to obtain the decimal answer 3.2, which can then be converted to the fraction 3 1/5.
Q: Why are there multiple methods to solve this problem?
A: Different methods cater to diverse learning styles and provide a deeper understanding of the underlying mathematical concepts.
Q: What if the numbers were larger or involved more complex fractions?
A: The principles remain the same. Convert to improper fractions, take the reciprocal, and simplify. Long division may become more tedious.
Conclusion: Mastering Fraction Division
This comprehensive exploration of 4 ÷ 1 ¼ demonstrates that seemingly simple problems can reveal profound insights into fundamental mathematical principles. By understanding the various methods – conversion to improper fractions, long division, and repeated subtraction – you develop a versatile toolkit for tackling fraction division problems of any complexity. Remember the importance of accurate conversions, correctly applying the reciprocal, and simplifying the final answer. With practice and a solid grasp of these principles, you'll confidently navigate the world of fraction division and beyond. The ability to comfortably work with fractions is a crucial skill that forms the cornerstone for more advanced mathematical concepts in algebra, calculus, and beyond. Mastering this seemingly simple problem unlocks a significant understanding of fundamental mathematical operations.
Latest Posts
Latest Posts
-
Scientific Name For A Spider
Sep 06, 2025
-
What Is Assimilation In Biology
Sep 06, 2025
-
Ares God Of War Symbol
Sep 06, 2025
-
What Does Cer Stand For
Sep 06, 2025
-
96 Degrees F To C
Sep 06, 2025
Related Post
Thank you for visiting our website which covers about 4 Divided By 1 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.