4 20 As A Percent
scising
Sep 08, 2025 · 5 min read
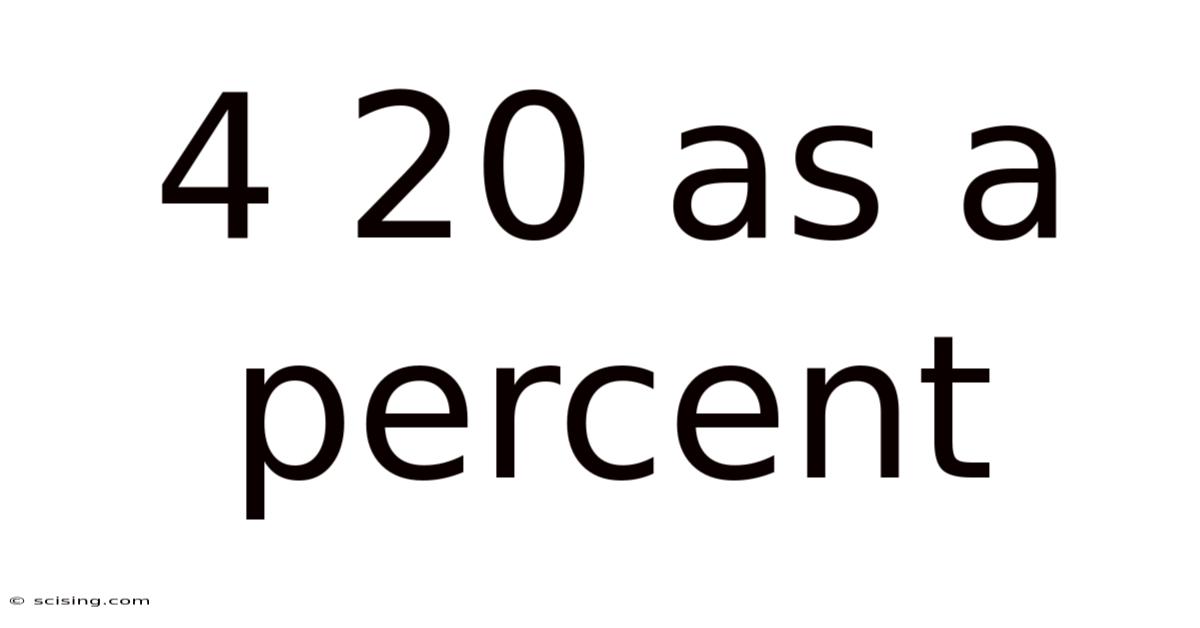
Table of Contents
Decoding 4/20 as a Percentage: A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics with applications spanning various fields, from everyday budgeting to complex scientific calculations. This article delves into the seemingly simple task of converting the fraction 4/20 into a percentage, exploring the underlying concepts and providing a thorough understanding of the process. We'll cover the calculation methods, provide real-world examples, address common misconceptions, and answer frequently asked questions to ensure a comprehensive grasp of this important topic.
Understanding Fractions and Percentages
Before diving into the conversion of 4/20, let's revisit the basic definitions. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts we have, while the denominator shows the total number of parts the whole is divided into.
A percentage, on the other hand, is a way of expressing a number as a fraction of 100. The symbol "%" represents "per hundred" or "out of 100." Percentages are widely used because they provide a standardized way to compare proportions and make them easily understandable.
Converting 4/20 to a Percentage: Step-by-Step Guide
There are two primary methods to convert the fraction 4/20 to a percentage:
Method 1: Simplifying the Fraction First
This method involves simplifying the fraction to its lowest terms before converting it to a percentage. This simplifies the calculation and makes it easier to understand.
-
Simplify the Fraction: The fraction 4/20 can be simplified by finding the greatest common divisor (GCD) of the numerator (4) and the denominator (20). The GCD of 4 and 20 is 4. Dividing both the numerator and the denominator by 4, we get:
4 ÷ 4 / 20 ÷ 4 = 1/5
-
Convert the Simplified Fraction to a Decimal: To convert the simplified fraction 1/5 to a decimal, we divide the numerator (1) by the denominator (5):
1 ÷ 5 = 0.2
-
Convert the Decimal to a Percentage: To convert the decimal 0.2 to a percentage, we multiply it by 100 and add the percentage sign (%):
0.2 × 100 = 20%
Therefore, 4/20 is equal to 20%.
Method 2: Direct Conversion to Percentage
This method involves directly converting the fraction to a percentage without simplifying it first.
-
Convert the Fraction to a Decimal: Divide the numerator (4) by the denominator (20):
4 ÷ 20 = 0.2
-
Convert the Decimal to a Percentage: Multiply the decimal (0.2) by 100 and add the percentage sign (%):
0.2 × 100 = 20%
This method yields the same result as Method 1, demonstrating that both approaches are valid.
Real-World Applications of Percentage Calculations
The ability to convert fractions to percentages is crucial in many real-world scenarios:
-
Calculating Discounts: If a store offers a 20% discount on an item, you can easily determine the discount amount by multiplying the original price by 0.2.
-
Analyzing Test Scores: If you answered 4 out of 20 questions correctly on a test, your score would be 20%.
-
Understanding Financial Statements: Financial reports often express various ratios and proportions as percentages, allowing for easy comparisons and analysis.
-
Interpreting Survey Results: Survey data is frequently presented as percentages to summarize findings and make them easily understandable.
-
Calculating Interest Rates: Interest rates on loans and investments are usually expressed as percentages.
Common Misconceptions about Percentages
Some common misunderstandings surrounding percentages include:
-
Adding Percentages Directly: You cannot simply add percentages directly unless they are based on the same whole. For example, a 10% increase followed by a 10% decrease does not result in the original value.
-
Confusing Percentage Change with Absolute Change: A percentage change reflects the proportional change, while an absolute change reflects the actual numerical difference. A small percentage change can represent a large absolute change depending on the initial value, and vice-versa.
-
Incorrect Interpretation of Percentage Points: Percentage points refer to the absolute difference between two percentages. For example, an increase from 20% to 25% is a 5 percentage point increase, not a 25% increase.
Mathematical Explanation: The Underlying Principle
The conversion from a fraction to a percentage fundamentally relies on the concept of proportionality. A percentage expresses a fraction in terms of a denominator of 100. Therefore, converting a fraction to a percentage involves finding the equivalent fraction with a denominator of 100.
Mathematically, the conversion can be expressed as:
(Numerator / Denominator) × 100 = Percentage
In the case of 4/20, this translates to:
(4 / 20) × 100 = 20%
The multiplication by 100 scales the fraction to express it as a part of 100, thereby obtaining the percentage equivalent.
Frequently Asked Questions (FAQ)
Q: What if the fraction does not simplify easily?
A: If the fraction does not simplify easily, you can still use Method 2 (direct conversion to a decimal and then to a percentage) without any issues. Calculators or other tools can assist in dividing the numerator by the denominator.
Q: Can negative fractions be converted to percentages?
A: Yes, negative fractions can be converted to percentages. The result will simply be a negative percentage. For example, -4/20 would be -20%.
Q: How can I check my answer?
A: You can verify your answer by converting the percentage back to a fraction. To do so, divide the percentage by 100 and simplify the resulting fraction. If it matches the original fraction, your conversion is correct.
Conclusion
Converting 4/20 to a percentage is a straightforward process, and understanding the different methods allows for flexibility and efficiency. This seemingly simple calculation underlies a crucial concept in mathematics with widespread practical implications. By mastering the conversion process and understanding the underlying principles, we gain a more robust foundation in numeracy and enhance our ability to solve a wide range of problems involving proportions and ratios in various aspects of life. Remember, practicing different examples and applying the concepts in real-world scenarios will solidify your understanding and make percentage calculations second nature.
Latest Posts
Latest Posts
-
What Color Is Gatsbys Car
Sep 08, 2025
-
Example Of A Role Strain
Sep 08, 2025
-
Symmetric Property Of Equality Example
Sep 08, 2025
-
Theme Of Annabel Lee Poem
Sep 08, 2025
-
Distinction Between Growth And Development
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about 4 20 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.