35 Of What Is 14
scising
Sep 20, 2025 · 5 min read
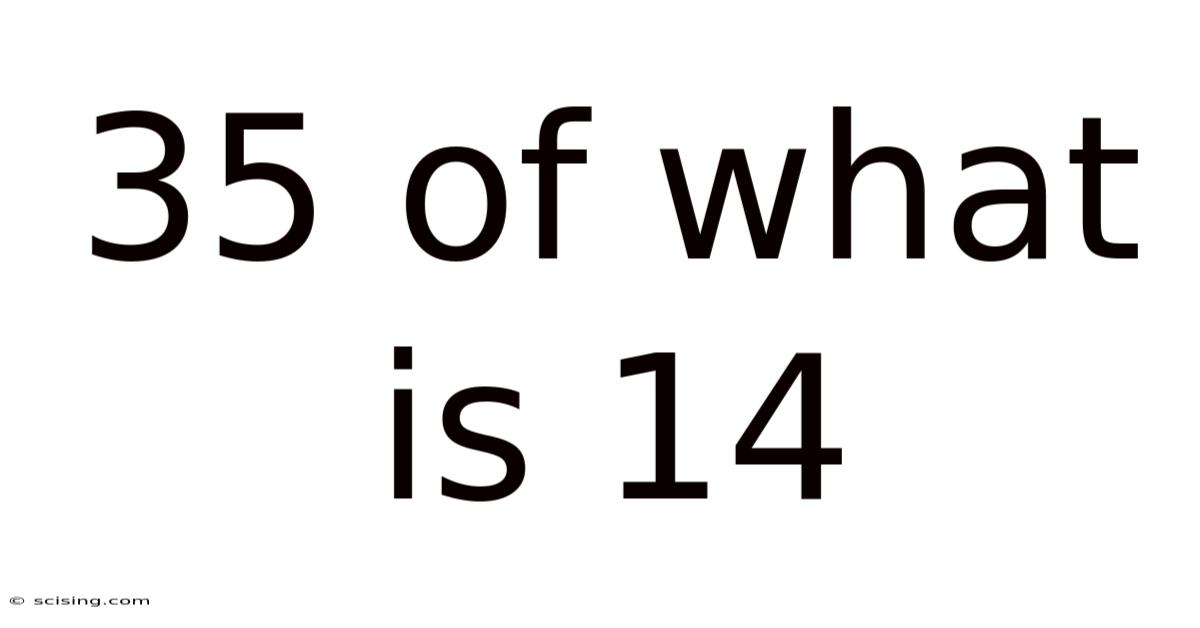
Table of Contents
Decoding the Fraction: 35 of 14 – A Comprehensive Guide
Understanding fractions is a fundamental skill in mathematics, crucial for navigating everyday life and excelling in further studies. This article delves deep into the seemingly simple question: "What is 35 of 14?" We'll explore various methods for solving this problem, explain the underlying mathematical concepts, and offer practical applications to solidify your understanding. This comprehensive guide will not only provide the answer but will also equip you with the tools to tackle similar fraction problems confidently.
Understanding the Problem: 35 of 14
The phrase "35 of 14" translates mathematically to finding 3/5 of 14. This means we need to determine what portion of 14 represents three-fifths of its total value. This type of problem involves the concept of multiplication with fractions, a core component of arithmetic.
Method 1: Converting the Fraction to a Decimal
One approach to solving this problem involves converting the fraction 3/5 into its decimal equivalent. To do this, we simply divide the numerator (3) by the denominator (5):
3 ÷ 5 = 0.6
Now, we multiply this decimal by 14:
0.6 x 14 = 8.4
Therefore, 3/5 of 14 is 8.4.
Method 2: Direct Multiplication with Fractions
A more direct method involves performing the multiplication of the fraction and the whole number directly. This method is particularly useful when dealing with more complex fractions. We multiply the numerator of the fraction by the whole number and then divide the result by the denominator:
(3 x 14) ÷ 5 = 42 ÷ 5 = 8.4
Again, we arrive at the answer: 8.4
Method 3: Finding the Fraction of a Whole Number using Simplification
Before performing the multiplication, we can simplify the fraction if possible. Although 3/5 is already in its simplest form, this step is crucial when dealing with more complex fractions. This simplifies the calculation, reducing the risk of errors.
Method 4: Visual Representation – Understanding Fractions through Parts of a Whole
Visualizing fractions helps build intuitive understanding. Imagine a rectangle divided into five equal parts. Each part represents 1/5 of the whole. To find 3/5, we simply shade three of these parts. If the whole rectangle represents 14, we need to determine the value of those three shaded parts.
Since the whole rectangle (14) is divided into five equal parts, each part represents 14 ÷ 5 = 2.8.
Therefore, three parts (3/5) would represent 2.8 x 3 = 8.4.
This visual method effectively demonstrates the concept of a fraction as a part of a whole.
Real-World Applications of Fractions: Why This Matters
The ability to solve fraction problems, like finding 3/5 of 14, is not merely an academic exercise. It has numerous practical applications in daily life:
-
Cooking and Baking: Recipes often call for fractional amounts of ingredients. Understanding fractions ensures you accurately measure ingredients, leading to successful results. For example, a recipe might call for 2/3 of a cup of flour.
-
Shopping and Budgeting: Calculating discounts, sales tax, or splitting bills often involves fractional computations. Being proficient in fractions ensures you're making informed financial decisions. Imagine calculating a 20% discount on a $50 item – that’s 1/5 of $50.
-
Construction and Engineering: Precision and accuracy are paramount in these fields. Calculations involving fractions are critical for ensuring structures are built correctly and efficiently. Measurements might require fractions of inches or meters.
-
Data Analysis and Statistics: Understanding fractions is essential for interpreting data and statistics. Graphs and charts often represent data as fractions or percentages.
-
Everyday Problem Solving: From dividing a pizza among friends to understanding proportions in various contexts, fractions are an indispensable part of daily problem-solving.
Addressing Common Misconceptions about Fractions
Several common misconceptions can hinder understanding and problem-solving with fractions:
-
Treating fractions as separate numbers: It's crucial to remember that a fraction represents a single value, not two separate numbers. 3/5 is not 3 and 5, but rather 3 parts out of 5.
-
Incorrect order of operations: When dealing with mixed operations involving fractions, remember to follow the order of operations (PEMDAS/BODMAS) to ensure correct calculations.
-
Difficulty visualizing fractions: Visual aids such as diagrams and charts can significantly improve comprehension and make the concept of fractions more intuitive.
-
Inability to simplify fractions: Simplifying fractions (reducing them to their lowest terms) is a crucial skill that streamlines calculations and makes them easier to understand.
Expanding the Concept: Working with More Complex Fractions
While the problem “35 of 14” is relatively simple, the principles discussed can be extended to more complex fractional problems. For example, consider finding 7/12 of 24. The process remains the same:
-
Direct Multiplication: (7 x 24) ÷ 12 = 14
-
Simplification: Notice that 12 can be divided into 24 twice. Simplifying this beforehand gives: (7 x 2) = 14
Frequently Asked Questions (FAQ)
Q1: What if the whole number isn't divisible evenly by the denominator?
A1: Even if the whole number isn't evenly divisible by the denominator, the process remains the same. You'll simply end up with a decimal or a fraction as the answer. For example, 2/3 of 7 would be (2 x 7) ÷ 3 = 4.666...
Q2: How do I convert a mixed number (like 1 1/2) into an improper fraction?
A2: To convert a mixed number into an improper fraction, multiply the whole number by the denominator and add the numerator. The result becomes the new numerator, while the denominator remains the same. For example, 1 1/2 becomes (1 x 2 + 1)/2 = 3/2.
Q3: Can I use a calculator to solve these problems?
A3: Yes, calculators are helpful, especially for more complex fractions. However, understanding the underlying mathematical principles remains crucial.
Conclusion: Mastering Fractions for a Brighter Future
Mastering fractions is a vital skill that extends beyond the classroom, impacting various aspects of life. The seemingly simple question, "What is 3/5 of 14?", serves as a gateway to understanding the broader concepts of fractions, their practical applications, and the confidence to tackle more complex mathematical challenges. By employing the various methods discussed—direct multiplication, decimal conversion, and visual representation—you can confidently navigate the world of fractions and unlock a deeper understanding of mathematical principles. Remember, practice is key to solidifying your understanding and building confidence in your ability to solve fractional problems efficiently and accurately. So grab a pencil and paper and continue practicing! Remember, every step towards mathematical proficiency is a step towards a brighter future.
Latest Posts
Latest Posts
-
Why Is There Military Time
Sep 20, 2025
-
Green And Yellow Bracelet Meaning
Sep 20, 2025
-
Future Tense In German Language
Sep 20, 2025
-
Limit Of A Composite Function
Sep 20, 2025
-
Chemical To Mechanical Energy Examples
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 35 Of What Is 14 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.