3 Percent Of 3 Million
scising
Sep 15, 2025 · 5 min read
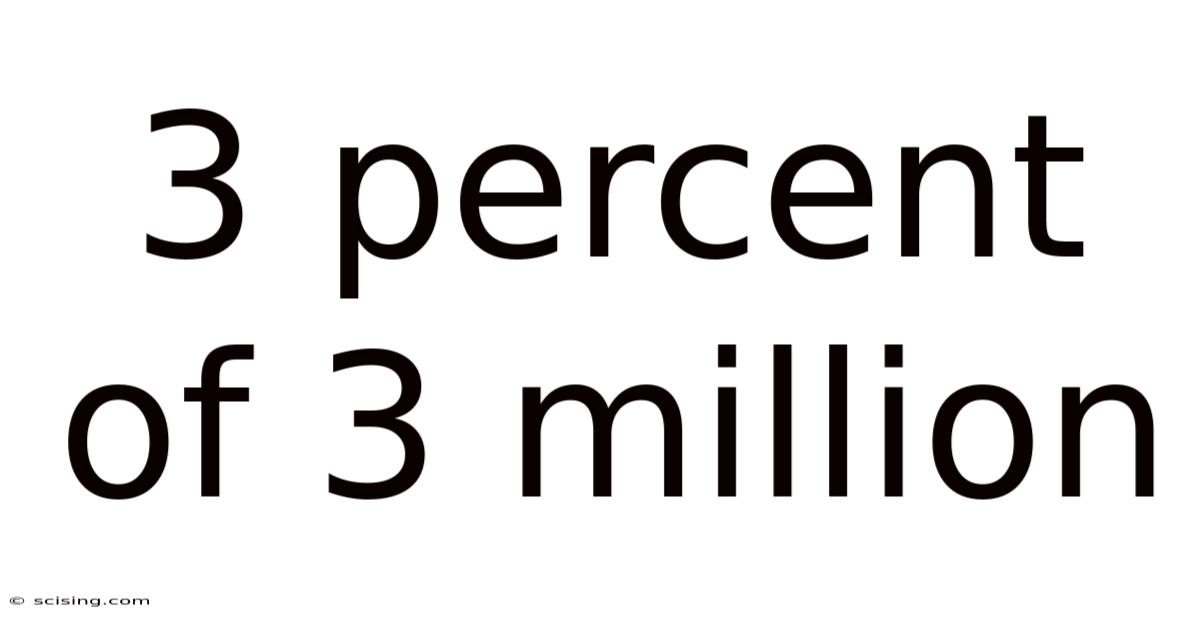
Table of Contents
Decoding 3 Percent of 3 Million: A Deep Dive into Percentages and Calculations
Finding 3 percent of 3 million might seem like a simple math problem, but understanding the underlying concepts and exploring different calculation methods can significantly enhance your mathematical skills and problem-solving abilities. This article will not only provide you with the solution but also delve into the intricacies of percentage calculations, offering practical examples and exploring related concepts. This is crucial for various applications, from everyday budgeting and financial planning to more complex scientific and business calculations.
Understanding Percentages: The Foundation
Before diving into the calculation, let's refresh our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Therefore, 3 percent (3%) can be written as 3/100 or 0.03. This simple representation is the key to unlocking efficient percentage calculations.
Method 1: The Direct Calculation Method
The most straightforward approach to finding 3 percent of 3 million is to convert the percentage to a decimal and then multiply it by the total amount.
-
Convert the percentage to a decimal: 3% = 3/100 = 0.03
-
Multiply the decimal by the total amount: 0.03 * 3,000,000 = 90,000
Therefore, 3 percent of 3 million is 90,000.
Method 2: The Fraction Method
Alternatively, we can use the fraction representation of the percentage.
-
Express the percentage as a fraction: 3% = 3/100
-
Multiply the fraction by the total amount: (3/100) * 3,000,000
-
Simplify the calculation: This can be simplified by canceling out common factors. 100 goes into 3,000,000 30,000 times. Therefore, the equation becomes: 3 * 30,000 = 90,000.
Again, the result is 90,000.
Method 3: Using Proportions
The concept of proportions provides another effective method for solving percentage problems. A proportion establishes a relationship between two ratios. We can set up a proportion to solve for the unknown value (x), which represents 3% of 3,000,000.
-
Set up the proportion: 3/100 = x/3,000,000
-
Cross-multiply: 100x = 3 * 3,000,000
-
Solve for x: 100x = 9,000,000 => x = 9,000,000 / 100 = 90,000
This method confirms our previous results: 3% of 3 million is 90,000.
Real-World Applications: Where Percentage Calculations Matter
Understanding how to calculate percentages is not just an academic exercise; it's a vital skill with numerous real-world applications. Here are just a few examples:
-
Finance: Calculating interest on loans, savings accounts, and investments; determining discounts and sales tax; analyzing financial statements and budgets. Imagine calculating the interest earned on a 3 million dollar investment; this principle is directly applicable.
-
Business: Analyzing market share, calculating profit margins, determining sales growth, managing inventory, and projecting future revenue. Understanding a 3% increase in sales from a base of 3 million dollars would be a crucial metric for many businesses.
-
Science: Expressing experimental results, calculating statistical probabilities, and determining the concentration of substances.
-
Everyday Life: Calculating tips at restaurants, determining the discount on sale items, understanding tax rates, and even comparing prices of different products.
Expanding the Concept: Beyond Simple Percentages
While we've focused on calculating 3% of 3 million, the principles can be extended to any percentage and any quantity. Let's explore some variations:
-
Finding a different percentage: Suppose we want to find 7% of 3 million. We'd simply replace 0.03 with 0.07 in our calculations, yielding 210,000.
-
Calculating a different base amount: If we wanted to find 3% of a different number, say 5 million, we'd replace 3,000,000 with 5,000,000, resulting in 150,000.
-
Inverse Percentage Calculations: We might also want to determine what percentage a certain amount represents of a larger quantity. For instance, if we know that 90,000 is a certain percentage of 3 million, we can set up the proportion and solve: x/100 = 90,000/3,000,000, leading to x = 3%.
Advanced Applications and Implications
The ability to calculate percentages efficiently opens doors to more complex mathematical and financial concepts. For instance:
-
Compound Interest: Calculating compound interest involves repeated percentage calculations over time. Understanding the fundamentals of simple percentage calculations is essential for grasping the more complex dynamics of compound interest.
-
Statistical Analysis: Percentages play a critical role in statistical analysis, allowing us to express data as proportions and probabilities. Understanding percentages is foundational for interpreting data correctly.
-
Financial Modeling: Sophisticated financial models rely heavily on percentage calculations to project future revenues, expenses, and profits.
Frequently Asked Questions (FAQ)
Q1: What if I need to calculate a percentage that involves decimals, for example, 3.5% of 3 million?
A1: The process remains the same. Convert 3.5% to a decimal (0.035) and multiply it by 3,000,000. The result will be 105,000.
Q2: Are there any shortcuts or tricks for mental calculation of percentages?
A2: Yes! For simple percentages like 10%, 5%, or 1%, you can perform mental calculations. 10% is simply moving the decimal point one place to the left. 5% is half of 10%, and 1% is one-tenth of 10%. These mental shortcuts can significantly speed up calculations, especially with larger numbers.
Q3: How can I improve my skills in percentage calculations?
A3: Practice is key! Work through various examples, including those with larger numbers and decimals. You can find plenty of practice problems online or in textbooks. Understanding the underlying concepts—converting percentages to decimals and fractions—is crucial.
Q4: What are some common errors to avoid when calculating percentages?
A4: Common errors include incorrectly converting percentages to decimals, forgetting to multiply by the base amount, and making calculation errors. Carefully review your work and use a calculator when necessary. Pay close attention to decimal places.
Conclusion: Mastering Percentages – A Valuable Skill
Calculating 3 percent of 3 million, resulting in 90,000, is a straightforward but foundational calculation. Understanding this simple example unlocks a world of applications across various fields. Mastering percentage calculations is not just about getting the right answer; it's about developing a deeper understanding of mathematical concepts and their real-world implications. By understanding the different methods, practicing regularly, and being aware of potential pitfalls, you can confidently tackle more complex percentage problems and harness their power in your daily life and professional endeavors. Remember, the key is not just memorizing formulas but comprehending the fundamental principles behind them. This understanding will empower you to solve a vast array of numerical challenges efficiently and accurately.
Latest Posts
Latest Posts
-
What Are The Expressed Powers
Sep 15, 2025
-
1 Liter Water To Grams
Sep 15, 2025
-
What Is Open In Spanish
Sep 15, 2025
-
Is Sand A Homogeneous Mixture
Sep 15, 2025
-
How Tall Is Darry Curtis
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 3 Percent Of 3 Million . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.