3 Out Of 8 Percentage
scising
Sep 19, 2025 · 6 min read
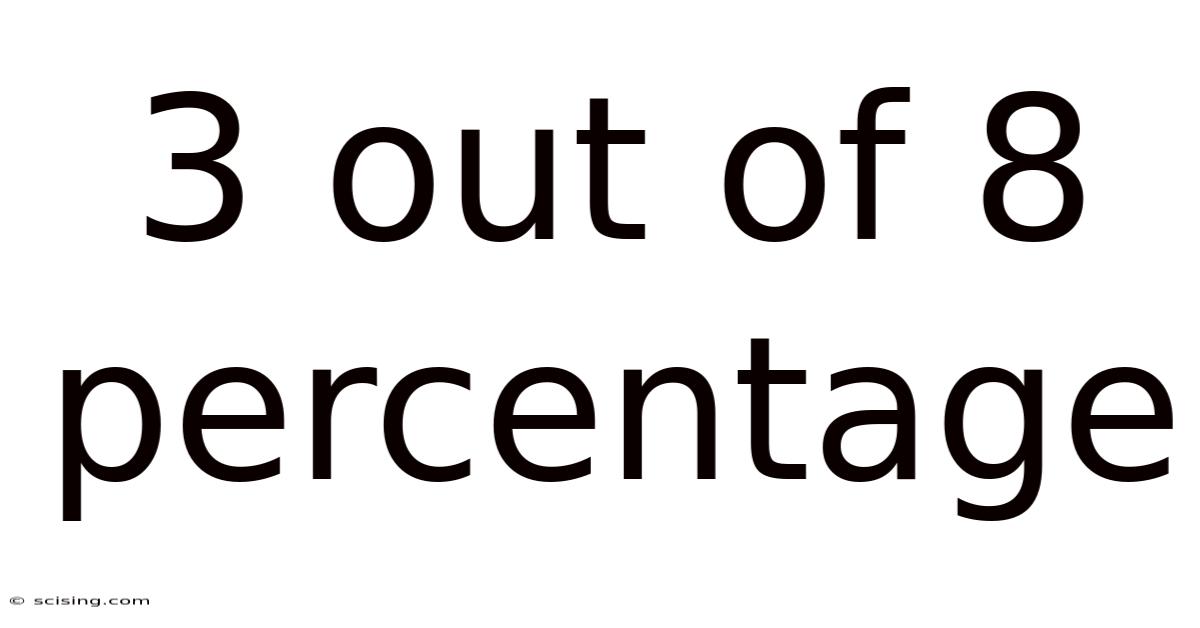
Table of Contents
Understanding 3 out of 8: A Deep Dive into Percentages and Proportions
Understanding percentages is a fundamental skill in many aspects of life, from calculating discounts in a store to interpreting data in scientific research. This article will delve into the seemingly simple calculation of "3 out of 8," exploring its various interpretations, practical applications, and the underlying mathematical concepts. We will move beyond a simple percentage calculation to explore the broader implications of ratios and proportions. This will equip you with a stronger understanding of how to approach similar problems and confidently interpret proportional relationships.
Introduction: The Basics of Percentages
A percentage is a way of expressing a number as a fraction of 100. It represents a portion of a whole. The phrase "3 out of 8" describes a ratio – a comparison of two quantities. To express this ratio as a percentage, we need to determine what fraction of the whole (8) the number 3 represents. This involves a straightforward calculation, but the understanding goes much deeper than just the numerical result. We'll explore that depth in this article.
Calculating 3 out of 8 as a Percentage: A Step-by-Step Guide
The calculation is quite simple:
-
Form the fraction: Express "3 out of 8" as a fraction: 3/8.
-
Convert to decimal: Divide the numerator (3) by the denominator (8): 3 ÷ 8 = 0.375
-
Convert to percentage: Multiply the decimal by 100: 0.375 x 100 = 37.5%
Therefore, 3 out of 8 is equal to 37.5%. This means that 3 represents 37.5% of the total quantity of 8.
Understanding Proportions and Ratios: Beyond the Simple Calculation
While the calculation above is straightforward, understanding the underlying principles of proportions and ratios is crucial for applying this knowledge in more complex situations.
-
Ratio: A ratio is a comparison of two or more quantities. In our case, the ratio is 3:8 (3 to 8). This ratio represents the relative sizes of the two quantities.
-
Proportion: A proportion is a statement that two ratios are equal. For example, 3/8 = x/100 is a proportion where we are solving for x (which is our percentage). Understanding proportions allows us to solve problems where we have a known ratio and need to find an equivalent ratio with different quantities.
Real-World Applications of 3 out of 8 (or 37.5%)
The application of understanding 3 out of 8, or its equivalent 37.5%, extends far beyond simple arithmetic. Consider these examples:
-
Test Scores: If a student answered 3 out of 8 questions correctly on a quiz, their score would be 37.5%. This provides a clear measure of their performance.
-
Survey Results: If 3 out of 8 respondents in a survey chose a particular option, 37.5% of the respondents selected that option. This percentage allows for easier interpretation and comparison of survey data.
-
Manufacturing Defects: If 3 out of 8 manufactured items are defective, the defect rate is 37.5%. This informs quality control measures and production adjustments.
-
Probability: In probability, 3 out of 8 represents the probability of a specific event occurring. This could be the probability of drawing a certain card from a deck or the probability of success in a trial. This understanding is crucial in many fields, including statistics and risk assessment.
-
Financial Analysis: Imagine analyzing investment performance. If 3 out of 8 investments showed a profit, this would represent a 37.5% success rate. This percentage could be used to assess the investment strategy's effectiveness.
Beyond the Percentage: Interpreting the Data
Simply stating that 3 out of 8 is 37.5% is only part of the story. The interpretation of this percentage is just as crucial as the calculation itself. Consider these points:
-
Context Matters: The significance of 37.5% depends heavily on the context. A 37.5% success rate in a high-stakes medical procedure would be viewed very differently than a 37.5% success rate in a simple game of chance.
-
Sample Size: The smaller the sample size (in this case, 8), the less reliable the percentage may be as a representation of the broader population. A larger sample would provide a more accurate and statistically significant result. For instance, 3 out of 8 may not be representative of the entire population but 300 out of 800 would be more robust.
-
Comparison: The percentage is most meaningful when compared to other percentages or to a benchmark. For example, a 37.5% success rate could be considered high, low, or average depending on the context and what's considered typical or expected.
Mathematical Extensions: Working with Proportions
Understanding the proportion 3:8 allows us to solve other related problems. For example:
-
Scaling Up: If 3 out of 8 items are defective, how many would be defective out of 16 items? We can set up a proportion: 3/8 = x/16. Solving for x, we find that 6 out of 16 items would be defective.
-
Scaling Down: If 3 out of 8 students passed an exam, how many would pass out of 4 students? The proportion becomes 3/8 = x/4. Solving for x, we find that 1.5 students would pass. Since we can't have half a student, we'd round this down to 1 student.
Frequently Asked Questions (FAQ)
Q: How do I calculate a percentage without a calculator?
A: You can perform the calculation using long division. Divide the numerator by the denominator, and then multiply the result by 100. For simple fractions, you can also use known fraction-to-percentage equivalents (e.g., 1/4 = 25%, 1/2 = 50%, 3/4 = 75%).
Q: What if I have a different ratio, such as 5 out of 12?
A: Follow the same steps: 5/12 = 0.4166... Multiply by 100 to get approximately 41.67%.
Q: Are there any online tools to calculate percentages?
A: Yes, many websites and apps offer free percentage calculators. These are helpful for quick calculations, but understanding the underlying principles is still essential.
Q: How can I improve my understanding of percentages and proportions?
A: Practice is key! Work through various problems with different ratios and percentages. Look for real-world examples to apply your knowledge.
Conclusion: Mastering Percentages and Proportions
Understanding "3 out of 8" goes far beyond simply calculating 37.5%. It's about grasping the fundamental concepts of ratios, proportions, and percentages. This understanding is crucial for interpreting data, solving problems, and making informed decisions in various aspects of life. By applying the principles outlined in this article, you can confidently tackle percentage calculations and enhance your understanding of proportional relationships. Remember that context and the size of the sample are important factors to consider when interpreting the results. Practice makes perfect – so continue to explore and apply these concepts to further solidify your understanding.
Latest Posts
Latest Posts
-
What Does Study Abroad Mean
Sep 19, 2025
-
90 Days From May 1
Sep 19, 2025
-
Where Is And Where Are
Sep 19, 2025
-
What Does Voulez Vous Mean
Sep 19, 2025
-
I Too Langston Hughes Analysis
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 3 Out Of 8 Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.