3 4 Cups X 4
scising
Sep 23, 2025 · 5 min read
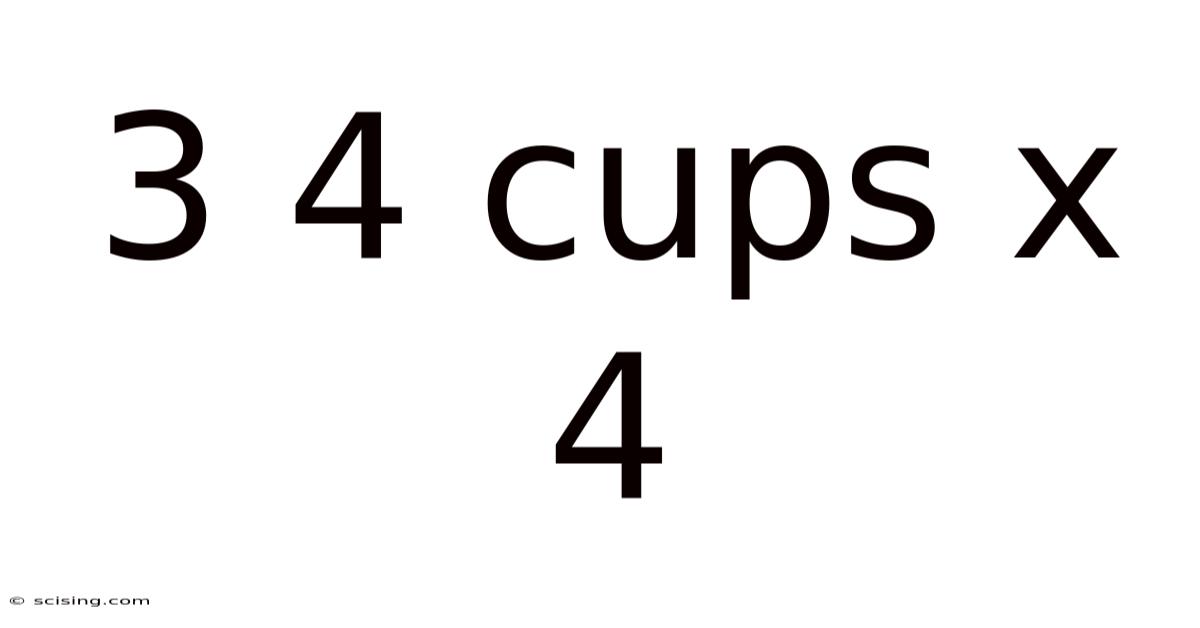
Table of Contents
Decoding 3, 4 Cups x 4: Exploring Variations and Applications in Mathematics and Beyond
This article delves into the multifaceted interpretations and applications of the expression "3, 4 cups x 4," exploring its mathematical meaning, potential ambiguities, and extensions into various fields. We'll unpack the core concept, address potential misunderstandings, and provide illustrative examples to enhance understanding. This exploration aims to clarify the expression's meaning and demonstrate its relevance beyond simple arithmetic.
Understanding the Core Concept: Mathematical Interpretation
At first glance, "3, 4 cups x 4" seems straightforward. However, the comma introduces an element of ambiguity. Mathematically, the expression lacks precise clarity. Let's consider the most probable interpretations:
Interpretation 1: Three separate instances of "4 cups x 4"
This interpretation treats the comma as a separator, indicating three distinct sets of calculations. In this case, we would have:
- Set 1: 4 cups x 4 = 16 cups
- Set 2: 4 cups x 4 = 16 cups
- Set 3: 4 cups x 4 = 16 cups
The overall result, under this interpretation, is a total of 16 cups + 16 cups + 16 cups = 48 cups. This approach is valid if the comma represents a list of independent operations, similar to listing items in a shopping list.
Interpretation 2: A combined quantity with a possible conversion factor
A different interpretation views "3, 4 cups" as a single quantity expressed in a non-standard format. The comma might represent a separator between whole numbers and fractions (although the fraction is missing a denominator). In this case, further information would be needed to provide a definite mathematical calculation. For example:
- If "3, 4 cups" represents 3.4 cups, then the calculation would be 3.4 cups x 4 = 13.6 cups. This would assume a decimal point is implicitly present.
- If "3, 4 cups" refers to a specific measurement unit not widely known, more context is needed to provide a valid answer. For instance, it might refer to a non-standard unit of volume specific to a certain region or industry.
Interpretation 3: A typographical error or a miscommunication
It's also possible that "3, 4 cups x 4" is a typographical error or a miscommunication. The comma's presence is highly unusual in standard mathematical notation concerning multiplication. A clearer expression would be "3 x 4 cups x 4" or "(3 + 4) cups x 4," which avoid ambiguity.
Expanding the Scope: Beyond Simple Arithmetic
While mathematical interpretations are important, the expression's ambiguity allows for exploration beyond pure numerical calculation. Let's consider some broader contexts:
1. Contextual Understanding: Culinary Applications
In a culinary context, "3, 4 cups x 4" could represent a recipe involving multiple batches or ingredients. Imagine a recipe calling for 3 ¼ cups (or 3.25 cups) of flour per batch, and the recipe requires 4 batches. In this scenario, the expression makes sense if we interpret "3, 4 cups" as 3.25 cups representing an approximation. The total flour required would be 3.25 cups/batch * 4 batches = 13 cups.
2. Data Representation: Possible Data Encoding
In data science or computer science, the expression could represent a form of data encoding. The comma might separate different data fields, while the 'x4' could indicate a scaling or repetition factor. For instance:
- '3' could represent a product ID.
- '4 cups' could represent a quantity or unit of measurement.
- 'x4' could indicate a replication factor (meaning 4 copies of the product with the specified quantity are needed).
This encoding would require a defined schema to decode the data accurately.
3. Ambiguity and the Importance of Precise Communication:
The expression highlights the critical importance of clear and unambiguous communication, especially in technical or quantitative contexts. Misinterpretations arising from ambiguous notation can lead to errors in calculations, recipes, data processing, and other scenarios. The principle of precise communication is crucial in many fields, from engineering and medicine to finance and software development.
Addressing Potential Questions (FAQ)
Q1: What is the most likely mathematical interpretation?
A1: The most likely, but not necessarily correct, mathematical interpretation depends heavily on context. If the comma is treated as a separator, the calculation becomes (4 cups x 4) x 3 = 48 cups. However, if "3, 4 cups" intends to represent a decimal number (3.4 cups), then the result is 3.4 cups x 4 = 13.6 cups. Ultimately, context is king.
Q2: How can I avoid similar ambiguities in my own writing?
A2: Use standard mathematical notation. Avoid using commas to represent decimal points or to separate different parts of a calculation unless you provide explicit instructions about how to interpret that comma. Always clearly define units of measurement. For complex expressions, use parentheses to group terms appropriately. If there's any uncertainty, clarify through additional explanations.
Q3: Could this expression be related to a specific mathematical concept?
A3: Not directly to a well-known mathematical concept. Its ambiguity prevents a direct association with a specific mathematical theorem or formula. However, it serves as a cautionary tale about the importance of clear notation and the potential for multiple interpretations of seemingly simple expressions.
Q4: Are there similar ambiguous expressions in other fields?
A4: Yes. Ambiguous expressions occur frequently in various domains. In natural language processing, understanding the meaning of sentences often relies on the context. In programming, incorrect punctuation or syntax can lead to errors. Ambiguity is a ubiquitous problem that requires meticulous attention to detail.
Conclusion: The Value of Clarity and Precision
The seemingly simple expression "3, 4 cups x 4" underscores the critical role of clear communication in any field involving quantitative data. Its ambiguity reveals the importance of consistent notation, appropriate use of mathematical symbols, and careful attention to context. Avoiding ambiguous expressions through precise language and standard notation is crucial for accurate interpretation and successful outcomes in various fields, preventing misunderstandings and errors. This analysis not only solves the initial problem but also provides a broader lesson on the importance of clarity and precision in communication, a skill transferable to numerous academic and professional endeavors. The seemingly simple "3, 4 cups x 4" becomes a powerful illustration of how seemingly simple expressions can lead to multiple interpretations, highlighting the need for clear and unambiguous communication.
Latest Posts
Latest Posts
-
How Much Is 600 Milliliters
Sep 23, 2025
-
Barar And Abdollahi Cell Model
Sep 23, 2025
-
How Much Is 3 L
Sep 23, 2025
-
Salir In The Present Tense
Sep 23, 2025
-
4 000 Pounds To Tons
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 3 4 Cups X 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.