3 000 Divided By 12
scising
Sep 23, 2025 · 6 min read
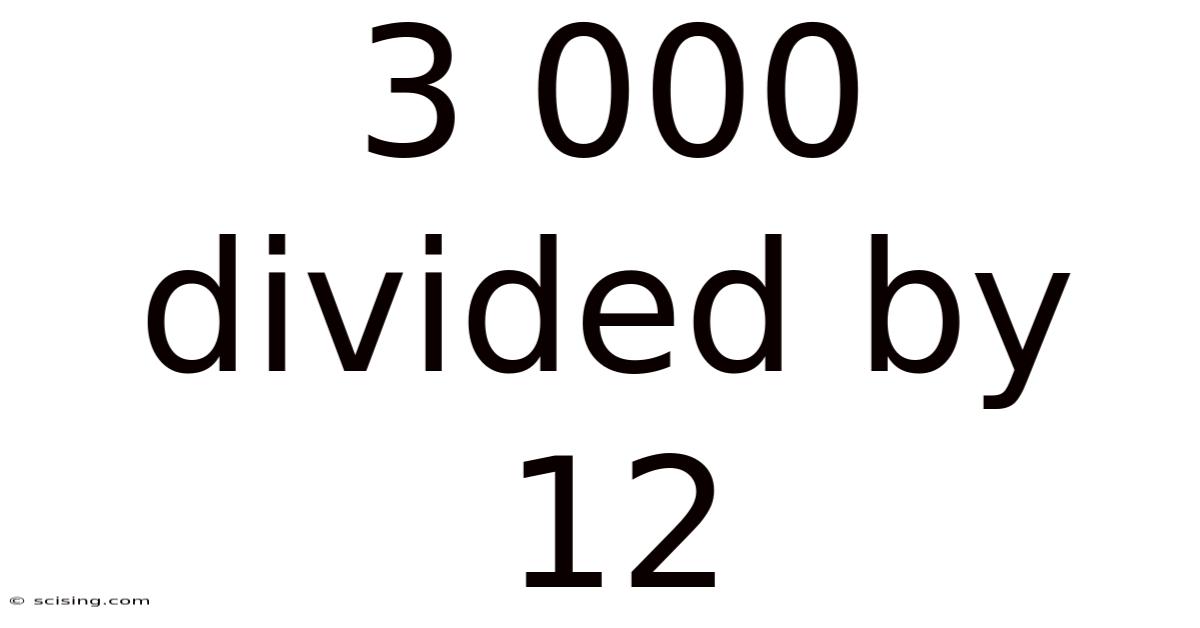
Table of Contents
Unveiling the Mystery: 3000 Divided by 12 – A Deep Dive into Division
This article explores the seemingly simple mathematical problem of 3000 divided by 12, going beyond the basic answer to delve into the underlying principles, practical applications, and related concepts. Understanding division is fundamental to various aspects of life, from everyday budgeting to complex scientific calculations. We'll unpack this specific problem to illuminate broader mathematical understanding and build your confidence in tackling similar challenges.
Introduction: The Fundamentals of Division
Division is one of the four basic arithmetic operations, alongside addition, subtraction, and multiplication. It essentially involves splitting a quantity into equal parts. In the problem 3000 ÷ 12, we are asking: "How many times does 12 fit into 3000?" The answer provides the number of equal groups of 12 we can create from a total of 3000.
This seemingly straightforward question has far-reaching implications across numerous fields. From evenly distributing resources in a classroom to calculating unit costs in business, understanding division is crucial for effective problem-solving. This exploration will not only provide the solution but also illuminate the various methods for calculating it, enriching your mathematical intuition.
Method 1: Long Division – A Step-by-Step Approach
Long division is a classical method for solving division problems, particularly those involving larger numbers. Let's break down the process for 3000 ÷ 12:
-
Set up the problem: Write the dividend (3000) inside the long division symbol (⟌) and the divisor (12) outside.
12⟌3000 -
Divide the first digit(s): 12 doesn't go into 3, so we consider the first two digits: 30. 12 goes into 30 twice (12 x 2 = 24). Write the '2' above the '0' in 3000.
2 12⟌3000 -
Multiply and subtract: Multiply the quotient (2) by the divisor (12): 2 x 12 = 24. Subtract this result from the first two digits of the dividend: 30 - 24 = 6.
2 12⟌3000 24 --- 6 -
Bring down the next digit: Bring down the next digit from the dividend (0) to create the number 60.
2 12⟌3000 24 --- 60 -
Repeat the process: 12 goes into 60 five times (12 x 5 = 60). Write the '5' above the next '0' in 3000.
25 12⟌3000 24 --- 60 60 --- 0 -
Multiply and subtract: Multiply the new quotient digit (5) by the divisor (12): 5 x 12 = 60. Subtract this from 60: 60 - 60 = 0.
-
Bring down the last digit: Bring down the last digit (0) from the dividend. Since we have a remainder of 0, 12 goes into 0 zero times.
250 12⟌3000 24 --- 60 60 --- 00 00 --- 0
Therefore, 3000 ÷ 12 = 250.
Method 2: Using Multiplication – The Inverse Operation
Division and multiplication are inverse operations. This means that if we multiply the quotient by the divisor, we should get the dividend. We can use this relationship to check our answer or even to solve the problem in a different way.
We are looking for a number that, when multiplied by 12, equals 3000. We can estimate this by using our knowledge of multiplication tables and working our way up. Knowing that 12 x 100 = 1200 and 12 x 200 = 2400, we can deduce that the answer is likely somewhere around 250. A quick multiplication confirms: 12 x 250 = 3000.
Method 3: Breaking Down the Problem – Simplifying the Calculation
We can simplify the problem by breaking it down into smaller, more manageable parts. Since 3000 is divisible by 10, let's start with that:
- 3000 ÷ 10 = 300
Now we have 300 ÷ 1.2 (since 12 is 1.2 x 10). This can further be simplified:
- 300 ÷ 1.2 = 3000 ÷ 12 This is our original problem!
However, we can manipulate it differently:
- 300 ÷ 12 = 25. (You can use long division to find this easily)
Since we initially divided by 10, we should multiply this result by 10:
- 25 x 10 = 250
Again, we arrive at the solution: 3000 ÷ 12 = 250. This approach highlights the flexibility in applying mathematical principles.
Real-World Applications: Where Division Matters
The seemingly simple calculation of 3000 ÷ 12 has practical applications in numerous real-world scenarios:
-
Budgeting: Imagine you have a yearly budget of $3000 and you want to allocate it equally across 12 months. Dividing 3000 by 12 gives you a monthly budget of $250.
-
Resource Allocation: A teacher has 3000 pencils to distribute evenly among 12 classrooms. Each classroom receives 250 pencils.
-
Unit Cost: A company purchased 3000 units of a product for $12,000. The unit cost is found by dividing 12000 by 3000. Conversely, if they want to sell them for $12 each, they can find how many units are required to reach $3000 in revenue by dividing 3000 by 12. The answer is 250 units.
-
Scientific Calculations: Many scientific formulas and calculations involve division, from calculating average speeds to determining concentrations.
Understanding Remainders: When Division Isn't Exact
While 3000 is perfectly divisible by 12, let's consider what happens when the division doesn't result in a whole number. For example, 3005 ÷ 12. Using long division:
- 12 goes into 30 twice (24).
- 30 - 24 = 6.
- Bring down the 0: 60.
- 12 goes into 60 five times (60).
- Bring down the 5: 5.
- 12 does not go into 5. The remainder is 5.
The result is 250 with a remainder of 5. This means that 3005 can be divided into 250 groups of 12, with 5 left over. Remainders are important in various applications, highlighting incomplete divisions or leftover quantities.
Expanding Your Mathematical Horizons: Further Exploration
Understanding division, as demonstrated through 3000 ÷ 12, paves the way for more advanced mathematical concepts. Exploring these concepts will further enhance your problem-solving capabilities:
-
Fractions and Decimals: Division is intrinsically linked to fractions and decimals. 3000 ÷ 12 can be expressed as the fraction 3000/12, which simplifies to 250/1.
-
Algebra: Algebraic equations often involve division, requiring you to isolate variables through division.
-
Calculus: Calculus, the study of change, relies heavily on the fundamental principles of arithmetic, including division, to analyze rates of change and other dynamic phenomena.
-
Advanced Arithmetic: Understanding Prime Numbers and factorization, greatest common divisors (GCD), and least common multiples (LCM) are further developments of core mathematical principles, including division.
Frequently Asked Questions (FAQ)
-
Q: What is the easiest way to solve 3000 divided by 12?
A: The easiest way depends on your individual comfort level. For many, using a calculator is quickest. However, understanding the long division method provides a deeper understanding of the process.
-
Q: What if I get a different answer?
A: Double-check your calculations. Make sure you're following the steps correctly in long division or using the correct method in your chosen approach.
-
Q: Are there any shortcuts for solving division problems like this?
A: Yes! Recognizing divisibility rules and breaking down the problem into simpler parts, as shown above, can often lead to efficient solutions.
-
Q: Why is understanding division important?
A: Division is a fundamental arithmetic operation used in countless daily activities and advanced mathematical concepts, making it crucial for problem-solving across various fields.
Conclusion: Mastering Division – One Step at a Time
Solving 3000 divided by 12 is more than just finding the answer (250). It's about understanding the underlying principles of division and appreciating its significance in mathematics and everyday life. By exploring different methods and applications, we've deepened our understanding of this fundamental operation and expanded our mathematical toolkit. Remember, consistent practice and a curious mind are key to mastering mathematical concepts and building a strong foundation for future learning. So, continue to explore, experiment, and embrace the beauty of mathematics!
Latest Posts
Latest Posts
-
Pic Of A Real Dragon
Sep 23, 2025
-
What Is 0 Times X
Sep 23, 2025
-
Lewis Dot Structure Of K
Sep 23, 2025
-
1 4 Of A Pound
Sep 23, 2025
-
What Country Is Near Japan
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 3 000 Divided By 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.