25 Percent To A Decimal
scising
Sep 13, 2025 · 5 min read
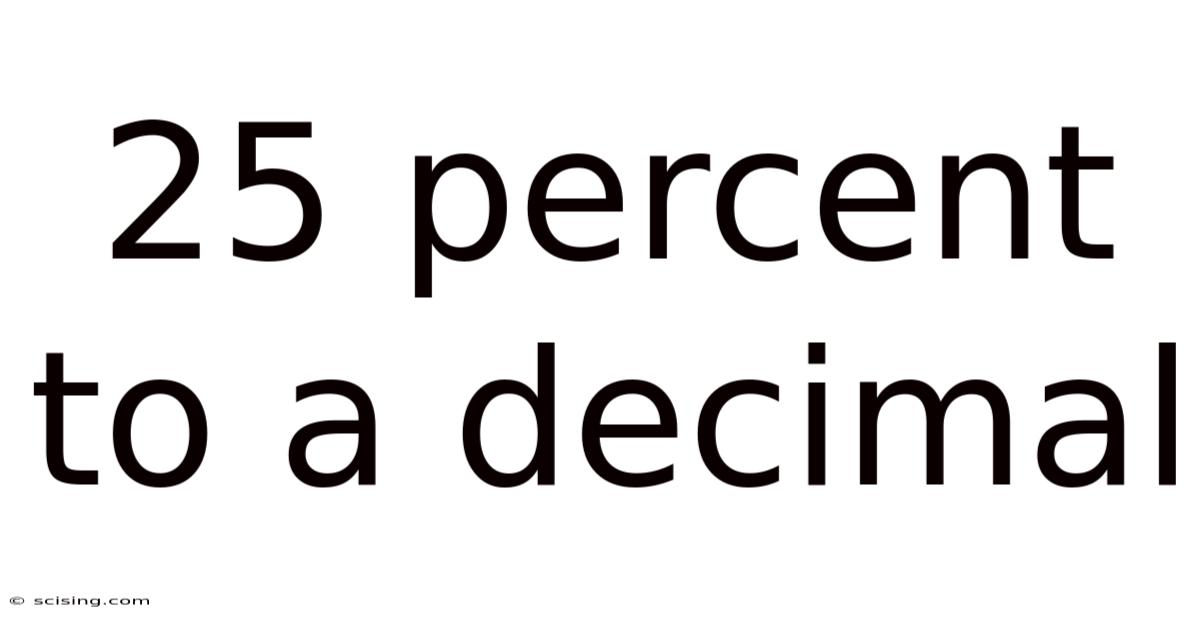
Table of Contents
Converting 25 Percent to a Decimal: A Comprehensive Guide
Understanding how to convert percentages to decimals is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced scientific analyses. This comprehensive guide will delve into the process of converting 25 percent to a decimal, providing a step-by-step explanation, exploring the underlying principles, and offering practical examples to solidify your understanding. We'll also examine the broader context of percentage-to-decimal conversions and answer frequently asked questions.
Understanding Percentages and Decimals
Before diving into the conversion, let's clarify the concepts of percentages and decimals. A percentage represents a fraction of 100. The word "percent" literally means "out of one hundred" ( per cent). For example, 25% means 25 out of 100. A decimal, on the other hand, is a way of expressing a number using base-10, where the digits to the right of the decimal point represent fractions of powers of 10 (tenths, hundredths, thousandths, etc.).
The relationship between percentages and decimals is direct: a percentage can always be expressed as a decimal, and vice-versa. This interchangeability makes them powerful tools for representing proportions and fractions in various contexts.
Converting 25 Percent to a Decimal: The Method
Converting 25% to a decimal involves a straightforward process:
-
Divide by 100: The core principle is that a percentage is a fraction with a denominator of 100. To convert a percentage to a decimal, you simply divide the percentage value by 100.
-
Calculation: In this case, we have 25%. Dividing 25 by 100 gives us: 25 ÷ 100 = 0.25
Therefore, 25% expressed as a decimal is 0.25.
Visualizing the Conversion
Imagine a pie chart representing a whole (100%). If you divide the pie into four equal slices, each slice represents 25% of the whole. Each slice also represents 0.25 of the whole pie. This visual representation helps solidify the connection between the percentage and its decimal equivalent.
Practical Applications of Percentage-to-Decimal Conversion
The ability to convert percentages to decimals is invaluable in numerous real-world situations:
-
Finance: Calculating interest rates, discounts, tax rates, and profit margins often require converting percentages to decimals. For example, calculating a 25% discount on a $100 item involves multiplying $100 by 0.25 ($100 * 0.25 = $25).
-
Science: Many scientific calculations involve percentages, such as expressing experimental error or representing the concentration of a solution. Converting to decimals simplifies calculations and facilitates data analysis.
-
Statistics: Percentages are frequently used to represent data in statistical analyses. Converting them to decimals is necessary for statistical calculations and interpretations.
-
Everyday Life: Understanding percentages and decimals helps in situations like calculating tips, comparing prices, or understanding sale promotions.
Beyond 25%: Converting Other Percentages to Decimals
The method outlined above applies to converting any percentage to a decimal. Let's consider a few more examples:
- 50%: 50 ÷ 100 = 0.50
- 75%: 75 ÷ 100 = 0.75
- 10%: 10 ÷ 100 = 0.10
- 1%: 1 ÷ 100 = 0.01
- 125%: 125 ÷ 100 = 1.25 (Note: Percentages greater than 100% result in decimals greater than 1)
Converting Decimals to Percentages
The reverse process—converting a decimal to a percentage—is equally important. To do this, simply multiply the decimal by 100 and add a "%" sign.
For example:
- 0.75 * 100 = 75%
- 0.10 * 100 = 10%
- 1.50 * 100 = 150%
The Importance of Place Value in Decimal Conversions
Understanding place value is crucial for accurate decimal conversions. Each digit in a decimal number holds a specific value based on its position relative to the decimal point. For instance, in the decimal 0.25, the '2' represents two tenths (2/10), and the '5' represents five hundredths (5/100).
Working with Fractions and Percentages
Often, you'll need to convert fractions to percentages and decimals. This involves two steps:
- Convert the fraction to a decimal: Divide the numerator by the denominator.
- Convert the decimal to a percentage: Multiply the decimal by 100 and add a "%" sign.
For example, let's convert the fraction 1/4 to a percentage and a decimal:
- Decimal: 1 ÷ 4 = 0.25
- Percentage: 0.25 * 100 = 25%
This demonstrates the interconnectedness of fractions, decimals, and percentages.
Using Calculators for Conversions
While the manual method is valuable for understanding the underlying principles, calculators can significantly speed up the conversion process, especially when dealing with more complex percentages or large numbers. Most calculators have a percentage function (%) that simplifies the conversion directly.
Frequently Asked Questions (FAQ)
Q: Can I convert percentages with decimal places?
A: Absolutely! The same principle applies. For example, to convert 25.5% to a decimal, divide 25.5 by 100: 25.5 ÷ 100 = 0.255.
Q: What about negative percentages?
A: Negative percentages are handled similarly. For example, -25% becomes -0.25 when converted to a decimal. This often represents a decrease or loss.
Q: How do I convert a percentage to a fraction?
A: First, convert the percentage to a decimal. Then, express the decimal as a fraction by placing the decimal value over 1 and simplifying the fraction. For example, 25% = 0.25 = 25/100 = 1/4.
Q: Are there any shortcuts for converting common percentages?
A: Yes! For example, recognizing that 50% is 1/2 and 25% is 1/4 can simplify mental calculations.
Conclusion
Converting 25 percent to a decimal, and more broadly, understanding the interplay between percentages and decimals, is an essential mathematical skill with widespread applications. This guide has detailed the process, provided practical examples, and explored related concepts to equip you with a comprehensive understanding. Mastering this conversion will enhance your problem-solving abilities across various fields, from everyday budgeting to advanced scientific research. Remember the fundamental principle: divide by 100 to convert a percentage to a decimal, and multiply by 100 to perform the reverse operation. Practice consistently to solidify your understanding and build confidence in handling these fundamental mathematical concepts.
Latest Posts
Latest Posts
-
Storage Area Of A Cell
Sep 13, 2025
-
36 5 C To F
Sep 13, 2025
-
Why Are Halogens So Reactive
Sep 13, 2025
-
Parietal Lobe Ap Psychology Definition
Sep 13, 2025
-
Latin Root Word For Light
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 25 Percent To A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.