20 Percent Of 1.3 Meters
scising
Sep 24, 2025 · 6 min read
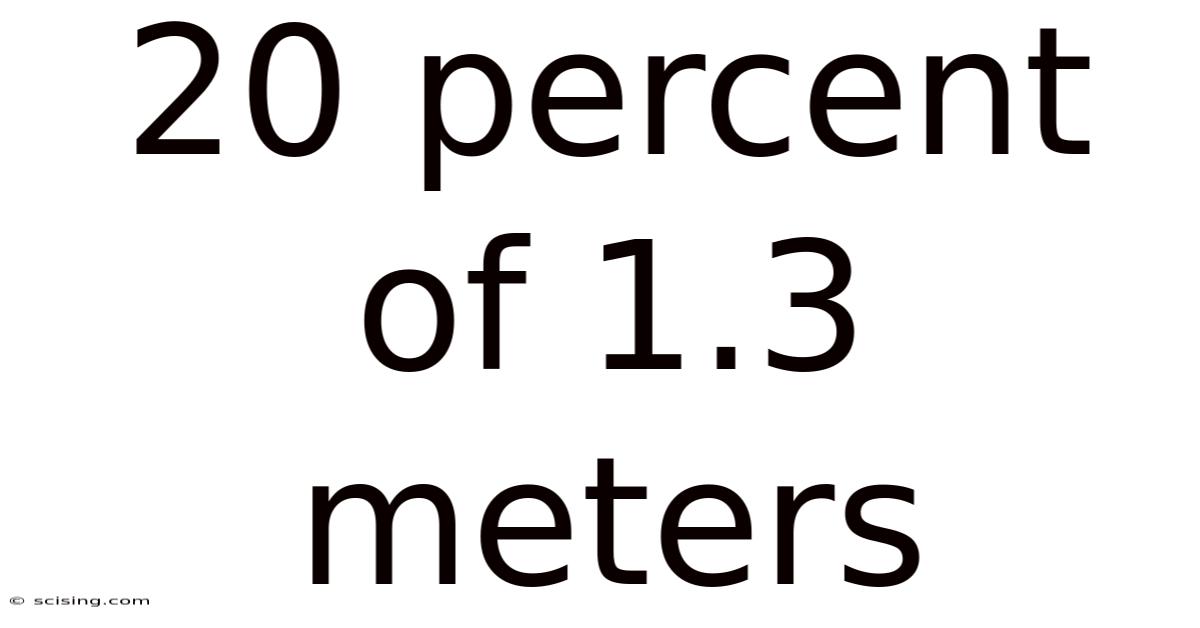
Table of Contents
Decoding 20% of 1.3 Meters: A Deep Dive into Percentages and Measurement
Finding 20% of 1.3 meters might seem like a simple calculation, a quick task for a calculator. However, this seemingly straightforward problem opens the door to understanding fundamental concepts in mathematics, particularly percentages and unit conversions, applicable across numerous fields from everyday life to advanced scientific calculations. This article will not only solve the problem but also delve into the underlying principles, exploring different approaches, practical applications, and addressing potential misconceptions.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent" or "out of 100". For instance, 20% means 20 out of 100, which can be written as the fraction 20/100 or the decimal 0.20. Understanding this fundamental definition is crucial for tackling percentage calculations.
Method 1: Direct Calculation
The most straightforward method to calculate 20% of 1.3 meters is to convert the percentage to a decimal and then multiply it by the given value.
- Step 1: Convert the percentage to a decimal: 20% = 20/100 = 0.20
- Step 2: Multiply the decimal by the value: 0.20 * 1.3 meters = 0.26 meters
Therefore, 20% of 1.3 meters is 0.26 meters.
Method 2: Fractional Approach
Alternatively, we can use the fractional representation of the percentage.
- Step 1: Express the percentage as a fraction: 20% = 20/100 = 1/5
- Step 2: Multiply the fraction by the value: (1/5) * 1.3 meters = 1.3 meters / 5 = 0.26 meters
This method reinforces the understanding that percentages are simply fractions with a denominator of 100. Both methods yield the same result: 0.26 meters.
Understanding Units: Meters and Centimeters
The result of our calculation, 0.26 meters, is a metric unit of length. While this is perfectly acceptable, it’s often beneficial to express the answer in different units depending on the context. Converting 0.26 meters to centimeters can provide a clearer picture, especially in practical scenarios.
Since there are 100 centimeters in 1 meter, we can convert 0.26 meters to centimeters by multiplying by 100:
0.26 meters * 100 centimeters/meter = 26 centimeters
Therefore, 20% of 1.3 meters is equivalent to 26 centimeters.
Practical Applications
The calculation of percentages is widely used in various real-world situations. Here are a few examples where this particular calculation (20% of 1.3 meters) might be relevant:
-
Construction and Engineering: Calculating material requirements. If a construction project needs 1.3 meters of a specific pipe and only 20% is needed for a particular section, then 0.26 meters (or 26 centimeters) would be the required length.
-
Textiles and Tailoring: Determining fabric requirements. If a tailor needs 1.3 meters of fabric for a garment and only 20% of it is used for a specific part, then 0.26 meters (or 26 centimeters) is the amount needed.
-
Gardening and Landscaping: Calculating plant spacing or material quantities. If a gardener needs 1.3 meters of a particular type of plant for a flower bed and only 20% is required for a specific section, then 0.26 meters will be the portion needed.
-
Cooking and Baking: Scaling recipes. If a recipe calls for 1.3 meters of pastry dough, and you only want to make 20% of the recipe, you would use 0.26 meters. (While less common, this example illustrates the broad applicability of percentage calculations).
Advanced Concepts and Extensions
While the initial problem was simple, let's explore some related concepts that build upon the foundational understanding we've established:
-
Calculating other percentages: The methods described can be easily adapted to calculate any percentage of 1.3 meters (or any other value). Simply replace 0.20 (or 1/5) with the decimal or fractional equivalent of the desired percentage.
-
Finding the original value: If you know that 26 centimeters represents 20% of a certain length, you can work backward to find the original length. This involves dividing the known value (26 centimeters) by the percentage (0.20) to obtain the original value of 130 centimeters (or 1.3 meters).
-
Compound Percentages: In more complex scenarios, you might need to calculate multiple percentages sequentially. For example, you might need to calculate a 20% discount on an item and then add a 10% tax. This involves multiple percentage calculations, building upon the initial result.
-
Percentage Change: This involves determining the percentage difference between two values. For instance, if the length increased from 1.3 meters to 1.5 meters, calculating the percentage change would require identifying the difference (0.2 meters), dividing it by the original value (1.3 meters), and then multiplying by 100% to express it as a percentage.
Addressing Common Misconceptions
Several common misconceptions surround percentage calculations:
-
Adding percentages directly: A common mistake is to add percentages directly without considering their base values. For example, a 20% increase followed by a 20% decrease does not result in the original value. The second 20% decrease is applied to the new value after the initial increase, leading to a net decrease.
-
Ignoring units: Always pay attention to units. Ignoring units can lead to incorrect calculations and misinterpretations. In our example, consistently using meters (or centimeters) is crucial for accurate results.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to solve this? A: Absolutely! Calculators are efficient tools for percentage calculations. Simply input 0.20 * 1.3 and the calculator will give you the answer.
-
Q: What if the value wasn't 1.3 meters, but a different number? A: The methods described remain the same. Simply replace 1.3 meters with the new value and perform the calculations using the chosen method (decimal or fraction).
-
Q: Why is it important to understand both decimal and fractional representations of percentages? A: Understanding both representations provides a more comprehensive grasp of percentages. Using fractions can sometimes simplify calculations, while decimals are often more convenient for calculator use. Both approaches enhance problem-solving flexibility.
-
Q: Are there any online tools or software that can help with percentage calculations? A: Yes, many online calculators and software programs are available to assist with percentage calculations. These tools can automate the process and reduce the risk of manual errors. However, understanding the underlying concepts remains essential.
Conclusion
Calculating 20% of 1.3 meters, while seemingly simple, provides a valuable opportunity to reinforce our understanding of percentages, unit conversions, and their practical applications across various fields. Mastering these fundamental concepts is essential for success in numerous academic and professional endeavors. The methods presented – both the direct decimal multiplication and the fractional approach – offer flexibility and enhance comprehension. Remember to always consider the units and avoid common misconceptions to ensure accurate and meaningful results. This detailed explanation goes beyond a simple numerical answer; it offers a comprehensive exploration of the underlying mathematical principles and their practical relevance, encouraging deeper understanding and problem-solving skills.
Latest Posts
Latest Posts
-
Use Retribution In A Sentence
Sep 24, 2025
-
Group Of Chicken Is Called
Sep 24, 2025
-
Act Two The Crucible Summary
Sep 24, 2025
-
75 Days From August 1
Sep 24, 2025
-
What Is A Saturated Hydrocarbon
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 20 Percent Of 1.3 Meters . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.