2.5 Percent As A Decimal
scising
Sep 12, 2025 · 5 min read
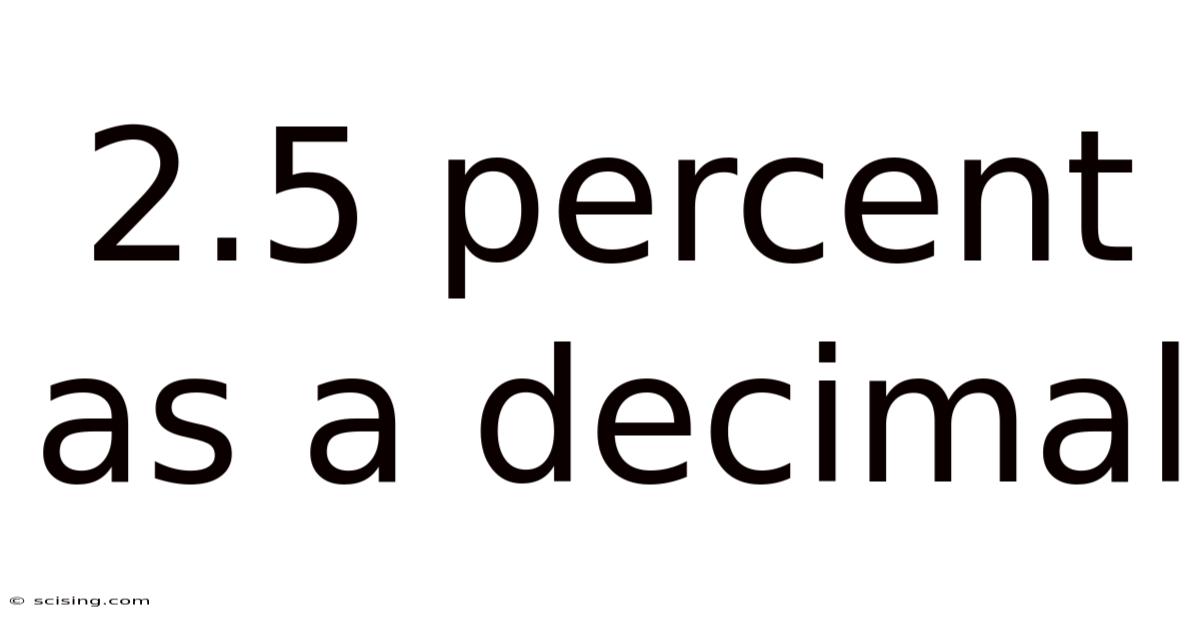
Table of Contents
2.5 Percent as a Decimal: A Comprehensive Guide
Understanding percentages and their decimal equivalents is a fundamental skill in mathematics and essential for various applications in everyday life, from calculating discounts and taxes to understanding financial reports and statistical data. This comprehensive guide will delve into the conversion of 2.5 percent to its decimal form, explaining the process in detail and providing further insights into the broader concept of percentage-to-decimal conversions. We'll explore the underlying principles, offer practical examples, and address frequently asked questions. By the end, you'll not only know the answer but also understand the "why" behind the conversion.
Understanding Percentages and Decimals
Before diving into the specific conversion of 2.5 percent, let's establish a firm understanding of the relationship between percentages and decimals. A percentage represents a fraction of 100. The symbol "%" signifies "per hundred" or "out of 100." For example, 50% means 50 out of 100, which can be written as the fraction 50/100 or the decimal 0.50.
A decimal, on the other hand, is a way of expressing numbers that are not whole numbers. Decimals use a base-ten system, where numbers to the right of the decimal point represent fractions of powers of ten (tenths, hundredths, thousandths, and so on).
The key relationship to remember is that percentages are simply decimals multiplied by 100. Therefore, converting between percentages and decimals involves a simple multiplication or division by 100.
Converting 2.5 Percent to a Decimal
To convert 2.5 percent to a decimal, we follow these steps:
-
Remove the Percent Symbol: The first step is to remove the "%" symbol from 2.5%. This leaves us with the number 2.5.
-
Divide by 100: The next, and crucial, step is to divide the number by 100. This is because a percentage represents a fraction of 100. Therefore, dividing by 100 converts the percentage to its decimal equivalent. 2.5 divided by 100 is 0.025.
Therefore, 2.5% as a decimal is 0.025.
This simple process can be expressed as a formula:
Decimal = Percentage / 100
In this case:
Decimal = 2.5 / 100 = 0.025
Practical Applications of 2.5% as a Decimal
Understanding the decimal equivalent of 2.5% is crucial in various real-world scenarios. Here are a few examples:
-
Financial Calculations: If a bank offers an interest rate of 2.5% on a savings account, knowing that this is equivalent to 0.025 allows for easier calculation of the interest earned. For example, on a balance of $1000, the interest earned would be $1000 * 0.025 = $25.
-
Discount Calculations: If an item is discounted by 2.5%, you can quickly calculate the discount amount by multiplying the original price by 0.025. For example, on a $50 item, the discount would be $50 * 0.025 = $1.25.
-
Statistical Analysis: In statistical analysis, percentages are often converted to decimals for calculations involving probabilities, proportions, and other statistical measures.
-
Scientific Calculations: Many scientific formulas require using decimal values, and understanding percentage-to-decimal conversions is essential for accurate calculations.
Converting Decimals to Percentages: The Reverse Process
While we've focused on converting 2.5% to a decimal, it's equally important to understand the reverse process: converting a decimal to a percentage. This involves multiplying the decimal by 100 and adding the "%" symbol.
For example, let's convert 0.025 back to a percentage:
-
Multiply by 100: 0.025 * 100 = 2.5
-
Add the Percent Symbol: 2.5%
This process can be expressed as a formula:
Percentage = Decimal * 100
Working with Percentages Greater Than 100%
It's also important to note that percentages can be greater than 100%. This simply means that the value represents more than the whole. The conversion process remains the same. For example:
- 150% as a decimal is 150/100 = 1.5
- 200% as a decimal is 200/100 = 2
Understanding the Place Value System in Decimals
The conversion from 2.5% to 0.025 highlights the importance of understanding the place value system in decimals. The digit '2' in 0.025 represents two hundredths (2/100), and the digit '5' represents five thousandths (5/1000). A thorough understanding of place value is crucial for accurate decimal manipulation and calculations.
Frequently Asked Questions (FAQ)
Q: Why do we divide by 100 when converting a percentage to a decimal?
A: We divide by 100 because a percentage is a fraction of 100. Dividing by 100 essentially converts the percentage from "parts per hundred" to a decimal representation.
Q: Can I convert percentages with decimals (like 2.5%) directly using a calculator?
A: Yes, most calculators can handle this directly. Simply enter "2.5 / 100" and the calculator will provide the decimal equivalent (0.025).
Q: What if the percentage is a whole number (e.g., 10%)?
A: The process remains the same. 10% is equal to 10/100 = 0.10.
Q: Are there any other methods to convert percentages to decimals besides division by 100?
A: While division by 100 is the most straightforward method, you can also think of it as moving the decimal point two places to the left. For example, in 2.5%, moving the decimal point two places to the left gives you 0.025.
Q: Why is understanding percentage-to-decimal conversion important?
A: This conversion is fundamental to various fields, including finance, statistics, science, and everyday life. Accurate conversions ensure correct calculations in areas like interest, discounts, taxes, and many other applications.
Conclusion
Converting 2.5 percent to its decimal equivalent (0.025) is a straightforward process involving a simple division by 100. This conversion is a vital skill with broad applications across numerous disciplines. Understanding the underlying principles of percentages and decimals, along with the ability to perform these conversions accurately, is crucial for both mathematical proficiency and practical problem-solving in various real-world contexts. Mastering this concept provides a solid foundation for more advanced mathematical and financial applications. Remember to practice regularly to solidify your understanding and build confidence in handling these calculations effortlessly.
Latest Posts
Latest Posts
-
8 5 Divided By 3
Sep 12, 2025
-
What Does Tare Weight Mean
Sep 12, 2025
-
Is A Rectangle A Trapezoid
Sep 12, 2025
-
Evidence Of A Chemical Reaction
Sep 12, 2025
-
Cradle To The Grave Book
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 2.5 Percent As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.