15 Percent In Decimal Form
scising
Sep 12, 2025 · 5 min read
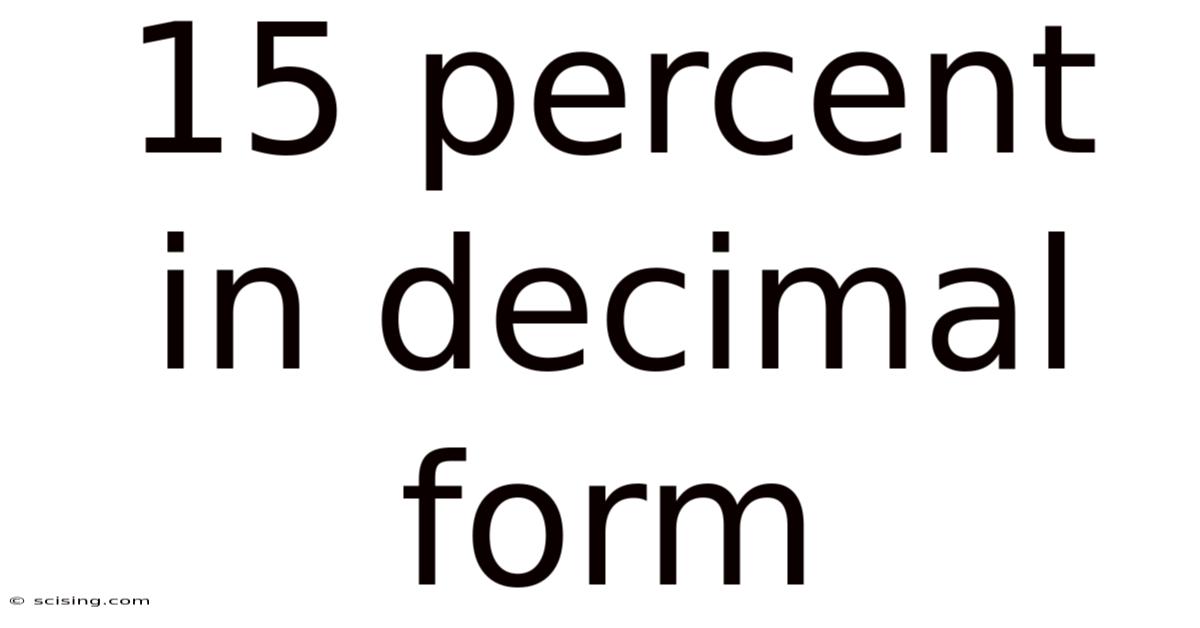
Table of Contents
15 Percent in Decimal Form: A Comprehensive Guide
Understanding percentages is a fundamental skill in various aspects of life, from calculating discounts at the mall to analyzing financial reports. This article will delve deep into the conversion of percentages to decimals, focusing specifically on how to represent 15 percent in decimal form. We'll explore the underlying mathematical principles, provide practical examples, and address common questions, ensuring a comprehensive understanding of this seemingly simple yet crucial concept.
Introduction: Understanding Percentages and Decimals
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred" (per cent). Therefore, 15 percent (15%) means 15 out of 100. Decimals, on the other hand, are a way of representing numbers using a base-ten system, where the position of a digit determines its value. Converting between percentages and decimals is a straightforward process involving simple arithmetic.
Converting Percentages to Decimals: The Basic Method
The fundamental principle behind converting a percentage to a decimal is dividing the percentage by 100. This is because a percentage is always a fraction of 100. For 15 percent, the conversion is:
15% = 15 ÷ 100 = 0.15
Therefore, 15 percent in decimal form is 0.15. This method applies to any percentage; simply divide the numerical part of the percentage by 100.
The Shortcut: Moving the Decimal Point
A quicker way to convert a percentage to a decimal is by moving the decimal point two places to the left. This is equivalent to dividing by 100. Since 15% is understood to be 15.0%, moving the decimal point two places to the left gives us 0.15. This shortcut is particularly useful for quick mental calculations.
Visualizing the Conversion: A Fraction Approach
Understanding the conversion can be enhanced by visualizing it using fractions. 15% can be written as the fraction 15/100. To convert this fraction to a decimal, we divide the numerator (15) by the denominator (100):
15 ÷ 100 = 0.15
This reinforces the concept that a percentage is simply a fraction with a denominator of 100.
Practical Applications of 15% in Decimal Form
The decimal form of 15%, 0.15, has numerous applications in various fields:
-
Finance: Calculating interest rates, discounts, and tax amounts often involves using decimal representations of percentages. For example, a 15% discount on a $100 item would be calculated as 0.15 * $100 = $15.
-
Statistics: Representing proportions and probabilities in statistical analysis commonly uses decimals. A 15% chance of an event occurring is represented as 0.15.
-
Science: Many scientific calculations and data representations involve decimal forms of percentages. For example, expressing the concentration of a solution or the percentage change in a measurement.
-
Everyday Life: Calculating tips in restaurants, determining sale prices, and understanding growth rates are all situations where understanding 0.15 as the decimal equivalent of 15% is beneficial.
Advanced Concepts: Percentages Greater Than 100%
While the examples above focus on percentages less than 100%, the conversion method remains the same for percentages greater than 100%. For instance, 115% in decimal form is:
115% = 115 ÷ 100 = 1.15
This represents a value greater than 1, indicating a quantity exceeding the original whole. This is common when discussing growth rates or increases in value.
Converting Decimals to Percentages: The Reverse Process
Just as we convert percentages to decimals, we can perform the reverse process. To convert a decimal to a percentage, simply multiply the decimal by 100 and add the % symbol. For example, to convert 0.15 back to a percentage:
0.15 * 100 = 15%
This demonstrates the reversible nature of the conversion between percentages and decimals.
Understanding the Significance of Place Value
The conversion process hinges on the understanding of place value in the decimal system. When we divide by 100, we effectively move the decimal point two places to the left. This shifts the digits to represent smaller fractional values. Conversely, multiplying by 100 moves the decimal point two places to the right, representing larger values.
Illustrative Examples: Real-World Scenarios
Let's look at a few practical examples demonstrating the application of 15% in its decimal form:
Example 1: Sales Tax: Suppose the sales tax in your region is 15%. If you buy an item costing $50, the sales tax would be:
0.15 * $50 = $7.50
Example 2: Discount: A store offers a 15% discount on all items. If an item is priced at $200, the discount amount is:
0.15 * $200 = $30
Example 3: Interest: You deposit $1000 in a savings account with a 15% annual interest rate. The interest earned after one year would be:
0.15 * $1000 = $150
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to convert percentages to decimals?
A: Yes, absolutely! Most calculators have a percentage function (%) that simplifies the conversion. However, understanding the manual method is crucial for comprehending the underlying mathematical principles.
Q: What if the percentage has a decimal itself (e.g., 15.5%)?
A: The process remains the same. Divide the percentage by 100. 15.5% becomes 15.5 ÷ 100 = 0.155.
Q: Why is understanding this conversion important?
A: This conversion is fundamental in various fields, enabling accurate calculations in finance, statistics, science, and daily life. It's a foundational skill for many more advanced mathematical concepts.
Q: Are there any other ways to represent 15%?
A: Yes, 15% can also be represented as a fraction (15/100), which can be simplified to 3/20. All three representations – percentage, decimal, and fraction – are equivalent ways of expressing the same value.
Conclusion: Mastering the Conversion of Percentages to Decimals
Understanding how to represent 15 percent in decimal form (0.15) is a fundamental skill with widespread applications. This article has explored the process, provided illustrative examples, and addressed common questions. Mastering this conversion not only aids in solving everyday problems but also lays a solid foundation for more advanced mathematical and statistical concepts. By grasping the underlying principles of percentages and decimals, you'll enhance your problem-solving abilities and navigate numerical challenges with greater confidence and efficiency. Remember, practice is key to solidifying your understanding of this important mathematical concept. Regular practice with various percentage values will help you internalize the conversion process and apply it effortlessly in any situation.
Latest Posts
Latest Posts
-
Whats 20 Percent Of 1000
Sep 12, 2025
-
Body Parts Starts With D
Sep 12, 2025
-
3 Percent Of 1 Million
Sep 12, 2025
-
Pros And Cons Of Technology
Sep 12, 2025
-
Lion Costume Wizard Of Oz
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 15 Percent In Decimal Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.