12 Is What Of 60
scising
Sep 07, 2025 · 5 min read
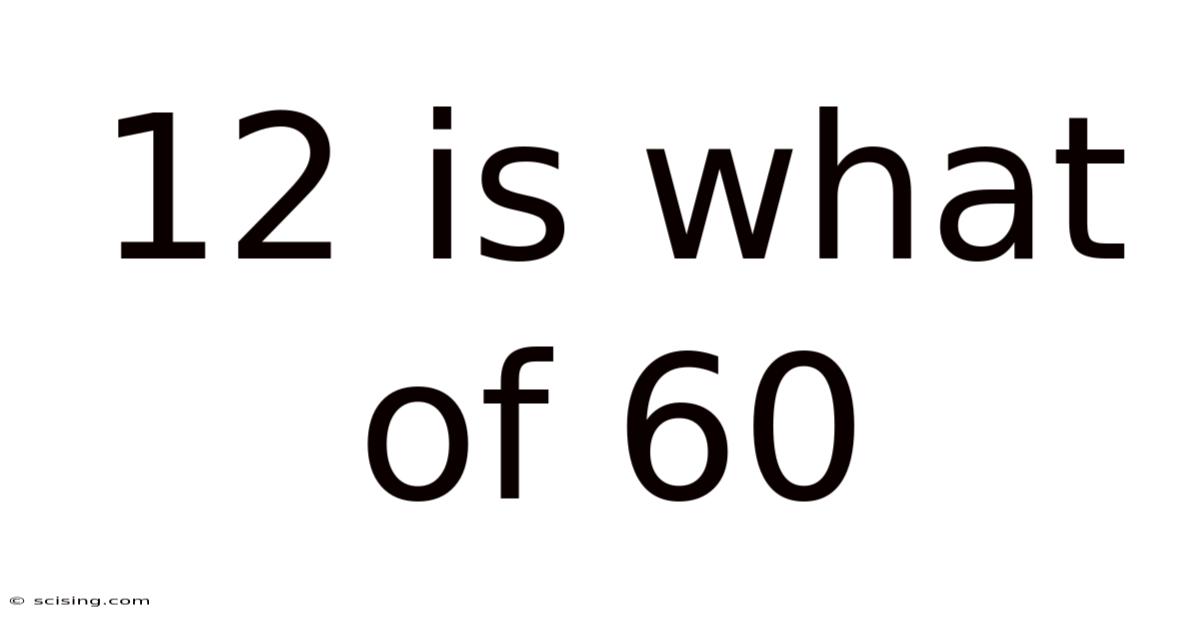
Table of Contents
12 is What Percent of 60? Understanding Percentages and Their Applications
Understanding percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and taxes to analyzing data and understanding financial reports. This article will thoroughly explore the question "12 is what percent of 60?" We'll not only solve this specific problem but also delve into the underlying concepts of percentages, providing you with a comprehensive understanding of how to tackle similar problems and apply this knowledge to various real-world scenarios.
Understanding Percentages: A Foundation
A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2. Percentages are a convenient way to represent proportions and ratios, making comparisons and calculations easier.
Solving "12 is What Percent of 60?"
To determine what percentage 12 represents of 60, we can use the following formula:
(Part / Whole) x 100% = Percentage
In this case:
- Part: 12
- Whole: 60
Substituting these values into the formula:
(12 / 60) x 100% = 0.2 x 100% = 20%
Therefore, 12 is 20% of 60.
Step-by-Step Calculation
Let's break down the calculation into simpler steps for better understanding:
-
Set up the fraction: Express the problem as a fraction: 12/60.
-
Simplify the fraction (optional): Simplifying the fraction makes the calculation easier. 12/60 simplifies to 1/5.
-
Convert the fraction to a decimal: Divide the numerator (12) by the denominator (60). 12 ÷ 60 = 0.2
-
Convert the decimal to a percentage: Multiply the decimal by 100 and add the percentage symbol (%). 0.2 x 100% = 20%
Alternative Method: Using Proportions
Another approach to solve this problem is using proportions. We can set up a proportion where 'x' represents the unknown percentage:
12/60 = x/100
To solve for 'x', we cross-multiply:
60x = 1200
x = 1200 / 60
x = 20
Therefore, x = 20%, confirming our previous result.
Practical Applications of Percentages
Understanding percentages is crucial in numerous real-world situations. Here are a few examples:
-
Calculating discounts: If a store offers a 25% discount on an item priced at $80, you can calculate the discount amount as (25/100) x $80 = $20. The final price would be $80 - $20 = $60.
-
Determining tax amounts: If the sales tax in your area is 6%, and you purchase an item for $50, the tax amount would be (6/100) x $50 = $3. The total cost would be $50 + $3 = $53.
-
Analyzing data: Percentages are widely used to represent data in charts, graphs, and reports. For example, a company might report that 15% of its sales came from a specific product line.
-
Understanding financial statements: Financial statements like income statements and balance sheets utilize percentages extensively to show ratios and trends. For instance, profit margins are often expressed as a percentage of revenue.
-
Calculating interest rates: Interest on loans and investments is typically expressed as a percentage. For example, a 5% interest rate on a $1000 investment means you'll earn $50 in interest in one year (assuming simple interest).
Beyond the Basics: More Complex Percentage Problems
While the problem "12 is what percent of 60?" is relatively straightforward, the principles involved can be applied to more complex scenarios. For instance, you might encounter problems involving:
-
Finding the whole amount: If 30% of a number is 15, what is the number? This involves working backward using the percentage formula.
-
Calculating percentage increase or decrease: Determining the percentage change between two values (e.g., the percentage increase in sales from one year to the next).
-
Compound interest: Calculating interest that is earned not only on the principal amount but also on accumulated interest.
-
Percentage points: Understanding the difference between percentage change and percentage points. A change from 10% to 15% is a 5 percentage point increase, but a 50% increase relative to the original value (10%).
Frequently Asked Questions (FAQ)
Q: What if I don't have a calculator?
A: You can always perform the calculations manually. Remember that dividing by 100 is the same as moving the decimal point two places to the left. For example, 20% is equivalent to 0.20 or 0.2.
Q: Can I use a different method to solve percentage problems?
A: Yes, there are various approaches, including using proportions, setting up equations, and employing mental math techniques for simpler problems. The best method often depends on the specific problem and your comfort level with different mathematical tools.
Q: What are some common mistakes to avoid when working with percentages?
A: Common errors include:
- Confusing percentage change with percentage points.
- Incorrectly applying the percentage formula.
- Rounding errors during calculations.
- Not considering the context of the problem.
Q: Where can I find more practice problems?
A: Many online resources, textbooks, and educational websites offer practice problems on percentages, ranging from basic to more advanced levels.
Conclusion: Mastering Percentages for a Brighter Future
The ability to calculate percentages accurately and efficiently is a valuable life skill. From managing personal finances to understanding complex data, a strong grasp of percentages opens doors to many opportunities. By understanding the basic formula and various methods of calculation, you can confidently tackle diverse problems and apply this knowledge in various aspects of your life. Remember that practice is key – the more you work with percentage problems, the more comfortable and proficient you'll become. Continue practicing, and you'll soon find yourself effortlessly solving even the most challenging percentage calculations. This skill, once mastered, will serve as a valuable asset in your academic and professional endeavors.
Latest Posts
Latest Posts
-
How To Calculate Max Error
Sep 08, 2025
-
Diseases That End In Itis
Sep 08, 2025
-
Law Of Sines Word Problems
Sep 08, 2025
-
Downward Slope Of Demand Curve
Sep 08, 2025
-
Us State Capitals Midwest Region
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about 12 Is What Of 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.