12 Is What Of 30
scising
Sep 07, 2025 · 5 min read
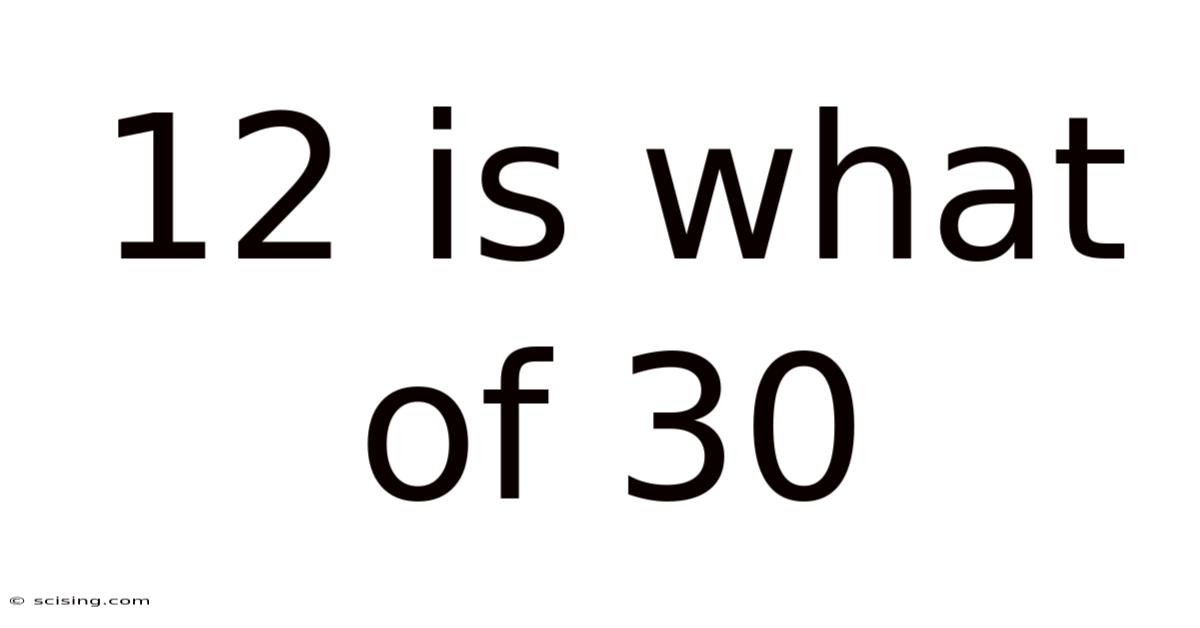
Table of Contents
12 is What Percent of 30? Understanding Percentages and Their Applications
This article explores the fundamental concept of percentages, demonstrating how to calculate what percentage 12 represents of 30. We will delve into the underlying mathematical principles, provide step-by-step instructions, and discuss various real-world applications where understanding percentages is crucial. This guide aims to clarify the concept for anyone, regardless of their mathematical background, making it easy to understand and apply in everyday situations.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred" ("per cent" in Latin). Percentages are used to represent proportions or parts of a whole. For instance, 50% represents 50 out of 100, which is equivalent to one-half (½) or 0.5 as a decimal.
Percentages are ubiquitous in everyday life, from calculating discounts in a store to understanding financial reports, analyzing statistical data, and expressing probabilities. Mastering percentage calculations is essential for navigating numerous aspects of personal and professional life.
Calculating the Percentage: 12 is What Percent of 30?
To determine what percentage 12 represents of 30, we need to follow a straightforward process:
Step 1: Set up the equation
First, express the relationship as a fraction: 12/30. This fraction represents the part (12) relative to the whole (30).
Step 2: Convert the fraction to a decimal
Divide the numerator (12) by the denominator (30): 12 ÷ 30 = 0.4
Step 3: Convert the decimal to a percentage
Multiply the decimal by 100%: 0.4 × 100% = 40%
Therefore, 12 is 40% of 30.
Different Approaches to Calculating Percentages
While the method above is the most straightforward, other approaches can be equally effective. Let's explore a couple of alternative methods:
Method 2: Using Proportions
We can set up a proportion to solve this problem. A proportion is an equation stating that two ratios are equal. We can represent this as:
12/30 = x/100
Where 'x' represents the percentage we are trying to find. To solve for 'x', we can cross-multiply:
30x = 1200
x = 1200 / 30
x = 40
Therefore, x = 40%, confirming our previous result.
Method 3: Using the Percentage Formula
The percentage formula provides a more direct approach:
Percentage = (Part / Whole) x 100%
In this case:
Percentage = (12 / 30) x 100% = 40%
Real-World Applications of Percentage Calculations
Understanding percentages is a critical life skill applicable in many contexts:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely heavily on percentage calculations. For instance, a 10% discount on a $100 item would save you $10. Understanding compound interest, which involves applying percentages repeatedly, is crucial for long-term financial planning.
-
Retail and Sales: Retailers frequently use percentages to advertise sales and discounts, attracting customers with attractive offers. Salespeople often earn commissions based on a percentage of their sales. Analyzing sales figures and trends also involves working with percentages.
-
Statistics and Data Analysis: Percentages are fundamental to representing data in a clear and concise manner. Statistical reports, surveys, and opinion polls commonly use percentages to summarize and present findings. For example, understanding the percentage of respondents who favor a particular candidate in an election poll is crucial for interpreting the results.
-
Science and Research: Percentages play a significant role in scientific research, especially in expressing experimental results, analyzing data sets, and expressing probabilities. For example, calculating the percentage of successful trials in an experiment helps researchers understand the effectiveness of their procedures.
-
Everyday Life: Calculating tips in restaurants, determining the percentage of ingredients in a recipe, understanding nutritional information on food labels, and even calculating your grade in a class all involve percentages.
Common Percentage Calculations: Beyond the Basics
While calculating "12 is what percent of 30" is a straightforward example, let's consider some related scenarios:
-
Finding a Percentage of a Number: To find 40% of 75, we multiply 75 by 0.4 (40% expressed as a decimal): 75 * 0.4 = 30.
-
Finding the Whole when Given a Part and Percentage: If 25% of a number is 15, we can set up an equation: 0.25x = 15. Solving for x (the whole number), we get x = 15 / 0.25 = 60.
-
Finding the Percentage Increase or Decrease: If a quantity increases from 50 to 60, the percentage increase is calculated as: [(60-50)/50] x 100% = 20%. Similarly, if it decreases from 60 to 50, the percentage decrease is 16.67%.
Avoiding Common Mistakes in Percentage Calculations
Several common errors can occur when working with percentages:
-
Confusing Part and Whole: Carefully identify which number represents the part and which represents the whole.
-
Incorrect Decimal Conversions: Ensure you convert percentages to decimals correctly before performing calculations (e.g., 25% = 0.25).
-
Rounding Errors: Be mindful of rounding errors, especially when dealing with multiple calculations involving percentages.
Frequently Asked Questions (FAQ)
-
Q: Why are percentages useful?
-
A: Percentages provide a standardized way to compare proportions, making it easy to understand relative amounts and facilitate decision-making in various contexts.
-
Q: Can percentages be greater than 100%?
-
A: Yes, percentages can exceed 100%, indicating that a quantity has increased beyond its initial value. For example, a 150% increase means the quantity has grown to 1.5 times its original value.
-
Q: How do I calculate a percentage change?
-
A: Percentage change = [(New Value - Old Value) / Old Value] x 100%. A positive result indicates an increase, while a negative result indicates a decrease.
Conclusion: Mastering Percentages for a Brighter Future
Understanding percentages is a fundamental skill applicable across various aspects of life. From managing personal finances to analyzing data and interpreting research, the ability to calculate and interpret percentages empowers informed decision-making. This article has provided a comprehensive guide to understanding and calculating percentages, equipping readers with the knowledge and confidence to tackle percentage-related problems effectively. Remember the basic principles, practice different approaches, and be cautious of common mistakes. By mastering these concepts, you'll enhance your numerical literacy and improve your ability to navigate the quantitative demands of everyday life and professional endeavors. The ability to confidently handle percentage calculations opens doors to greater understanding and success in many fields.
Latest Posts
Latest Posts
-
Dna Pol Vs Rna Pol
Sep 08, 2025
-
Euclidean And Non Euclidean Geometry
Sep 08, 2025
-
5 Us Gallon To Kg
Sep 08, 2025
-
Upside Down T In Geometry
Sep 08, 2025
-
Vassals In The Middle Ages
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about 12 Is What Of 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.