11 Out Of 25 Percentage
scising
Sep 21, 2025 · 5 min read
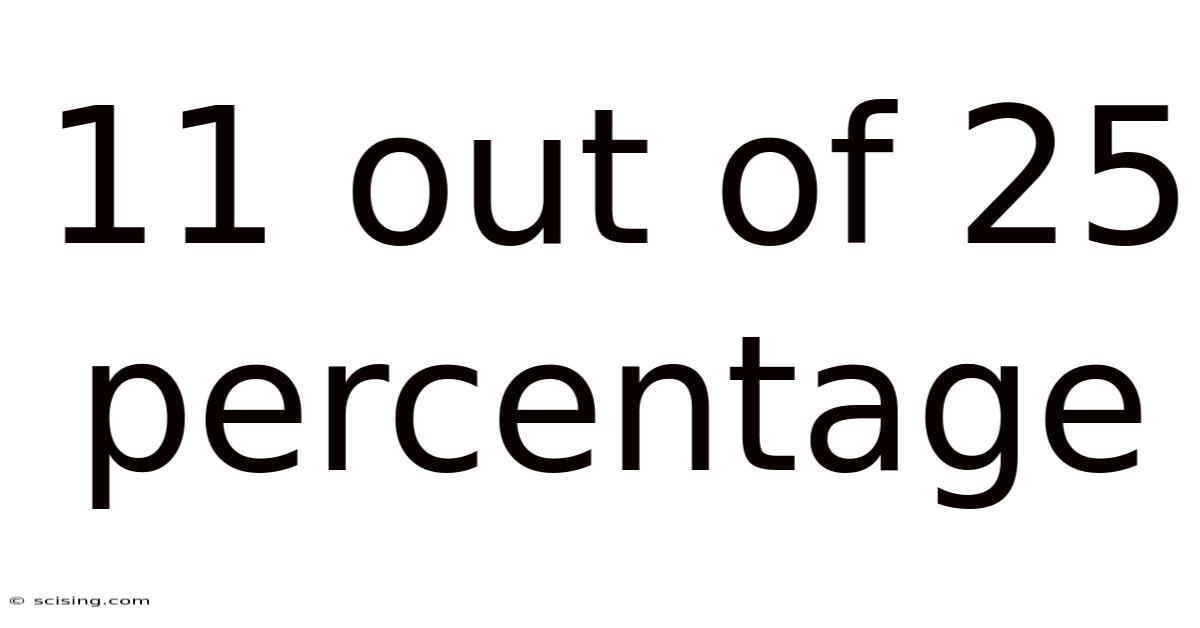
Table of Contents
Understanding 11 out of 25: A Comprehensive Guide to Percentages and Proportions
Understanding percentages is a fundamental skill in mathematics with applications spanning various fields, from everyday finances to advanced scientific calculations. This article delves into the meaning and calculation of "11 out of 25," explaining not only the numerical answer but also the underlying concepts and practical applications. We'll explore different methods of calculation, address common misconceptions, and provide a solid foundation for understanding proportions and percentages.
Introduction: Deciphering the Fraction
The phrase "11 out of 25" represents a fraction. Fractions express a part of a whole. In this case, 11 is the part, and 25 is the whole. To understand the percentage, we need to convert this fraction into a percentage, which represents the proportion as a fraction of 100. This is crucial for comparing different proportions and making informed decisions in various contexts.
Method 1: Direct Conversion to Percentage
The most straightforward method involves converting the fraction into a decimal and then multiplying by 100.
-
Convert the fraction to a decimal: Divide the part (11) by the whole (25): 11 ÷ 25 = 0.44
-
Multiply the decimal by 100: 0.44 x 100 = 44%
Therefore, 11 out of 25 is equal to 44%.
Method 2: Using Proportions
This method utilizes the concept of proportions, demonstrating the relationship between the fraction and its percentage equivalent. We set up a proportion:
- 11/25 = x/100
Where 'x' represents the percentage we want to find. To solve for 'x', we cross-multiply:
- 11 * 100 = 25 * x
- 1100 = 25x
- x = 1100 / 25
- x = 44
Again, we find that 11 out of 25 is 44%.
Method 3: Simplifying the Fraction (Optional)
While not strictly necessary for this particular problem, simplifying fractions can make calculations easier, especially with larger numbers. In this case, 11 and 25 don't share any common factors other than 1, meaning the fraction is already in its simplest form. However, let's illustrate with an example where simplification is beneficial. If we had 20 out of 50, we could simplify the fraction to 2/5 before converting to a percentage:
-
Simplify: 20/50 simplifies to 2/5
-
Convert to decimal: 2 ÷ 5 = 0.4
-
Multiply by 100: 0.4 x 100 = 40%
Practical Applications of Percentages:
Understanding percentages has broad applicability in everyday life and various professions:
-
Finance: Calculating interest rates, discounts, tax rates, and profit margins all rely on percentage calculations. For instance, understanding that a 44% discount on a product means you save 44% of the original price is crucial for making informed purchasing decisions.
-
Statistics: Percentages are essential for interpreting statistical data, representing proportions within a population, and analyzing trends. For example, if a survey shows 44% of respondents prefer a particular product, this percentage provides valuable insight into consumer preference.
-
Science: Percentages are used extensively in scientific research to express concentrations, error rates, and experimental yields. For example, a 44% yield in a chemical reaction indicates the efficiency of the process.
-
Education: Grading systems often utilize percentages to represent a student's performance relative to the total possible score. Achieving 44% on an exam indicates the portion of questions answered correctly.
Common Misconceptions about Percentages:
-
Confusing Percentages with Absolute Values: A 44% increase in something does not mean it has increased by 44 units. It means it has increased by 44% of its original value.
-
Incorrect Addition/Subtraction of Percentages: You cannot simply add or subtract percentages directly without considering the base values involved. For instance, a 10% increase followed by a 10% decrease does not result in the original value.
-
Misinterpreting Percentage Changes: A percentage change describes the relative change compared to the original value. Understanding the context is crucial; a 10% increase on a small number will be less significant than a 10% increase on a large number.
Beyond the Basics: Understanding Proportions in Depth
The calculation of 11 out of 25 demonstrates a fundamental principle in mathematics: proportions. Proportions describe the relationship between two or more quantities. Understanding proportions helps in solving various problems involving ratios, scales, and comparisons.
For example, consider a recipe that calls for 11 cups of flour for every 25 cups of water. If you want to make a smaller batch using only 5 cups of water, you would need to maintain the proportion:
- 11/25 = x/5
Cross-multiplying and solving for 'x', you'll find you need 2.2 cups of flour.
Further Applications and Extensions:
The concept extends beyond simple calculations. Consider these examples:
-
Probability: If you have a bag containing 25 marbles, 11 of which are red, the probability of drawing a red marble is 11/25 or 44%.
-
Data Analysis: In data sets, percentages help to visualize and interpret trends. For example, the percentage of customers who make repeat purchases can indicate customer loyalty.
Frequently Asked Questions (FAQ):
-
Q: How do I calculate a percentage increase or decrease?
- A: To calculate a percentage increase, find the difference between the new value and the original value, divide by the original value, and multiply by 100. For a percentage decrease, follow the same process but interpret the result as a negative percentage.
-
Q: What if I have a more complex fraction, like 17 out of 68?
- A: Follow the same methods. First, simplify the fraction if possible (17/68 simplifies to 1/4), then convert to a decimal and multiply by 100. In this case, 1/4 is 0.25, and 0.25 x 100 = 25%.
-
Q: Are there any online calculators for percentages?
- A: Yes, many online calculators are available that can perform percentage calculations quickly and easily.
-
Q: How can I improve my understanding of percentages?
- A: Practice is key! Work through various examples, including those involving percentage increases, decreases, and applications in different contexts.
Conclusion: Mastering the Art of Percentages
Understanding "11 out of 25" as 44% is more than just a numerical calculation. It's about grasping the fundamental concept of proportions and their significance in various fields. By mastering percentage calculations and applying the principles of proportions, you equip yourself with a powerful tool for navigating the numerical world and making informed decisions in your daily life and professional endeavors. Remember that the key to success lies in consistent practice and a thorough understanding of the underlying concepts. With dedication and practice, you can confidently tackle any percentage-related problem.
Latest Posts
Latest Posts
-
Church On Fire The Outsiders
Sep 21, 2025
-
Cda Practice Test 65 Questions
Sep 21, 2025
-
Squealer From Animal Farm Quotes
Sep 21, 2025
-
The Chorus Of A Song
Sep 21, 2025
-
Can We Meet In Spanish
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 11 Out Of 25 Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.