11 25 As A Percent
scising
Sep 21, 2025 · 6 min read
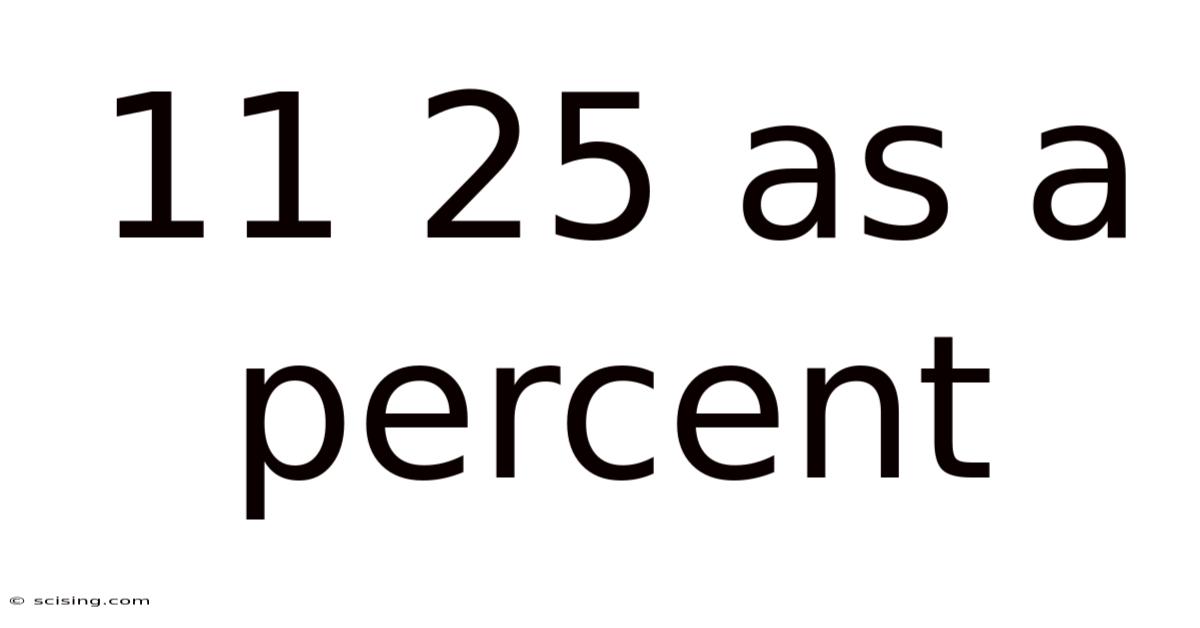
Table of Contents
11/25 as a Percent: A Comprehensive Guide to Fraction-to-Percentage Conversion
Understanding how to convert fractions to percentages is a fundamental skill in mathematics with widespread applications in everyday life, from calculating discounts to understanding statistical data. This comprehensive guide will walk you through the process of converting the fraction 11/25 into a percentage, exploring various methods and providing a deeper understanding of the underlying concepts. We'll also delve into the practical implications and address frequently asked questions.
Understanding Fractions and Percentages
Before we dive into the conversion, let's briefly revisit the definitions of fractions and percentages.
A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts we have, and the denominator indicates the total number of parts the whole is divided into. In our case, 11/25 means we have 11 parts out of a total of 25 parts.
A percentage, denoted by the symbol %, represents a fraction out of 100. It expresses a proportion relative to a whole, where the whole is considered as 100%. For example, 50% means 50 parts out of 100, or 50/100, which simplifies to 1/2.
Method 1: Converting the Fraction to a Decimal, then to a Percentage
This is arguably the most straightforward method. We first convert the fraction 11/25 into a decimal and then multiply the decimal by 100 to obtain the percentage.
-
Divide the numerator by the denominator: 11 ÷ 25 = 0.44
-
Multiply the decimal by 100: 0.44 × 100 = 44
-
Add the percentage symbol: 44%
Therefore, 11/25 is equal to 44%.
This method is easily adaptable to any fraction. Simply divide the numerator by the denominator and multiply the result by 100.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
This method leverages the definition of percentage as a fraction out of 100. We aim to find an equivalent fraction to 11/25 that has a denominator of 100.
To do this, we ask: "What number do we multiply 25 by to get 100?" The answer is 4 (25 x 4 = 100).
Since we multiply the denominator by 4, we must also multiply the numerator by 4 to maintain the equivalence of the fraction.
-
Multiply both the numerator and denominator by 4: (11 x 4) / (25 x 4) = 44/100
-
Express as a percentage: 44/100 = 44%
This method emphasizes the conceptual understanding of percentages as parts of 100. It's particularly helpful for fractions where the denominator is a factor of 100 (such as 25, 50, and others).
Method 3: Using Proportions
This method uses the concept of proportions to solve for the percentage. We set up a proportion where the fraction 11/25 is equal to x/100, where x represents the percentage.
-
Set up the proportion: 11/25 = x/100
-
Cross-multiply: 11 * 100 = 25 * x
-
Solve for x: 1100 = 25x => x = 1100/25 = 44
-
Express as a percentage: x = 44%
This method highlights the relationship between fractions and percentages as equivalent ratios. It's a powerful technique applicable to more complex scenarios.
Practical Applications of Percentage Conversions
The ability to convert fractions to percentages is crucial in numerous real-world situations:
-
Calculating discounts: If a store offers a 20% discount on an item, you can use this knowledge to determine the actual price reduction.
-
Understanding financial statements: Financial reports often use percentages to represent key performance indicators (KPIs) like profit margins and growth rates.
-
Interpreting statistical data: Percentages are frequently employed to present survey results, election outcomes, and other statistical analyses.
-
Calculating grades: Your final grade in a course might be calculated based on your performance on various assignments, with each assignment contributing a specific percentage to the final score.
-
Determining tax rates: Tax rates are often expressed as percentages to calculate the amount of tax owed on income or purchases.
-
Cooking and baking: Recipes often use fractions, but converting them to percentages can be helpful for scaling up or down recipes.
These are just a few examples, highlighting the ubiquitous use of percentage calculations in our daily lives. Mastery of fraction-to-percentage conversions equips you to tackle these challenges efficiently and accurately.
Why is Understanding Percentage Conversions Important?
Beyond the immediate practical applications, the ability to convert fractions to percentages fosters a deeper understanding of mathematical concepts:
-
Proportional reasoning: Understanding percentages enhances your ability to analyze and interpret proportional relationships.
-
Number sense: Fluency in percentage conversions strengthens your overall number sense and mathematical intuition.
-
Problem-solving skills: This skill forms a building block for tackling more complex mathematical problems and real-world challenges.
-
Data analysis: Interpreting data expressed in percentages is a valuable skill in various fields, including science, business, and social studies.
Developing a strong foundation in percentage conversion is an investment in your mathematical literacy and problem-solving capabilities.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to convert fractions to percentages?
A: Yes, absolutely! Most calculators have a function to perform this conversion directly. Simply divide the numerator by the denominator and then multiply by 100.
Q: What if the fraction results in a repeating decimal?
A: If the division results in a repeating decimal, you can round the decimal to a certain number of decimal places to express the percentage. For instance, 1/3 = 0.333... You can round this to 0.33 and express it as 33%.
Q: Are there any online tools to help with fraction-to-percentage conversion?
A: Yes, many online calculators and converters are available. You can easily find them by searching "fraction to percentage converter" on a search engine.
Q: How can I improve my understanding of fractions and percentages?
A: Practice is key! Work through various examples, starting with simple fractions and gradually increasing the complexity. You can also find helpful resources online and in textbooks.
Conclusion
Converting 11/25 to a percentage, which equals 44%, is a simple yet fundamental mathematical skill. Understanding the various methods—converting to a decimal, finding an equivalent fraction with a denominator of 100, and using proportions—enhances your mathematical comprehension and provides valuable tools for real-world applications. Mastering this skill not only improves your problem-solving ability but also strengthens your numerical reasoning and data analysis skills, proving invaluable in various aspects of life and numerous academic and professional fields. Regular practice and exploration of different methods will further solidify your understanding and proficiency in this important area of mathematics.
Latest Posts
Latest Posts
-
Texas Regions Mountains And Basins
Sep 21, 2025
-
Is Mgbr2 Ionic Or Covalent
Sep 21, 2025
-
Moment Of Inertia For Rod
Sep 21, 2025
-
Half Human And Half Goat
Sep 21, 2025
-
What Does Sensory Details Mean
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 11 25 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.