10/3 As A Mixed Number
scising
Sep 19, 2025 · 6 min read
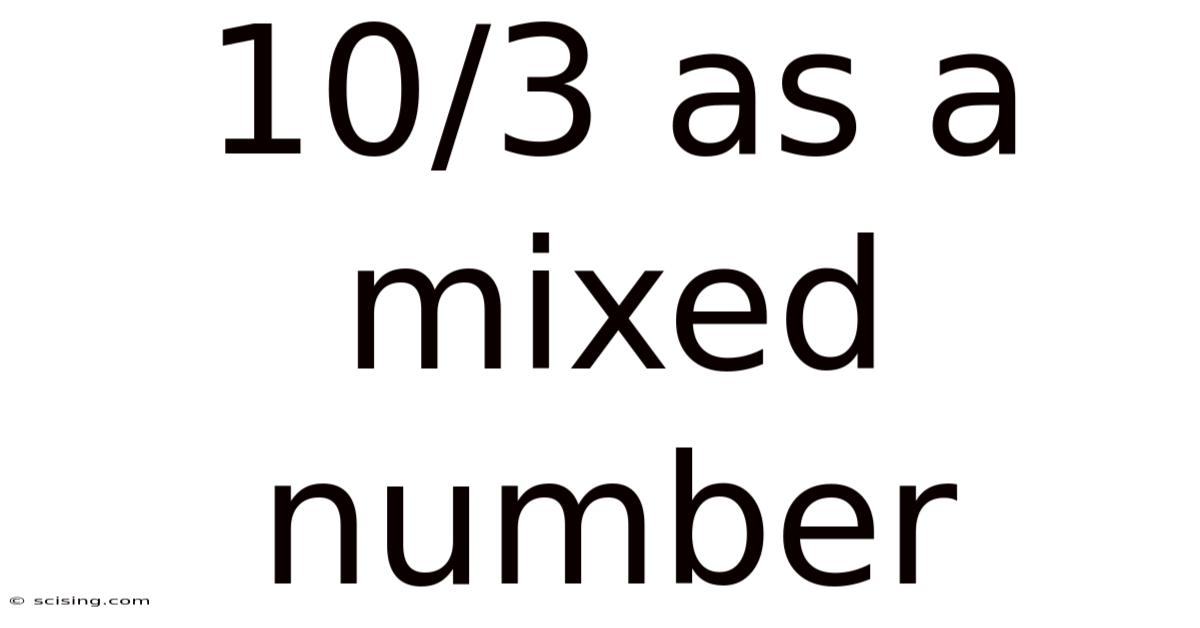
Table of Contents
Understanding 10/3 as a Mixed Number: A Comprehensive Guide
The fraction 10/3, also known as ten-thirds, represents ten equal parts of a whole divided into three parts. While perfectly valid in its current form, understanding how to express this improper fraction as a mixed number is crucial in various mathematical contexts. This comprehensive guide will delve into the process of converting 10/3 into a mixed number, explore the underlying concepts, and provide practical examples to solidify your understanding. We'll also address frequently asked questions and provide additional insights to enhance your fractional literacy.
What is a Mixed Number?
A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (top number) is smaller than the denominator (bottom number). For example, 1 ¾, 2 ⅓, and 5 ⅛ are all mixed numbers. They represent a quantity greater than one whole unit.
Converting 10/3 to a Mixed Number: A Step-by-Step Approach
Converting an improper fraction (like 10/3, where the numerator is larger than the denominator) to a mixed number involves dividing the numerator by the denominator. Here's the process:
-
Division: Divide the numerator (10) by the denominator (3). 10 ÷ 3 = 3 with a remainder of 1.
-
Whole Number: The quotient (the result of the division) becomes the whole number part of the mixed number. In this case, the quotient is 3.
-
Fraction: The remainder (1) becomes the numerator of the fraction, and the denominator remains the same (3). This gives us the fraction 1/3.
-
Combining: Combine the whole number and the fraction to form the mixed number. Therefore, 10/3 as a mixed number is 3 ⅓.
Visualizing the Conversion
Imagine you have 10 slices of pizza, and each pizza is cut into 3 slices. You can assemble 3 complete pizzas (3 x 3 = 9 slices) with one slice remaining. This visually represents the mixed number 3 ⅓. Each whole pizza represents the whole number 3, and the remaining slice represents the fraction 1/3.
The Importance of Understanding Mixed Numbers
Mixed numbers are essential for several reasons:
-
Real-world applications: Many real-world measurements and quantities are expressed using mixed numbers. For instance, you might measure a piece of wood as 2 ⅝ feet or bake a cake using 1 ½ cups of sugar.
-
Simplifying calculations: Mixed numbers can sometimes simplify calculations, particularly when dealing with addition and subtraction of fractions. It's often easier to add 2 ½ + 1 ¼ than to add 5/2 + 5/4.
-
Improved comprehension: Mixed numbers offer a more intuitive representation of quantities greater than one. They provide a clearer picture of the magnitude of the value compared to an improper fraction.
Working with Mixed Numbers: Addition and Subtraction
Adding and subtracting mixed numbers requires a slightly different approach than adding and subtracting proper fractions. Here’s a breakdown of the process:
Addition:
-
Convert to Improper Fractions (Optional): While not strictly necessary, converting both mixed numbers to improper fractions can simplify the addition process. For example, to add 3 ⅓ + 2 ½, convert them to 10/3 + 5/2. Find a common denominator (6) and add: (20/6) + (15/6) = 35/6.
-
Add the Whole Numbers and Fractions Separately (Alternative): Alternatively, add the whole numbers separately and the fractions separately. Then simplify. For example 3 ⅓ + 2 ½ = (3 + 2) + (⅓ + ½) = 5 + (2/6 + 3/6) = 5 + 5/6 = 5 ⅚
-
Convert back to a Mixed Number (if necessary): If the result is an improper fraction, convert it back to a mixed number. In the first example, 35/6 simplifies to 5 ⅚.
Subtraction:
The process for subtraction is similar.
-
Convert to Improper Fractions (Optional): Converting to improper fractions is often helpful to avoid complications.
-
Subtract the Whole Numbers and Fractions Separately (Alternative): Similar to addition, it’s possible to perform subtraction on the whole numbers and fractions separately. However, ensure borrowing from the whole number if the fractional part of the first number is less than the fractional part of the second number. For example, 3 ½ - 1 ⅔ necessitates borrowing. Rewrite 3 ½ as 2 5/2. Then 2 5/2 - 1 ⅔ = 1 (5/2 - 4/3) = 1 (15/6 - 8/6) = 1 ⁷⁄₆ = 2 ⅛.
-
Convert back to a Mixed Number (if necessary): Convert the result back to a mixed number if it's an improper fraction.
Beyond 10/3: Generalizing the Conversion Process
The process of converting an improper fraction to a mixed number remains the same regardless of the numerator and denominator. Always divide the numerator by the denominator. The quotient becomes the whole number, and the remainder becomes the numerator of the new fraction, keeping the original denominator.
For example:
- 17/5: 17 ÷ 5 = 3 with a remainder of 2, resulting in the mixed number 3 ⅖.
- 23/7: 23 ÷ 7 = 3 with a remainder of 2, resulting in the mixed number 3 ⅖.
- 41/9: 41 ÷ 9 = 4 with a remainder of 5, resulting in the mixed number 4 ⅑.
Frequently Asked Questions (FAQ)
Q: Why is it important to learn how to convert improper fractions to mixed numbers?
A: Mixed numbers provide a more intuitive and user-friendly representation of quantities larger than one. They are crucial for real-world applications and often simplify calculations in various mathematical contexts.
Q: Can I always convert an improper fraction into a mixed number?
A: Yes, any improper fraction can be converted into a mixed number.
Q: What if the remainder is zero after dividing the numerator by the denominator?
A: If the remainder is zero, it means the improper fraction is actually a whole number. For example, 12/3 = 4. There's no fractional part in the mixed number.
Q: Is there only one way to represent a quantity?
A: No, a single quantity can be represented in multiple ways. For example, 10/3, 3 ⅓, and 3.333... (a recurring decimal) all represent the same quantity. The choice of representation depends on the context and the desired level of precision.
Conclusion
Understanding how to convert an improper fraction like 10/3 into a mixed number (3 ⅓) is a fundamental skill in mathematics. This process, involving division and the interpretation of the quotient and remainder, allows for a more intuitive representation of quantities greater than one. Mastering this conversion, along with understanding the addition and subtraction of mixed numbers, equips you with essential tools for tackling various mathematical problems and real-world applications. Remember that practice is key to solidifying your understanding and building confidence in working with fractions. The more you practice, the more comfortable and proficient you will become.
Latest Posts
Latest Posts
-
Treble Clef Lines And Spaces
Sep 20, 2025
-
Princess And The Pea Film
Sep 20, 2025
-
Money Weighted Rate Of Return
Sep 20, 2025
-
Map Of The Middle Colonies
Sep 20, 2025
-
Is The U S An Empire
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 10/3 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.