1 Million Divided By 20
scising
Sep 15, 2025 · 6 min read
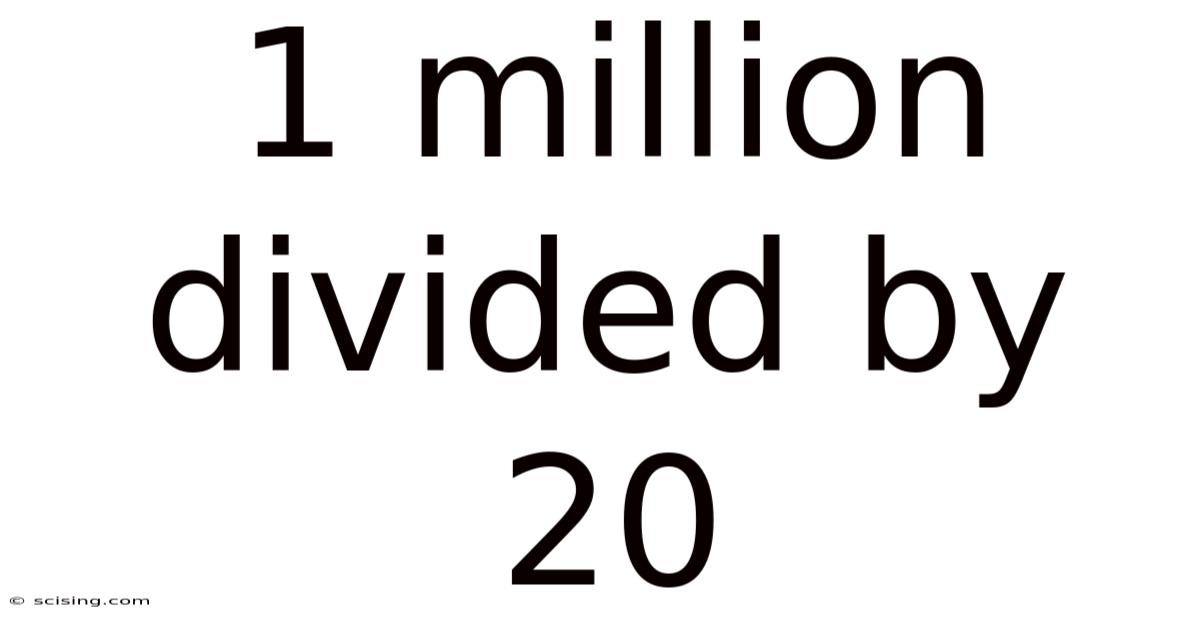
Table of Contents
One Million Divided by Twenty: A Deep Dive into Division and its Applications
This article explores the seemingly simple calculation of one million divided by twenty (1,000,000 ÷ 20), delving beyond the immediate answer to uncover the underlying mathematical principles, practical applications, and related concepts. Understanding this division problem provides a foundation for grasping larger mathematical concepts and problem-solving strategies. We will cover the calculation itself, explore different methods to arrive at the answer, and discuss real-world scenarios where this type of calculation is crucial.
I. The Straightforward Calculation: 1,000,000 ÷ 20
The most direct approach is to perform long division. However, we can simplify this significantly by recognizing that 20 is a multiple of 10. We can rewrite the problem as:
1,000,000 ÷ (2 x 10)
This allows us to break the problem down into smaller, more manageable steps. First, divide 1,000,000 by 10. This is easily done by simply removing one zero from the end of the number, resulting in 100,000. Now, we divide this result by 2:
100,000 ÷ 2 = 50,000
Therefore, 1,000,000 ÷ 20 = 50,000.
II. Alternative Methods and Conceptual Understanding
While the above method is efficient, exploring alternative approaches enhances our understanding of the core concepts.
-
Using Fractions: We can represent the division as a fraction: 1,000,000/20. Simplifying this fraction involves finding common factors between the numerator and the denominator. Both numbers are divisible by 10, and further by 2:
(1,000,000 ÷ 10) / (20 ÷ 10) = 100,000 / 2 = 50,000
-
Repeated Subtraction: While not the most practical method for large numbers, understanding repeated subtraction illustrates the fundamental concept of division. Imagine subtracting 20 repeatedly from 1,000,000 until you reach zero. The number of times you subtract 20 represents the quotient (the answer). This method is helpful for visualizing the process, especially for beginners.
-
Using a Calculator: Modern calculators provide a quick and easy way to solve this problem. Simply enter 1,000,000 ÷ 20 and press the equals button to get the answer, 50,000. While convenient, understanding the underlying mathematical principles is crucial for problem-solving beyond simple calculations.
III. Real-World Applications: Where This Calculation Matters
The division of one million by twenty, though seemingly abstract, has practical relevance across various fields:
-
Finance and Budgeting: Imagine a company with annual revenue of $1,000,000 that allocates 20% of its revenue to marketing. Dividing 1,000,000 by 20 (or multiplying by 0.05 which is the same as dividing by 20) gives us $50,000, the marketing budget. This type of calculation is fundamental in financial planning and resource allocation.
-
Population Distribution: Consider a city with a population of 1,000,000 people divided into 20 districts. Dividing the total population by the number of districts gives the average population per district (50,000). This is useful in understanding population density and resource distribution within the city.
-
Inventory Management: A warehouse with 1,000,000 units of a product needs to distribute them evenly across 20 different stores. Each store would receive 50,000 units. This type of calculation is vital for inventory management and supply chain optimization.
-
Data Analysis and Statistics: In statistical analysis, calculating averages or means often involves division. If you have 1,000,000 data points grouped into 20 categories, finding the average number of data points per category would require this calculation.
-
Engineering and Construction: In large-scale projects, calculating material requirements, workforce allocation, or project timelines often involves dividing large numbers into smaller, more manageable units.
IV. Expanding the Concept: Working with Larger and Smaller Numbers
The principle behind dividing 1,000,000 by 20 applies to a wide range of division problems. By understanding the underlying logic, we can tackle more complex scenarios.
Consider the following examples:
-
10,000,000 ÷ 20: Using the same principles, we can quickly determine the answer to be 500,000. Notice the pattern: adding a zero to the dividend (the number being divided) adds a zero to the quotient (the answer).
-
1,000,000 ÷ 40: Since 40 = 20 x 2, we can first divide 1,000,000 by 20 (resulting in 50,000), and then divide this result by 2, giving us 25,000.
-
1,000,000 ÷ 5: This involves dividing by a smaller number. We can still utilize the same principles, or simply recognize that 20 is four times 5, meaning the answer will be four times larger than when dividing by 20. This results in 200,000.
V. Understanding Remainders and Decimal Results
While 1,000,000 divides evenly by 20, not all divisions result in whole numbers. Sometimes, a remainder exists. For instance, if we divide 1,000,001 by 20, we get 50,000 with a remainder of 1. This remainder can be expressed as a fraction (1/20) or a decimal (0.05). Understanding remainders and decimal results is crucial for many real-world applications.
VI. Connecting Division to Other Mathematical Operations
Division is closely related to other fundamental arithmetic operations:
-
Multiplication: Division is the inverse operation of multiplication. 50,000 x 20 = 1,000,000. This relationship is vital in checking the accuracy of division calculations.
-
Addition and Subtraction: Division can be visualized through repeated subtraction, as discussed earlier. Similarly, multiplication can be seen as repeated addition. These connections highlight the interconnectedness of basic arithmetic operations.
VII. Frequently Asked Questions (FAQ)
-
Q: What is the easiest way to divide 1,000,000 by 20?
- A: The easiest way is to divide by 10 first (resulting in 100,000) and then divide by 2 (resulting in 50,000).
-
Q: What if the numbers are much larger?
- A: The same principles apply. Break down the problem into smaller, manageable steps or use a calculator for efficiency.
-
Q: What is the importance of understanding the underlying mathematical principles?
- A: Understanding the underlying principles allows you to solve more complex problems, adapt to different situations, and check your work for accuracy. It's more than just getting the right answer; it’s about understanding why it’s the right answer.
-
Q: How can I improve my division skills?
- A: Practice regularly with different numbers and problem types. Start with simpler problems and gradually increase the difficulty. Try different methods to reinforce your understanding.
VIII. Conclusion:
The seemingly simple calculation of 1,000,000 ÷ 20 serves as a gateway to a deeper understanding of division and its numerous applications. Beyond the answer of 50,000, lies a world of mathematical concepts and practical uses that permeate various aspects of our lives. By mastering this fundamental operation and understanding its underlying principles, we build a strong foundation for tackling more complex mathematical challenges and problem-solving scenarios in diverse fields. The ability to confidently and efficiently perform this type of calculation empowers us to analyze data, manage resources, and make informed decisions across many areas.
Latest Posts
Latest Posts
-
What Are Aliquots In Chemistry
Sep 15, 2025
-
What Times What Makes 48
Sep 15, 2025
-
Fahrenheit 451 Quotes About Censorship
Sep 15, 2025
-
Symbols Of Childhood In Persepolis
Sep 15, 2025
-
What Are Sandra Cisneros Interests Passions
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 1 Million Divided By 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.