1 Divided By 1 3
scising
Sep 02, 2025 · 5 min read
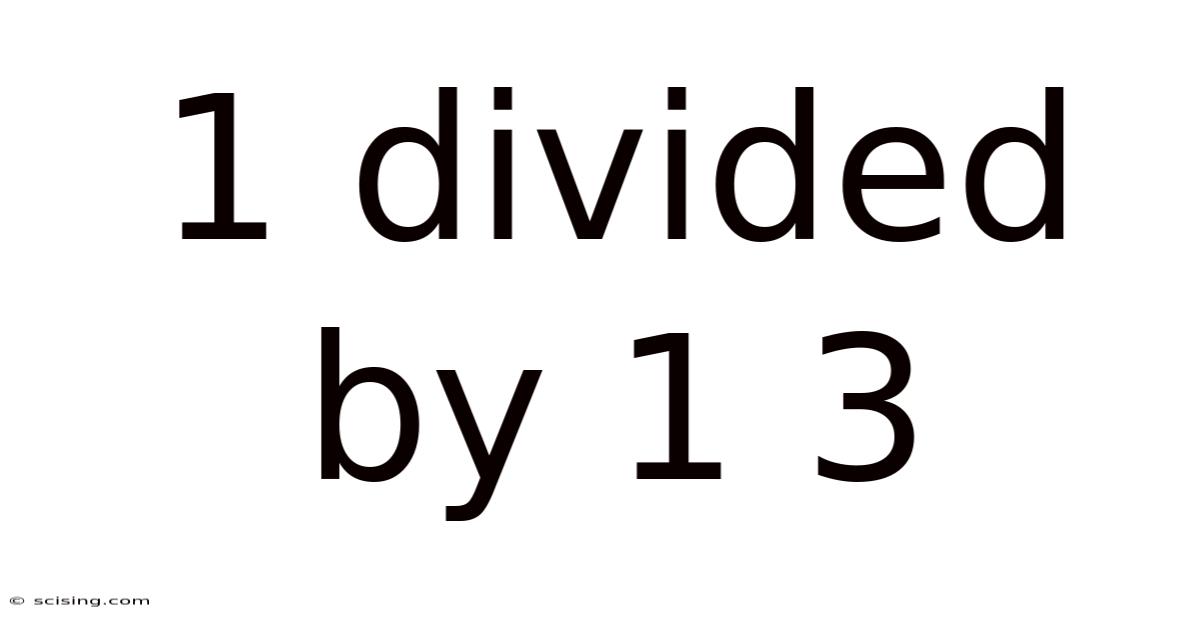
Table of Contents
Unveiling the Mystery: 1 Divided by 1 ⅓ (and Mastering Fraction Division)
This article delves into the seemingly simple yet surprisingly nuanced topic of dividing 1 by 1 ⅓. We'll explore the process step-by-step, explaining the underlying mathematical principles and providing a deeper understanding of fraction division. This comprehensive guide is perfect for anyone wanting to solidify their understanding of fractions, from students brushing up on their math skills to adults looking to refresh their knowledge. Understanding this concept lays the groundwork for tackling more complex mathematical problems.
Understanding Fractions: A Quick Refresher
Before diving into the division problem, let's quickly review the basics of fractions. A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts you have, while the denominator indicates how many parts make up the whole. For example, in the fraction ¾, the numerator is 3 (you have 3 parts) and the denominator is 4 (the whole is divided into 4 parts).
Mixed numbers, like 1 ⅓, combine a whole number and a fraction. In this case, we have one whole and one-third of another. To perform calculations, it's often easier to convert mixed numbers into improper fractions. An improper fraction has a numerator larger than or equal to its denominator.
Converting Mixed Numbers to Improper Fractions
Converting 1 ⅓ into an improper fraction involves these steps:
- Multiply the whole number by the denominator: 1 x 3 = 3
- Add the numerator to the result: 3 + 1 = 4
- Keep the same denominator: The denominator remains 3.
Therefore, 1 ⅓ is equivalent to the improper fraction ⁴⁄₃.
Dividing Fractions: The Reciprocal Method
Dividing fractions involves a crucial concept: the reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of ¾ is ¾.
To divide one fraction by another, we follow these steps:
- Convert any mixed numbers to improper fractions: As we've already done with 1 ⅓.
- Change the division sign to a multiplication sign: This is the key step.
- Replace the second fraction (the divisor) with its reciprocal: Flip the second fraction.
- Multiply the numerators together: Multiply the top numbers.
- Multiply the denominators together: Multiply the bottom numbers.
- Simplify the resulting fraction (if possible): Reduce the fraction to its lowest terms.
Solving 1 ÷ 1 ⅓ Step-by-Step
Now, let's apply these steps to solve 1 ÷ 1 ⅓:
- Convert 1 ⅓ to an improper fraction: As calculated above, 1 ⅓ = ⁴⁄₃.
- Rewrite the problem: The problem becomes 1 ÷ ⁴⁄₃.
- Convert the whole number to a fraction: The whole number 1 can be written as ¹⁄₁.
- Change the division to multiplication and use the reciprocal: ¹⁄₁ ÷ ⁴⁄₃ becomes ¹⁄₁ x ³⁄₄.
- Multiply the numerators: 1 x 3 = 3
- Multiply the denominators: 1 x 4 = 4
- Simplify the resulting fraction: The resulting fraction is ³⁄₄. This fraction is already in its simplest form.
Therefore, 1 ÷ 1 ⅓ = ¾.
Visualizing the Solution
Imagine you have one whole pizza. You want to divide it into servings of 1 ⅓ pizzas each. How many servings can you make? Intuitively, you can't make even one full serving, as a serving is larger than the pizza itself. The answer, ¾, tells us that you can make ¾ of a serving. This visual representation reinforces the mathematical solution.
The Importance of Understanding Fraction Division
Mastering fraction division is crucial for various mathematical applications, including:
- Algebra: Many algebraic equations involve fractions, requiring a solid understanding of fraction operations.
- Geometry: Calculating areas and volumes of shapes often involves fraction calculations.
- Calculus: The foundations of calculus rely heavily on the concepts of limits and derivatives, which often involve fractions.
- Real-world applications: From baking (measuring ingredients) to construction (measuring materials), fraction division is essential in everyday life.
Exploring Further: Division with Different Fractions
Let's expand our understanding by looking at a few more examples of fraction division:
Example 1: 2 ÷ ½
- Convert to improper fractions (if necessary): 2 can be expressed as ²⁄₁.
- Change division to multiplication and use the reciprocal: ²⁄₁ x ²⁄₁
- Multiply: 2 x 2 = 4 and 1 x 1 = 1
- Simplify: The result is ⁴⁄₁ which simplifies to 4.
Therefore, 2 ÷ ½ = 4.
Example 2: ¾ ÷ ⅔
- Convert to improper fractions (already in improper fraction): ¾ and ⅔
- Change division to multiplication and use the reciprocal: ¾ x ³⁄₂
- Multiply: 3 x 3 = 9 and 4 x 2 = 8
- Simplify: The result is ⁹⁄₈ which can also be expressed as 1⅛.
Therefore, ¾ ÷ ⅔ = ⁹⁄₈ or 1⅛.
Frequently Asked Questions (FAQs)
Q: Why do we use the reciprocal when dividing fractions?
A: Using the reciprocal is a mathematical shortcut that simplifies the process. Dividing by a fraction is equivalent to multiplying by its reciprocal. This method avoids the complexity of finding a common denominator, which is the traditional approach.
Q: What if the result of the fraction division is an improper fraction?
A: If you obtain an improper fraction as a result, you can convert it back into a mixed number for easier understanding. This is done by dividing the numerator by the denominator. The quotient becomes the whole number, and the remainder becomes the numerator of the fraction, keeping the same denominator.
Q: Can I use a calculator for fraction division?
A: Yes, most scientific calculators have the functionality to perform fraction division directly. However, understanding the underlying mathematical principles remains crucial for solving more complex problems.
Q: Are there any alternative methods for dividing fractions?
A: While the reciprocal method is the most efficient and widely used, you can also use the traditional method of finding a common denominator and then dividing the numerators. However, the reciprocal method is generally faster and easier.
Conclusion: Mastering Fractions, One Step at a Time
Dividing 1 by 1 ⅓, although seemingly straightforward, provides a valuable opportunity to reinforce our understanding of fractions and their operations. By mastering fraction division, you unlock a critical skill applicable to various mathematical disciplines and real-world scenarios. Remember to break down complex problems into smaller, manageable steps, and don't hesitate to practice regularly. With consistent effort and a clear understanding of the concepts, you will confidently navigate the world of fractions and their myriad applications. The journey of mathematical understanding is a rewarding one, filled with the satisfaction of solving intricate problems and appreciating the elegant logic of numbers. Keep exploring, keep learning, and keep solving!
Latest Posts
Latest Posts
-
Map Of Pacific Northwest Region
Sep 02, 2025
-
All The Pretty Horses Lyrics
Sep 02, 2025
-
Corn Parts Of The Plant
Sep 02, 2025
-
Olivia From The Twelfth Night
Sep 02, 2025
-
Tea Tree Oil In Spanish
Sep 02, 2025
Related Post
Thank you for visiting our website which covers about 1 Divided By 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.