1 8 As A Percentage
scising
Sep 11, 2025 · 5 min read
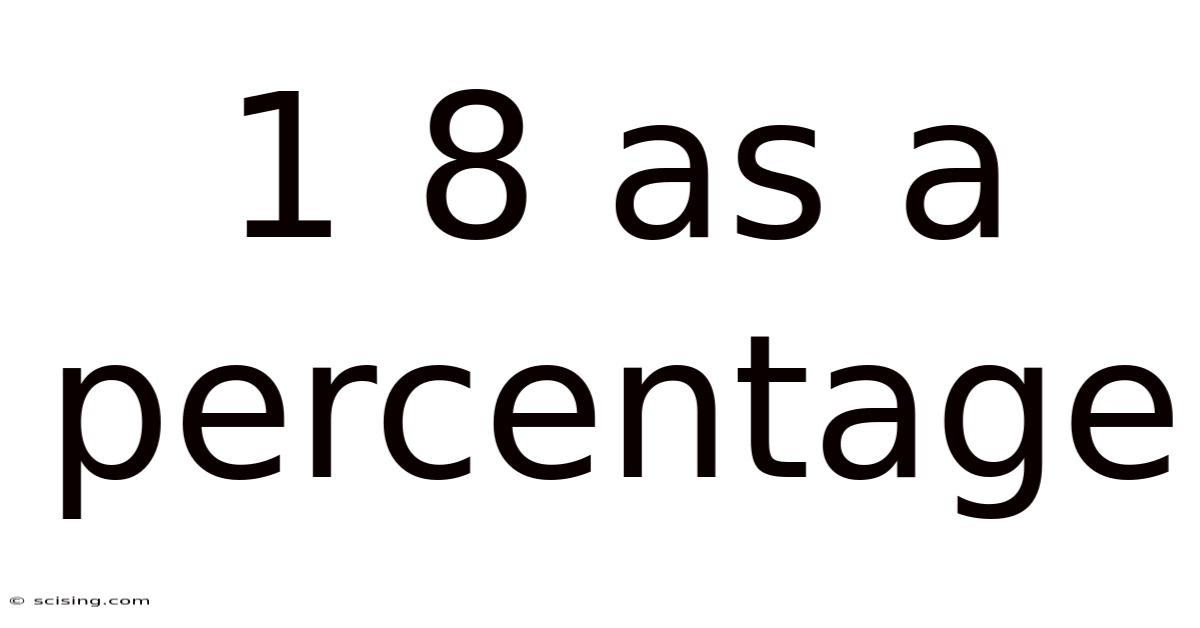
Table of Contents
Understanding 1/8 as a Percentage: A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts to understanding financial reports. This comprehensive guide will explore the concept of 1/8 as a percentage, providing a detailed explanation, step-by-step calculations, and addressing frequently asked questions. We'll delve into the underlying principles, ensuring a thorough understanding for learners of all levels.
Introduction: Fractions, Decimals, and Percentages
Before we dive into the specifics of 1/8, let's establish a clear understanding of the relationship between fractions, decimals, and percentages. These three represent different ways of expressing parts of a whole. A fraction expresses a part of a whole as a ratio of two numbers (numerator/denominator). A decimal expresses a part of a whole using base-ten notation, where a decimal point separates the whole number from the fractional part. A percentage expresses a part of a whole as a fraction of 100. These three forms are interchangeable, meaning you can convert one to the other without changing the value.
Converting 1/8 to a Decimal
The first step in converting 1/8 to a percentage is to convert it to a decimal. This is done by dividing the numerator (1) by the denominator (8):
1 ÷ 8 = 0.125
Therefore, 1/8 is equivalent to 0.125.
Converting the Decimal to a Percentage
To convert the decimal 0.125 to a percentage, we multiply it by 100 and add the percentage sign (%):
0.125 × 100 = 12.5
Therefore, 0.125 is equivalent to 12.5%.
Combining the Steps: 1/8 as a Percentage
Combining the steps above, we can directly convert 1/8 to a percentage as follows:
- Divide the numerator by the denominator: 1 ÷ 8 = 0.125
- Multiply the result by 100: 0.125 × 100 = 12.5
- Add the percentage sign: 12.5%
Therefore, 1/8 is equal to 12.5%.
Visual Representation of 1/8
Visualizing fractions can significantly aid in understanding. Imagine a circle divided into 8 equal slices. 1/8 represents one of these slices. If you were to represent the entire circle as 100%, then one slice (1/8) would represent 12.5% of the whole. Similarly, you can visualize this with a rectangle, a bar graph, or any other shape divided into 8 equal parts. This visual approach helps solidify the concept and makes it more intuitive.
Real-World Applications of 1/8 as a Percentage
Understanding 1/8 as 12.5% has numerous practical applications:
- Discounts: A store offering an 1/8 discount on an item is offering a 12.5% discount.
- Sales Tax: If a sales tax is 1/8, then the tax added to the price is 12.5%.
- Proportions: If a recipe calls for 1/8 cup of sugar, you can think of it as using 12.5% of a cup.
- Data Analysis: In data analysis, understanding proportions and percentages is crucial. Representing a portion of data as 1/8 provides a clearer context when the entire dataset is considered.
- Financial Calculations: From calculating interest rates to understanding loan repayments, percentage conversions are vital. Knowing that 1/8 is 12.5% allows for quicker and more accurate financial calculations.
Different Methods for Calculating Percentages
While the method outlined above is the most straightforward, several other methods can be used to convert fractions to percentages. These include:
- Using Proportions: You can set up a proportion: 1/8 = x/100. Solving for x will give you the percentage equivalent.
- Using a Calculator: Most calculators have a percentage function that can directly convert fractions to percentages. Simply enter the fraction as a division (1 ÷ 8) and then multiply by 100.
Expanding the Concept: Other Fractions and Percentages
Understanding the conversion of 1/8 to a percentage provides a foundation for understanding other fraction-to-percentage conversions. The principle remains the same: divide the numerator by the denominator and multiply the result by 100. For example:
- 1/4 = 0.25 = 25%
- 1/2 = 0.5 = 50%
- 3/4 = 0.75 = 75%
- 1/10 = 0.1 = 10%
- 1/100 = 0.01 = 1%
Frequently Asked Questions (FAQ)
-
Q: What is 1/8 expressed as a decimal?
- A: 1/8 expressed as a decimal is 0.125.
-
Q: How do I convert a fraction to a percentage?
- A: To convert a fraction to a percentage, divide the numerator by the denominator and multiply the result by 100. Add a "%" sign to indicate the percentage.
-
Q: Is there a shortcut for converting 1/8 to a percentage?
- A: While the direct method is always reliable, you can memorize that 1/8 equals 12.5%.
-
Q: What are some real-world examples of using 1/8 as a percentage?
- A: Real-world examples include calculating discounts, sales tax, proportions in recipes, and interpreting data in various fields.
-
Q: What if I need to calculate a percentage of a larger number using 1/8?
- A: Multiply the number by 0.125 (or 12.5%). For example, 1/8 of 160 is 160 x 0.125 = 20.
Conclusion: Mastering Fraction-to-Percentage Conversions
Understanding the conversion of fractions to percentages, especially simple fractions like 1/8, is a crucial mathematical skill. The ability to quickly and accurately perform these conversions enhances problem-solving capabilities in various contexts – from everyday scenarios to complex mathematical applications. By grasping the underlying principles and practicing regularly, you'll develop a strong foundation in this important area of mathematics. Remember to visualize the fractions and practice converting different fractions to percentages to solidify your understanding. This will not only improve your mathematical skills but also boost your confidence in tackling various numerical challenges. Mastering this seemingly simple concept unlocks a deeper understanding of the relationships between fractions, decimals, and percentages, paving the way for more advanced mathematical concepts.
Latest Posts
Latest Posts
-
Simple Trust Vs Complex Trust
Sep 11, 2025
-
Finding Cubic Equation Residual Equation
Sep 11, 2025
-
49 Weeks Ago From Today
Sep 11, 2025
-
Starry Night And The Astronauts
Sep 11, 2025
-
How Many Inches Is 35cm
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 1 8 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.