1 4 Divided By 5
scising
Sep 18, 2025 · 5 min read
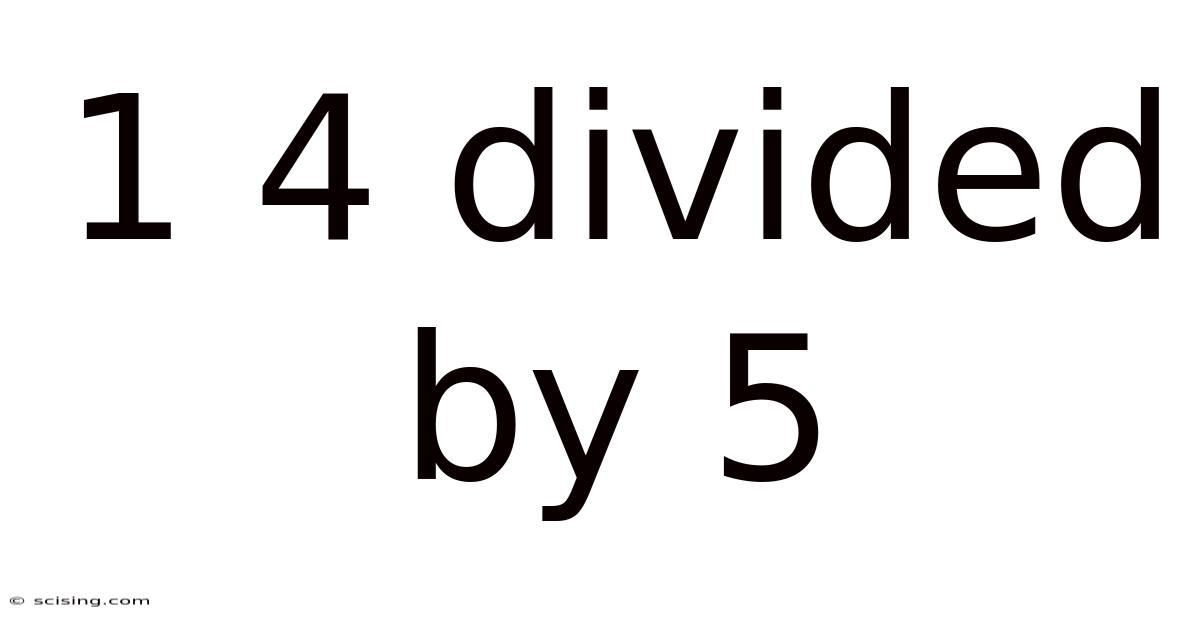
Table of Contents
Unpacking 1/4 Divided by 5: A Deep Dive into Fraction Division
Understanding fraction division can be a stumbling block for many, but it's a crucial skill in mathematics. This comprehensive guide will walk you through the process of dividing 1/4 by 5, explaining not only the mechanics but also the underlying concepts. We'll explore different approaches, offering clarity and building your confidence in tackling similar problems. By the end, you'll not only know the answer but also understand why the answer is what it is.
Introduction: Understanding the Basics of Fraction Division
Before diving into the specific problem of 1/4 divided by 5, let's review the fundamental principles of fraction division. The core concept revolves around the idea of reciprocals. The reciprocal of a fraction is simply that fraction flipped upside down. For example, the reciprocal of 2/3 is 3/2. Dividing by a fraction is the same as multiplying by its reciprocal. This principle simplifies the process significantly.
Remember that any whole number can be expressed as a fraction with a denominator of 1. Therefore, 5 can be written as 5/1. This representation will be crucial when we tackle our problem.
Method 1: Using the Reciprocal
This is arguably the most straightforward method for dividing fractions. Let's apply it to our problem: 1/4 ÷ 5.
-
Rewrite the whole number as a fraction: 5 becomes 5/1. Our problem now looks like this: 1/4 ÷ 5/1.
-
Replace division with multiplication by the reciprocal: Instead of dividing by 5/1, we multiply by its reciprocal, which is 1/5. The equation becomes: 1/4 x 1/5.
-
Multiply the numerators and the denominators: Multiply the top numbers (numerators) together: 1 x 1 = 1. Then, multiply the bottom numbers (denominators) together: 4 x 5 = 20.
-
Simplify the result: The resulting fraction is 1/20. This fraction is already in its simplest form, meaning there are no common factors between the numerator and denominator that can be canceled out.
Therefore, 1/4 divided by 5 is 1/20.
Method 2: Visual Representation with Area Models
Visualizing fractions can significantly improve understanding. Let's use an area model to represent 1/4 divided by 5.
Imagine a square representing one whole unit. Divide this square into four equal parts. One of these parts represents 1/4. Now, imagine dividing this 1/4 section into five equal parts. Each of these smaller sections represents 1/20 of the original whole square. This visually demonstrates that 1/4 divided into five equal parts results in 1/20.
Method 3: Thinking in Terms of Repeated Subtraction
While less efficient for this specific problem, understanding division as repeated subtraction provides a valuable alternative perspective. Dividing 1/4 by 5 means finding out how many times 1/5 goes into 1/4. Although this approach is not ideal for calculations involving fractions, it helps solidify the conceptual understanding. In essence, you're asking: "How many 1/5 pieces can I fit into 1/4 piece?" Since 1/5 is larger than 1/4, you can fit a fraction of a 1/5 piece into the 1/4 piece, leading to a fraction as a result. This is a clear indication that the result will be less than 1.
The Scientific Explanation: Why Does This Work?
The success of the reciprocal method hinges on the fundamental principles of fraction multiplication and division. When we divide by a fraction, we are essentially asking: "How many times does this fraction fit into the other?" Multiplying by the reciprocal effectively answers this question. Imagine dividing a pizza into 4 slices (1/4). If you divide each of those 1/4 slices further into five equal pieces, you have 20 total pieces (1/20 each).
Frequently Asked Questions (FAQ)
-
Q: Can I divide fractions using a calculator? A: Yes, most calculators can handle fraction division. However, understanding the underlying principles is crucial for solving more complex problems and building a strong mathematical foundation.
-
Q: What if I have a mixed number instead of a proper fraction? A: Convert the mixed number into an improper fraction before applying the reciprocal method. For example, 1 1/2 would become 3/2.
-
Q: What happens if I divide by a fraction smaller than the original fraction? A: In that case, the resulting fraction will be larger than the original fraction because you're dividing into smaller pieces, effectively increasing the number of pieces. For example, 1/4 divided by 1/8 would result in 2.
-
Q: Is there a difference between dividing a fraction by a whole number and dividing a whole number by a fraction? A: Yes. Dividing a fraction by a whole number results in a smaller fraction (as in our example), while dividing a whole number by a fraction results in a larger number (e.g., 5 divided by 1/2 = 10).
Real-world Applications: Where do we use this?
Understanding fraction division is not limited to classroom exercises; it has numerous practical applications in various fields:
- Cooking: Adjusting recipes involves scaling ingredients up or down, often requiring fraction division.
- Sewing: Calculating fabric requirements for a project often involves working with fractions and their division.
- Construction: Dividing materials like lumber or concrete accurately relies on understanding fractions and division.
- Engineering: Many engineering calculations involve precise measurements and scaling, often requiring fraction division.
Conclusion: Mastering Fraction Division
Mastering fraction division is a cornerstone of mathematical proficiency. By understanding the concept of reciprocals and applying the appropriate methods, you can confidently tackle any fraction division problem. The approaches outlined in this guide—using the reciprocal, visual representation, and even considering repeated subtraction—provide a multifaceted understanding. Remember to practice regularly, and you'll soon find yourself proficient in handling fractions with ease. Don't hesitate to revisit this guide and the underlying principles as needed. With consistent practice, fraction division will transition from a potential obstacle to a readily mastered skill. The seemingly simple problem of 1/4 divided by 5 highlights the power and beauty of fundamental mathematical concepts.
Latest Posts
Latest Posts
-
Witch Sword In The Stone
Sep 18, 2025
-
Map For The Great Gatsby
Sep 18, 2025
-
Least Common Multiple 4 12
Sep 18, 2025
-
Black Hair And Brown Eyes
Sep 18, 2025
-
How Tall Is 183 Centimeters
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 1 4 Divided By 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.