1 3 Plus 1 3
scising
Sep 06, 2025 · 6 min read
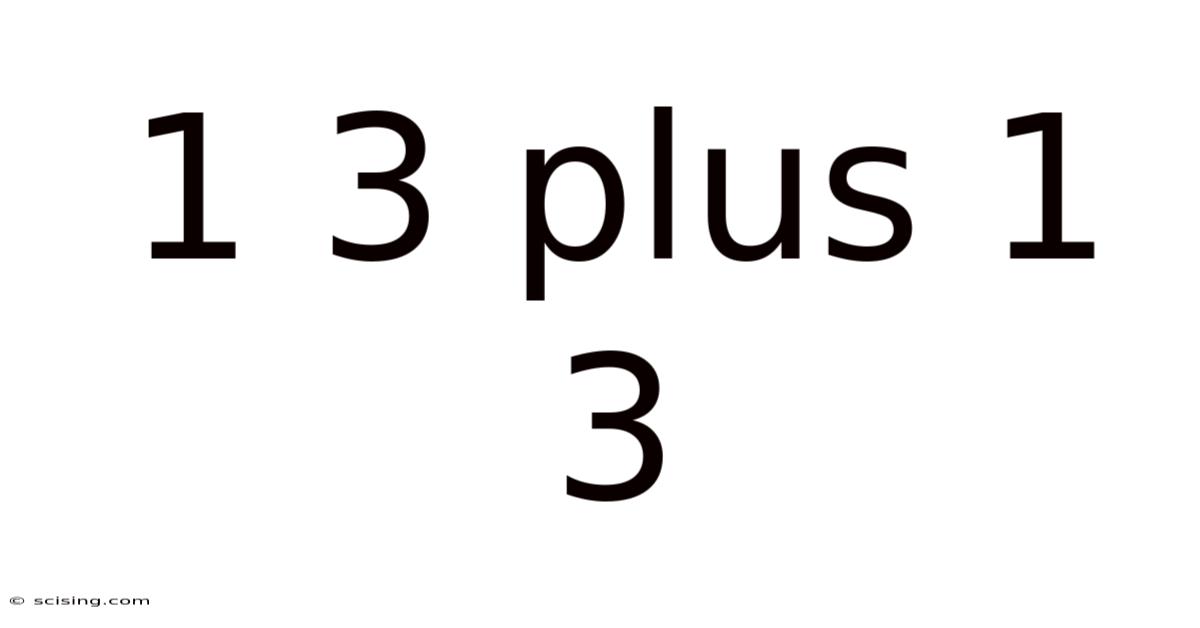
Table of Contents
Decoding 1/3 + 1/3: A Deep Dive into Fractions and Their Applications
This article explores the seemingly simple addition problem of 1/3 + 1/3, delving beyond the immediate answer to uncover the underlying principles of fractions, their practical applications, and the broader mathematical concepts they represent. Understanding fractions is fundamental to various fields, from baking and cooking to engineering and finance. This exploration aims to solidify your grasp of fractions and demonstrate their relevance in everyday life and advanced studies.
Introduction: The Foundation of Fractions
Fractions represent parts of a whole. The number on top, the numerator, indicates how many parts we have. The number on the bottom, the denominator, shows how many equal parts the whole is divided into. In the problem 1/3 + 1/3, both fractions share the same denominator (3), signifying that both parts are from the same whole, divided into three equal pieces. This common denominator is crucial for simplifying the addition process.
Solving 1/3 + 1/3: A Step-by-Step Guide
Adding fractions with a common denominator is straightforward. We simply add the numerators while keeping the denominator the same. Therefore:
1/3 + 1/3 = (1 + 1) / 3 = 2/3
The solution, 2/3, indicates that we have two out of three equal parts of the whole. This simple operation forms the basis for more complex fractional calculations.
Visualizing Fractions: A Pictorial Representation
Visual aids can significantly enhance understanding, especially when working with fractions. Imagine a circle divided into three equal slices (representing the denominator, 3). Each slice represents 1/3. If we add two of these slices (1/3 + 1/3), we visually obtain 2/3 of the entire circle. This visual representation helps solidify the concept and makes it more intuitive. Similar visualizations can be applied using rectangles, squares, or any other shape divided into equal parts.
Expanding the Concept: Adding Fractions with Different Denominators
While 1/3 + 1/3 is relatively simple due to the common denominator, adding fractions with different denominators requires an extra step – finding a common denominator. This involves finding the least common multiple (LCM) of the denominators. For example, consider adding 1/2 + 1/4:
- Find the LCM: The LCM of 2 and 4 is 4.
- Convert to equivalent fractions: 1/2 is equivalent to 2/4 (multiply both numerator and denominator by 2).
- Add the fractions: 2/4 + 1/4 = 3/4
This illustrates that adding fractions necessitates a common basis for comparison, ensuring that we are adding parts of the same whole. The concept of finding a common denominator is fundamental to mastering fraction arithmetic.
Real-World Applications: Fractions in Everyday Life
Fractions are ubiquitous in daily life, appearing in various contexts:
-
Cooking and Baking: Recipes often involve fractional measurements, like 1/2 cup of sugar or 2/3 cup of flour. Accurate measurements are essential for successful baking, highlighting the importance of understanding fractional arithmetic.
-
Measurement and Construction: Carpenters, engineers, and other tradespeople regularly use fractions in their work. Precise measurements are critical for constructing buildings, bridges, and other structures. Inaccurate fractional calculations can have significant consequences.
-
Finance and Economics: Fractions are essential in finance, representing portions of investments, interest rates, and other financial metrics. Understanding fractions is crucial for making sound financial decisions.
-
Time Management: Fractions are often used to represent parts of an hour, like 1/4 hour (15 minutes) or 1/2 hour (30 minutes). Effective time management relies on accurate estimations and calculations involving fractions.
Beyond Addition: Subtraction, Multiplication, and Division of Fractions
While this article focuses on addition, it's important to understand that fractions also involve subtraction, multiplication, and division.
-
Subtraction: Similar to addition, subtracting fractions with a common denominator involves subtracting the numerators while keeping the denominator the same. If the denominators differ, we must first find a common denominator before subtraction.
-
Multiplication: Multiplying fractions is simpler than addition or subtraction. We multiply the numerators together and then multiply the denominators together. For example, (1/3) * (2/5) = 2/15.
-
Division: Dividing fractions involves inverting the second fraction (the divisor) and then multiplying. For instance, (1/3) ÷ (2/5) = (1/3) * (5/2) = 5/6.
Understanding Equivalent Fractions: Simplifying and Expanding
Equivalent fractions represent the same value but are expressed differently. For example, 1/2, 2/4, and 3/6 are all equivalent fractions. Simplifying fractions involves reducing them to their lowest terms by dividing both the numerator and denominator by their greatest common divisor (GCD). Expanding fractions involves multiplying both the numerator and denominator by the same number. This process is crucial for comparing and adding fractions with different denominators.
Decimal Equivalents: The Relationship Between Fractions and Decimals
Fractions can be expressed as decimals by dividing the numerator by the denominator. For instance, 1/3 is approximately 0.333... (a recurring decimal). Understanding this relationship allows for flexible calculations and conversions between fractional and decimal forms. This is particularly useful when working with calculators or computers, which often operate using decimal representations.
Advanced Applications: Fractions in Algebra and Calculus
Fractions form the foundation for more advanced mathematical concepts. In algebra, they appear in equations and expressions, and manipulating fractions is critical for solving algebraic problems. In calculus, fractions are fundamental in concepts like derivatives and integrals, where understanding fractional operations is crucial for solving complex problems.
Addressing Common Mistakes: Pitfalls to Avoid
Common mistakes when working with fractions include:
-
Incorrectly adding or subtracting numerators and denominators: Remember, only the numerators are added or subtracted when the denominators are the same. The denominator remains unchanged.
-
Forgetting to find a common denominator: This is a frequent error when adding or subtracting fractions with different denominators. Always ensure you have a common denominator before proceeding with the calculation.
-
Incorrect simplification: Make sure to simplify fractions to their lowest terms by dividing both the numerator and denominator by their GCD.
-
Mistakes in multiplication and division: Carefully follow the rules for multiplying and dividing fractions to avoid errors.
Frequently Asked Questions (FAQ)
Q: Can I add fractions with different denominators directly?
A: No, you must first find a common denominator before adding or subtracting fractions.
Q: What happens if I multiply the numerator and denominator of a fraction by the same number?
A: You create an equivalent fraction; the value of the fraction remains the same.
Q: How do I simplify a fraction?
A: Divide both the numerator and denominator by their greatest common divisor (GCD).
Q: What if the denominator is zero?
A: A fraction with a denominator of zero is undefined. Division by zero is not permitted in mathematics.
Q: Are all fractions rational numbers?
A: Yes, all fractions can be expressed as the ratio of two integers (numerator and denominator), and thus are rational numbers.
Conclusion: The Enduring Importance of Fractions
This exploration of 1/3 + 1/3 has extended beyond a simple arithmetic problem to reveal the profound significance of fractions in mathematics and their widespread applicability in various fields. From everyday tasks like cooking to complex scientific calculations, a solid understanding of fractions is invaluable. Mastering fractions is not merely about solving equations; it's about developing a fundamental mathematical literacy that empowers you to navigate the quantitative world effectively and confidently. By understanding the underlying principles and avoiding common pitfalls, you can build a strong foundation for more advanced mathematical concepts and applications. The seemingly simple addition of 1/3 + 1/3 opens the door to a vast world of mathematical understanding and practical problem-solving.
Latest Posts
Latest Posts
-
1 Yard To Square Feet
Sep 06, 2025
-
16 Ounces In A Gallon
Sep 06, 2025
-
Anatomy Of A Tarantula Spider
Sep 06, 2025
-
Does A Circle Have Sides
Sep 06, 2025
-
How Many Inches In 13cm
Sep 06, 2025
Related Post
Thank you for visiting our website which covers about 1 3 Plus 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.