1 2 X 1 3
scising
Sep 18, 2025 · 5 min read
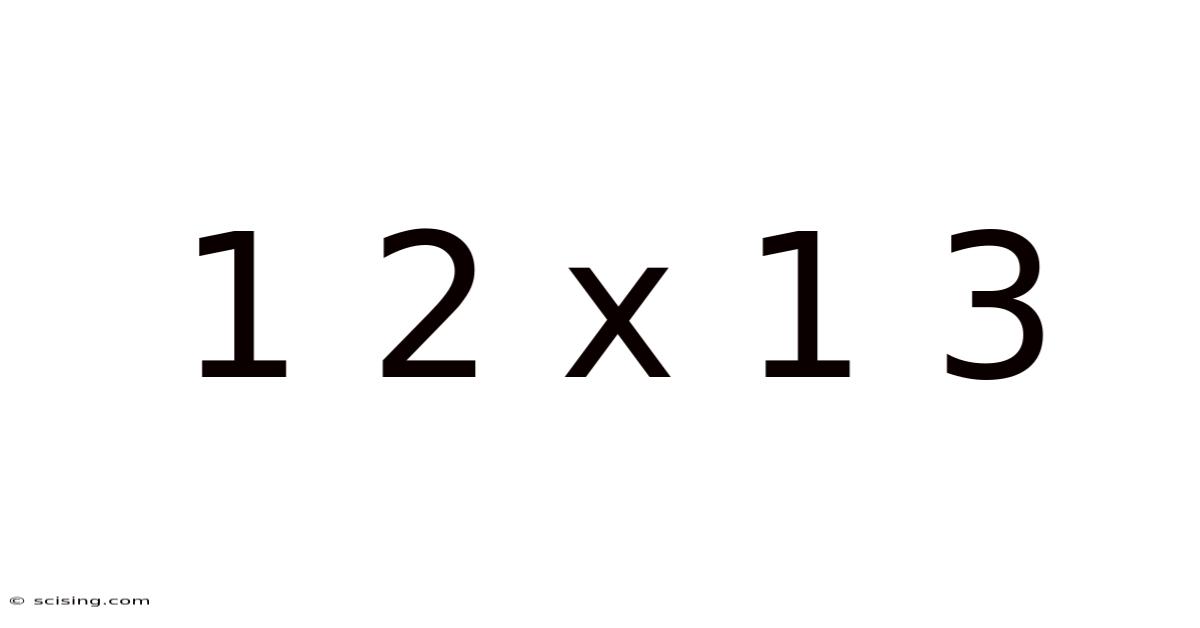
Table of Contents
Decoding 1 2 x 1 3: A Deep Dive into Multiplication and Beyond
This article delves into the seemingly simple mathematical expression "1 2 x 1 3," exploring its straightforward solution, the underlying principles of multiplication, and its applications in more complex mathematical contexts. We will also unpack the significance of understanding basic arithmetic operations and how they form the foundation for advanced mathematical concepts. This exploration is suitable for students and anyone seeking a refresher on fundamental mathematical skills and their broader implications.
Understanding the Fundamentals: Multiplication
At its core, "1 2 x 1 3" represents a multiplication problem. Multiplication is a fundamental arithmetic operation that involves repeated addition. When we say "1 2 x 1 3," we are essentially asking: "What is the result of adding 12 thirteen times, or adding 13 twelve times?" Both approaches will yield the same answer.
Solving 12 x 13:
The most straightforward method to solve this problem is through standard multiplication. We can break down the calculation as follows:
-
Step 1: Multiply 12 by 3 (the ones digit of 13): 12 x 3 = 36. We write down 6 and carry-over 3.
-
Step 2: Multiply 12 by 1 (the tens digit of 13): 12 x 1 = 12. We add the carry-over 3 from the previous step: 12 + 3 = 15. We write down 15.
-
Step 3: Combine the results: The final answer is 156.
Therefore, 12 x 13 = 156.
Beyond the Basics: Exploring Different Methods
While the standard multiplication method is efficient, understanding alternative approaches can deepen our comprehension of the underlying mathematical principles. Let's explore a few:
1. Distributive Property:
The distributive property states that a(b + c) = ab + ac. We can apply this to our problem by breaking down 13 into 10 + 3:
12 x (10 + 3) = (12 x 10) + (12 x 3) = 120 + 36 = 156
This method highlights the relationship between multiplication and addition, emphasizing that multiplication is simply a more efficient way to perform repeated addition.
2. Lattice Multiplication:
Lattice multiplication is a visual method that can be particularly helpful for larger numbers. It involves creating a grid and performing smaller multiplications within each cell before summing the results diagonally. While it might seem more complex for this specific problem, it becomes significantly more efficient when dealing with larger numbers.
3. Mental Math Techniques:
With practice, we can develop mental math techniques to quickly solve multiplication problems. For instance, we can use the fact that 12 x 10 = 120 and then add 12 x 3 = 36 to get 156. This approach combines decomposition with efficient mental arithmetic.
The Significance of Place Value
Understanding place value is crucial in correctly performing multiplication, especially with larger numbers. In the number 12, the '1' represents ten and the '2' represents two ones. Similarly, in 13, the '1' represents ten and the '3' represents three ones. The standard multiplication method implicitly accounts for place value by aligning the digits correctly and carrying over values.
Applications in Real-World Scenarios
The seemingly simple operation 12 x 13 has numerous applications in everyday life:
-
Calculating Costs: If you buy 12 items costing $13 each, the total cost would be 12 x $13 = $156.
-
Measuring Area: If a rectangular room measures 12 feet by 13 feet, its area would be 12 x 13 = 156 square feet.
-
Problem Solving: Many everyday problems, from calculating the number of tiles needed to cover a floor to determining the total distance traveled on a journey, involve multiplication.
These examples highlight how a seemingly simple mathematical operation underlies numerous practical scenarios. Mastering multiplication is essential for efficiently navigating many aspects of daily life.
Extending the Concept: Beyond Basic Multiplication
Understanding 12 x 13 lays the groundwork for more complex mathematical concepts. Let's explore a few:
1. Algebra: In algebra, we use variables to represent unknown quantities. We can express the problem as: x * y = z, where x = 12, y = 13, and z = 156. This introduction of variables allows us to solve for unknown values in various equations.
2. Geometry: The area of a rectangle is calculated using the formula: Area = length x width. Our problem 12 x 13 directly relates to calculating the area of a rectangle with dimensions 12 units by 13 units.
3. Calculus: While seemingly distant from basic multiplication, calculus utilizes the concept of limits and derivatives, which build upon the foundational understanding of arithmetic operations.
4. Number Theory: Understanding prime factorization and divisibility rules builds upon the core concepts involved in multiplication. For example, understanding the prime factorization of 12 (2 x 2 x 3) and 13 (13) helps in understanding the factors of their product.
Frequently Asked Questions (FAQ)
Q: What if the numbers were larger? How would I solve it?
A: For larger numbers, the standard long multiplication method, lattice multiplication, or a calculator remain effective tools. The core principles of place value and carrying remain the same.
Q: Are there any tricks to make multiplication easier?
A: Yes! Many mental math tricks exist. Practicing multiplication tables, understanding the distributive property, and recognizing patterns are all valuable techniques to improve speed and efficiency.
Q: Why is it important to learn multiplication?
A: Multiplication is a fundamental building block of mathematics. A strong grasp of multiplication is essential for success in algebra, geometry, and other advanced mathematical fields. Moreover, it's crucial for everyday problem-solving and managing finances.
Q: How can I improve my multiplication skills?
A: Consistent practice is key! Use flashcards, online games, and work through various problems to build proficiency. Understanding different methods and finding the approach that works best for you is also crucial.
Conclusion: Mastering the Fundamentals for Future Success
The seemingly simple problem of "1 2 x 1 3" provides a gateway to understanding a vast landscape of mathematical concepts. From basic arithmetic to advanced algebraic and geometric applications, mastering fundamental operations like multiplication is paramount for success in mathematics and numerous real-world scenarios. By exploring different methods and understanding the underlying principles, we can not only solve this specific problem but also develop a stronger mathematical foundation for future learning and problem-solving. Remember that consistent practice and a curious mindset are key to unlocking the full potential of mathematical concepts, no matter how seemingly simple they may appear initially. Continue to explore, question, and challenge yourself – the world of mathematics awaits!
Latest Posts
Latest Posts
-
Hearth Definition Ap Human Geography
Sep 18, 2025
-
The 4 Seasons In Spanish
Sep 18, 2025
-
How Much Is 40 Ounces
Sep 18, 2025
-
The Robe Lloyd C Douglas
Sep 18, 2025
-
Silence Of The Lamb Book
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 1 2 X 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.