1 2/3 + 1 2/3
scising
Sep 15, 2025 · 6 min read
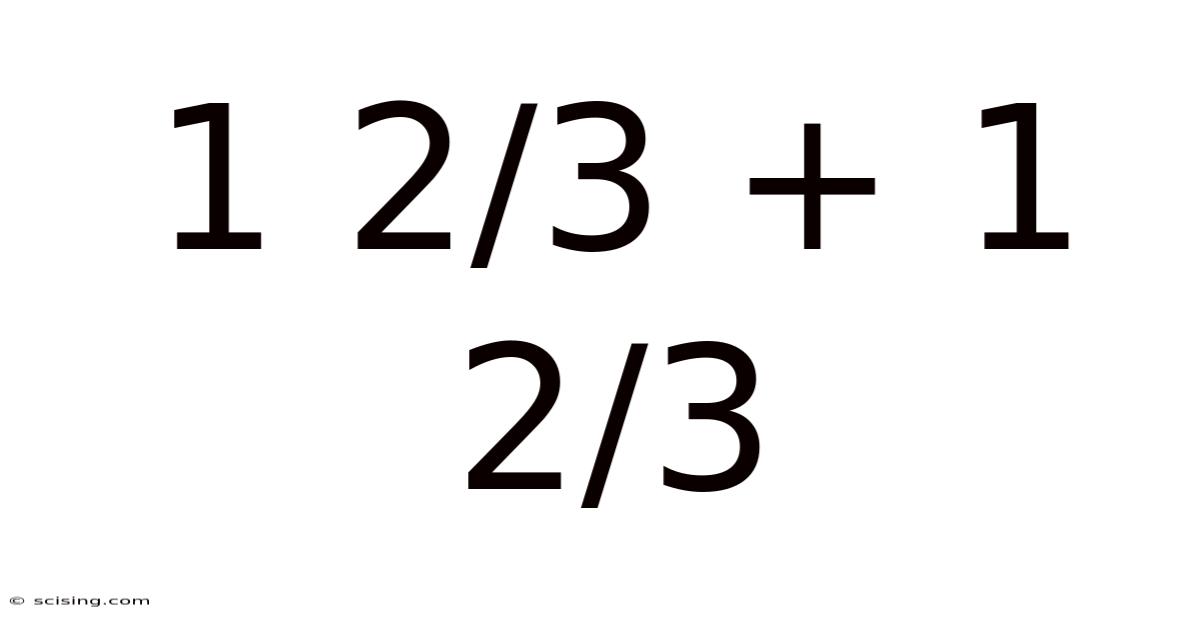
Table of Contents
Decoding 1 2/3 + 1 2/3: A Deep Dive into Fraction Addition
Adding fractions might seem like a simple task, especially when dealing with seemingly straightforward numbers like 1 2/3. However, understanding the underlying principles of fraction addition is crucial for building a strong foundation in mathematics. This article will not only guide you through solving 1 2/3 + 1 2/3 but will also delve into the core concepts, offering a comprehensive understanding that extends far beyond this specific problem. We will explore different methods, explain the reasoning behind each step, and address common misconceptions. This is more than just an answer; it's a journey into the world of fractions.
Understanding Fractions: A Quick Refresher
Before tackling the addition problem, let's ensure we're all on the same page regarding fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator tells us how many equal parts the whole is divided into, while the numerator indicates how many of those parts we're considering.
For example, in the fraction 2/3, the denominator (3) means the whole is divided into three equal parts, and the numerator (2) signifies that we're considering two of those parts.
Mixed numbers, like 1 2/3, combine a whole number with a fraction. 1 2/3 means we have one whole unit and two-thirds of another unit.
Method 1: Converting to Improper Fractions
This is a common and highly effective method for adding mixed numbers. The process involves converting each mixed number into an improper fraction, where the numerator is larger than the denominator.
Step 1: Convert 1 2/3 to an improper fraction.
To do this, we multiply the whole number (1) by the denominator (3), and then add the numerator (2). This result becomes the new numerator, while the denominator remains the same.
1 x 3 + 2 = 5
Therefore, 1 2/3 becomes 5/3.
Step 2: Repeat for the second mixed number.
Since we are adding 1 2/3 + 1 2/3, we repeat the process for the second mixed number, which also results in 5/3.
Step 3: Add the improper fractions.
Now we add the two improper fractions: 5/3 + 5/3. Because the denominators are the same, we simply add the numerators: 5 + 5 = 10. The denominator stays the same.
This gives us 10/3.
Step 4: Convert back to a mixed number (if needed).
The answer 10/3 is an improper fraction. To convert it back to a mixed number, we divide the numerator (10) by the denominator (3).
10 ÷ 3 = 3 with a remainder of 1.
This means we have 3 whole units and 1/3 of another unit. Therefore, the final answer is 3 1/3.
Method 2: Adding the Whole Numbers and Fractions Separately
This method involves adding the whole numbers and the fractional parts separately, then combining the results.
Step 1: Add the whole numbers.
In 1 2/3 + 1 2/3, we add the whole numbers: 1 + 1 = 2.
Step 2: Add the fractions.
Next, we add the fractions: 2/3 + 2/3 = 4/3.
Step 3: Simplify the fractional part.
4/3 is an improper fraction. We convert it to a mixed number: 4 ÷ 3 = 1 with a remainder of 1. So, 4/3 becomes 1 1/3.
Step 4: Combine the whole number and fractional parts.
Finally, we combine the results from steps 1 and 3: 2 + 1 1/3 = 3 1/3.
Therefore, the answer is again 3 1/3.
Visual Representation: Understanding the Solution
It's helpful to visualize this addition problem. Imagine you have two pizzas, each cut into three equal slices. 1 2/3 represents one whole pizza and two-thirds of another. Adding another 1 2/3 means adding another whole pizza and two more thirds. In total, you'd have three whole pizzas and one-third of a pizza left over, confirming our answer of 3 1/3.
The Importance of Common Denominators: A Deeper Look
Both methods above highlight the importance of common denominators when adding fractions. In our problem, the denominators were already the same (3), making the addition straightforward. However, if the denominators were different, we would need to find a common denominator before adding. A common denominator is a number that is a multiple of both denominators.
For example, if we were adding 1/2 + 1/3, we would need to find a common denominator for 2 and 3. The least common multiple of 2 and 3 is 6. We would then convert 1/2 to 3/6 and 1/3 to 2/6, and add them: 3/6 + 2/6 = 5/6.
Extending the Knowledge: Working with More Complex Fractions
The principles we've explored here apply to adding any fractions, regardless of their complexity. The key steps remain the same:
- Convert mixed numbers to improper fractions (if necessary).
- Find a common denominator (if necessary).
- Add the numerators.
- Keep the common denominator.
- Simplify the resulting fraction (convert back to a mixed number if needed).
This approach allows you to tackle problems involving larger numbers, different denominators, and even more complex mixed numbers with confidence.
Frequently Asked Questions (FAQ)
Q: Why is it important to convert mixed numbers to improper fractions before adding?
A: Converting to improper fractions simplifies the addition process. Adding the whole numbers and fractional parts separately can sometimes be more prone to errors, especially with more complex numbers. Working solely with improper fractions ensures a consistent and less error-prone approach.
Q: What if the denominators are not the same?
A: If the denominators are different, you must find a common denominator before adding the fractions. The easiest way to do this is to find the least common multiple (LCM) of the denominators.
Q: Can I add fractions directly without converting to improper fractions?
A: While you can add the whole numbers and fractional parts separately, it’s often easier and less error-prone to convert mixed numbers to improper fractions first, especially when dealing with more complex calculations. The improper fraction method provides a more streamlined and consistent approach.
Q: How can I check my answer?
A: You can check your answer by using a calculator or by reversing the process. Convert your final answer back into an improper fraction and then back into two mixed numbers to ensure that they add up to your original calculation.
Conclusion: Mastering Fraction Addition
Adding fractions, even seemingly simple ones like 1 2/3 + 1 2/3, offers a valuable opportunity to solidify your understanding of fundamental mathematical concepts. By mastering the techniques outlined in this article, you will not only be able to solve this specific problem but will also develop a strong foundation for tackling more complex fraction-related calculations in the future. Remember, the key lies in understanding the underlying principles – converting to improper fractions, finding common denominators, and simplifying the results. With practice and consistent application of these methods, you'll confidently navigate the world of fractions and their various applications. The ability to confidently manipulate fractions is a cornerstone of mathematical proficiency, opening doors to a deeper understanding of various mathematical concepts and real-world applications.
Latest Posts
Latest Posts
-
Algebra 2 Practice Questions Regents
Sep 15, 2025
-
Is Kilograms More Than Grams
Sep 15, 2025
-
Spanish For Do You Want
Sep 15, 2025
-
Amazing Grace Lyrics Original Pdf
Sep 15, 2025
-
Is Zero A Perfect Square
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 1 2/3 + 1 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.