1 000 Divided By 5
scising
Sep 22, 2025 · 6 min read
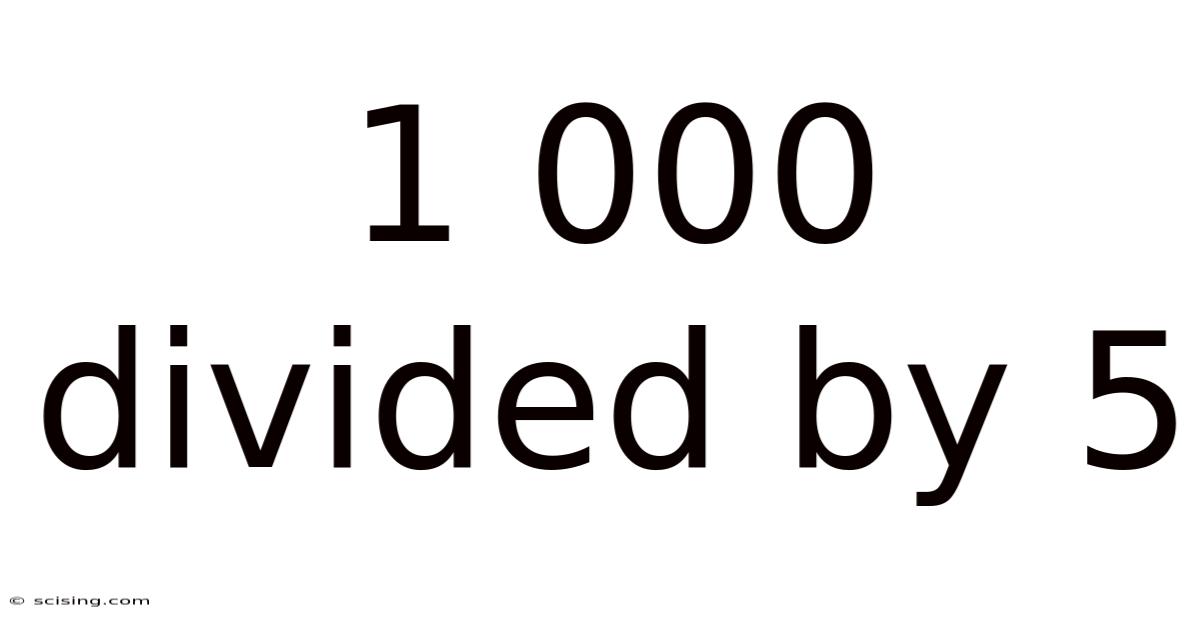
Table of Contents
1,000 Divided by 5: A Deep Dive into Division and its Applications
This article explores the seemingly simple calculation of 1,000 divided by 5, going beyond the basic answer to delve into the underlying principles of division, its various methods, real-world applications, and its significance in mathematics and beyond. We'll examine different approaches to solving this problem, exploring both mental math techniques and the formal process of long division, making this concept accessible to learners of all levels. Understanding this seemingly simple calculation opens doors to a broader appreciation of mathematical concepts and problem-solving strategies.
Understanding Division: The Basics
Division is one of the four fundamental arithmetic operations, alongside addition, subtraction, and multiplication. It essentially involves splitting a quantity into equal parts or groups. In the equation 1,000 ÷ 5 (or 1000/5), we're asking: "How many times does 5 go into 1,000?" The answer, or quotient, represents the size of each equal group when 1,000 is divided into 5 equal parts. The number being divided (1,000) is called the dividend, and the number we're dividing by (5) is the divisor.
Method 1: Mental Math – Leveraging Number Sense
For simpler division problems like 1,000 ÷ 5, mental math can be surprisingly efficient. We can use our knowledge of multiplication facts to solve this quickly. Since 5 x 200 = 1,000, we know that 1,000 divided by 5 is 200. This method relies on recognizing the relationship between multiplication and division; they are inverse operations. If we know that 5 multiplied by a number equals 1,000, then dividing 1,000 by 5 will give us that same number.
Method 2: Long Division – A Step-by-Step Approach
Long division provides a systematic method for tackling more complex division problems. While seemingly unnecessary for 1,000 ÷ 5, understanding the process is crucial for tackling larger and more intricate divisions. Here's how it works:
-
Set up the problem: Write the dividend (1,000) inside the long division symbol (⟌) and the divisor (5) outside.
-
Divide the first digit: Since 5 doesn't go into 1, we consider the first two digits, 10. 5 goes into 10 two times (5 x 2 = 10). Write the '2' above the '0' in 1,000.
-
Multiply and subtract: Multiply the quotient digit (2) by the divisor (5): 2 x 5 = 10. Subtract this result from the first two digits of the dividend: 10 - 10 = 0.
-
Bring down the next digit: Bring down the next digit from the dividend (the next '0').
-
Repeat the process: We now have '00'. 5 goes into 0 zero times. Write a '0' above the next '0' in 1000. Multiply and subtract: 0 x 5 = 0; 0 - 0 = 0.
-
Bring down the last digit: Bring down the last digit (the final '0').
-
Final division: We have '00'. 5 goes into 0 zero times. Write a '0' above the last '0' in 1000. Multiply and subtract: 0 x 5 = 0; 0 - 0 = 0.
The final answer, read from the top, is 200.
Method 3: Repeated Subtraction
This method involves repeatedly subtracting the divisor (5) from the dividend (1,000) until the remainder is 0. Each subtraction represents one group of 5. While less efficient for larger numbers, it visually demonstrates the concept of division as repeated subtraction. You would subtract 5 from 1000, then 5 from the result, and so on, until you reach 0. The number of times you subtracted 5 would be your answer (200).
Real-World Applications of Division
Division is a fundamental concept with countless applications in everyday life and various fields:
-
Sharing equally: Dividing a pizza among friends, candy among siblings, or tasks among team members. Our problem of dividing 1,000 equally amongst 5 groups directly relates to such scenarios.
-
Calculating averages: Determining average scores, speeds, temperatures, or any data set involving multiple values. The average is calculated by summing the values and dividing by the number of values.
-
Scaling recipes: Adjusting ingredient quantities in cooking or baking based on the number of servings required.
-
Financial calculations: Dividing total costs by the number of items, calculating unit prices, determining profit margins, or splitting bills.
-
Engineering and science: Division plays a critical role in various scientific calculations, including calculating speeds, densities, concentrations, and more.
Understanding Remainders
While 1,000 divided by 5 results in a whole number (200), not all divisions yield whole number quotients. Sometimes, a remainder is left over. For example, if we divide 1,003 by 5:
- 5 goes into 10 two times (5 x 2 = 10).
- Subtracting 10 from 10 leaves 0.
- Bringing down the 3, 5 goes into 3 zero times.
- The remainder is 3.
Therefore, 1,003 ÷ 5 = 200 with a remainder of 3. This remainder indicates that after forming 200 groups of 5, we have 3 left over that cannot be evenly distributed. Remainders are important in various real-world scenarios, such as determining leftover materials or calculating partial quantities.
Division in Different Number Systems
While we've focused on the decimal (base-10) number system, division operates similarly in other number systems, such as binary (base-2) or hexadecimal (base-16). The underlying principles remain consistent, though the specific calculations might vary depending on the base.
Advanced Concepts Related to Division
Understanding division opens the door to exploring more advanced mathematical concepts:
-
Fractions and decimals: Division can be represented as fractions (1000/5) and decimals (200.0).
-
Algebra: Division plays a significant role in solving algebraic equations and simplifying expressions.
-
Calculus: Differential and integral calculus involves numerous instances of division and limits, foundational for understanding change and accumulation.
Frequently Asked Questions (FAQ)
-
Q: What is the simplest way to divide 1,000 by 5?
- A: The simplest way is using mental math, recognizing that 5 x 200 = 1,000. Therefore, 1,000 ÷ 5 = 200.
-
Q: What if the dividend isn't a multiple of the divisor?
- A: If the dividend isn't a multiple of the divisor, there will be a remainder. The answer can be expressed as a whole number with a remainder or as a decimal or fraction.
-
Q: Why is understanding long division important, even for simple problems?
- A: Long division provides a systematic and adaptable method that is crucial for solving more complex division problems involving larger numbers and decimals. It strengthens mathematical understanding and problem-solving skills.
-
Q: Are there other methods besides long division and mental math?
- A: Yes, repeated subtraction is another method, although less efficient for larger numbers.
Conclusion
The seemingly straightforward calculation of 1,000 divided by 5 provides a gateway to exploring fundamental mathematical principles and their widespread applications. Whether using mental math, long division, or repeated subtraction, the process reinforces the interconnectedness of arithmetic operations and highlights the practical relevance of division in numerous aspects of life. Mastering division is not just about getting the right answer; it's about developing a deeper understanding of numerical relationships and problem-solving strategies that are essential for academic and professional success. The ability to approach this seemingly simple problem in multiple ways showcases the flexibility and power of mathematical thinking.
Latest Posts
Latest Posts
-
Economy In New Jersey Colony
Sep 22, 2025
-
The Crucible Who Is Tituba
Sep 22, 2025
-
Gone With The Wind Quotes
Sep 22, 2025
-
How To Find Bulk Density
Sep 22, 2025
-
12 Is What Of 200
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 1 000 Divided By 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.