1 000 Divided By 10
scising
Sep 23, 2025 · 6 min read
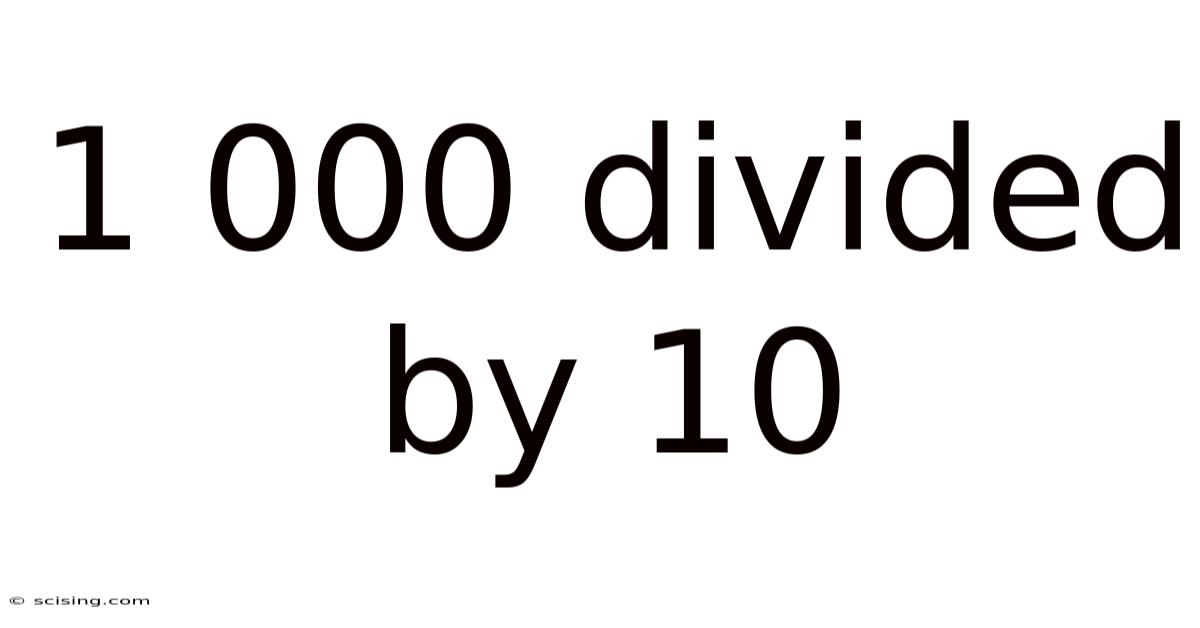
Table of Contents
1,000 Divided by 10: A Deep Dive into Division and its Applications
This article explores the seemingly simple calculation of 1,000 divided by 10, delving far beyond the answer itself. We'll unpack the fundamental concepts of division, explore various methods for solving this problem, and examine its practical applications across numerous fields. Understanding this basic operation is crucial for building a solid foundation in mathematics and problem-solving. Whether you're a student looking to solidify your understanding of division or a curious individual seeking a deeper appreciation for mathematical principles, this guide provides a comprehensive and engaging exploration.
Introduction: The Fundamentals of Division
Division is one of the four fundamental arithmetic operations, alongside addition, subtraction, and multiplication. It represents the process of splitting a quantity into equal parts. The equation "1,000 divided by 10" can be represented in several ways:
- 1000 ÷ 10
- 1000 / 10
- 1000/10
- ¹⁰⁰⁰⁄₁₀
In this case, 1,000 is the dividend (the number being divided), and 10 is the divisor (the number by which we are dividing). The result, which we'll calculate shortly, is called the quotient.
The basic concept behind division is to determine how many times the divisor fits into the dividend. In our example, we're asking: "How many times does 10 fit into 1,000?"
Calculating 1,000 Divided by 10: Multiple Approaches
There are several ways to solve 1,000 ÷ 10, each offering a different perspective on the underlying mathematics:
1. Long Division:
While seemingly cumbersome for this specific problem, long division provides a systematic approach suitable for more complex divisions.
100
10 | 1000
-10
00
0
0
0
This shows that 10 goes into 1000 exactly 100 times.
2. Repeated Subtraction:
This method involves repeatedly subtracting the divisor from the dividend until the remainder is zero. Each subtraction represents one instance of the divisor fitting into the dividend. While inefficient for large numbers, it conceptually clarifies the meaning of division.
1000 - 10 = 990 990 - 10 = 980 ...and so on until you reach 0. You would have subtracted 10 a total of 100 times.
3. Using Multiplication:
Division and multiplication are inverse operations. To find the quotient of 1000 ÷ 10, we can ask: "What number multiplied by 10 equals 1,000?" The answer, obviously, is 100.
4. Mental Math and Place Value:
Understanding place value significantly simplifies this calculation. 1,000 is 10 x 10 x 10 (10 cubed), or 100 tens. Therefore, dividing 1,000 by 10 means removing one of those tens, resulting in 100. This method highlights the relationship between powers of 10 and division.
The Answer and its Significance: 100
The quotient of 1,000 divided by 10 is 100. This seemingly simple answer underpins a vast number of calculations and real-world applications. It serves as a building block for more complex mathematical concepts and problem-solving.
Practical Applications of Division and the 1000/10 Example
The principles demonstrated by this simple division problem are used extensively across various disciplines:
1. Finance and Economics:
- Budgeting: Dividing a budget of $1,000 into 10 equal monthly installments results in $100 per month.
- Investment Returns: Calculating average annual returns on a $1,000 investment over 10 years.
- Unit Pricing: Determining the price per unit when 1,000 items cost $10,000.
2. Engineering and Physics:
- Calculating Averages: Determining the average speed of a vehicle that travels 1,000 meters in 10 seconds.
- Material Allocation: Distributing 1,000 units of a material evenly across 10 projects.
- Scaling Dimensions: Adjusting blueprint dimensions by a factor of 1/10.
3. Everyday Life:
- Sharing Resources: Evenly dividing 1,000 candies among 10 children.
- Cooking: Dividing a recipe that serves 1,000 people into smaller portions for 10 people.
- Time Management: Allocating 1,000 minutes of work over 10 days.
4. Computer Science:
- Data Processing: Dividing a large dataset into smaller chunks for efficient processing.
- Memory Allocation: Allocating 1,000 bytes of memory to 10 different processes.
- Algorithm Design: Creating algorithms that involve iterative divisions.
5. Statistics:
- Calculating Averages and Means: Dividing the sum of values by the number of values.
- Data Normalization: Scaling data to a specific range often involves division.
Understanding Remainders and Decimal Division
While 1,000 divided by 10 results in a whole number (100) with no remainder, it's important to understand how to handle remainders and decimal divisions. Consider a scenario where you divide 1,025 by 10:
1025 ÷ 10 = 102 with a remainder of 5, or 102.5
The remainder (5) indicates that 10 does not divide evenly into 1025. In decimal form, the remainder is expressed as a fraction of the divisor (5/10 = 0.5).
Beyond the Basics: Exploring More Complex Division Problems
While 1,000 divided by 10 serves as a foundational example, it’s crucial to practice with more complex problems to solidify your understanding of division. Consider these examples:
- Dividing a large number, such as 12,345,678, by a multi-digit divisor.
- Performing division with decimals.
- Utilizing division in algebraic equations.
- Working with negative numbers.
Mastering division, even at its most basic level as shown in 1000/10, lays the foundation for tackling more challenging mathematical problems and applying these concepts to a variety of real-world situations.
Frequently Asked Questions (FAQ)
Q1: What is the simplest way to calculate 1000 ÷ 10?
A1: The simplest way is to recognize that dividing by 10 is equivalent to moving the decimal point one place to the left. Since 1000 has an implied decimal point at the end, moving it one place to the left gives you 100.
Q2: Why is understanding place value important for division?
A2: Understanding place value makes division, particularly with multiples of 10, much easier. It allows you to quickly visualize the relationship between the dividend and divisor and simplifies the calculation mentally.
Q3: What happens if you divide by zero?
A3: Division by zero is undefined in mathematics. You cannot divide any number by zero. It's a fundamental rule in arithmetic.
Q4: How can I practice my division skills?
A4: Practice regularly with various problems, starting with simpler examples and gradually increasing difficulty. Use online resources, workbooks, or apps to reinforce your learning. Focus on understanding the underlying concepts rather than just memorizing procedures.
Conclusion: The Enduring Importance of a Simple Equation
The seemingly trivial calculation of 1,000 divided by 10 underscores the importance of understanding fundamental mathematical principles. While the answer—100—is straightforward, the process and its applications are far-reaching. This article aims to not only provide the solution but also to illuminate the broader significance of division within mathematics and its crucial role in solving problems across various disciplines and in everyday life. A firm grasp of this basic operation paves the way for mastering more complex mathematical concepts and problem-solving strategies. Remember, the foundation of mathematical proficiency is built on a thorough understanding of its fundamental operations.
Latest Posts
Latest Posts
-
1 Pint Vs 1 Quart
Sep 23, 2025
-
How To Find Common Stock
Sep 23, 2025
-
Lewis Dot Structure For Icl3
Sep 23, 2025
-
Sample Texas Real Estate Exam
Sep 23, 2025
-
What Is 10 Of 45000
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 1 000 Divided By 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.